Das Wichtigste in Kürze
Ein Weg-Zeit-Diagramm (s,t-Diagramm) hat meistens als horizontale Achse die Zeitachse und als vertikale Achse die Ortskoordinate, die für eine bestimmte Position, die eine eindimensionalen Strecke definiert.
Wenn wir einen Abschnitt auf der Zeitachse meinen, dann ist das eine Zeitperiode \(\Delta t\), z.B. von 7:30 Uhr bis 8:30 Uhr, d.h. eine Stunde:
\[ \Delta t = t_2 – t_1 \]
Da die Zeitperiode als Differenz von zwei Zeitpunkten berechnet wird, schreiben wir sie mit einem \(\Delta\) (griechischer Buchstabe “Delta”, stellvertretend für “D” bzw. “Differenz”).
Wenn wir eine Strecke \(\Delta s\) meinen, dann bilden wir ebenfalls die Differenz der beiden Ortskoordinaten:
\[ \Delta s = s_2 – s_1 \]
Im s,t-Diagramm können wir eine Geschwindigkeit als Steigung ablesen, denn es gilt das Steigungsdreieck:
\[ v = \frac{\Delta s}{\Delta t} \]
Stillstand bedeutet keine Geschwindigkeit und ist im s,t-Diagramm eine Horizontale.
Nimmt die Ortskoordinate mit der Zeit ab, kriegen wir eine negative Steigung. Sie steht für eine “negative Geschwindigkeit”, die nichts anderes bedeutet als eine Bewegung zurück.
Videos
-
s-t-Diagramm – Zwei Züge (0028)
Häufigste Fragen
“Der Nullpunkt und die Richtung sind eine rein willkürliche Definitionssache, ohne physikalische Bedeutung.”
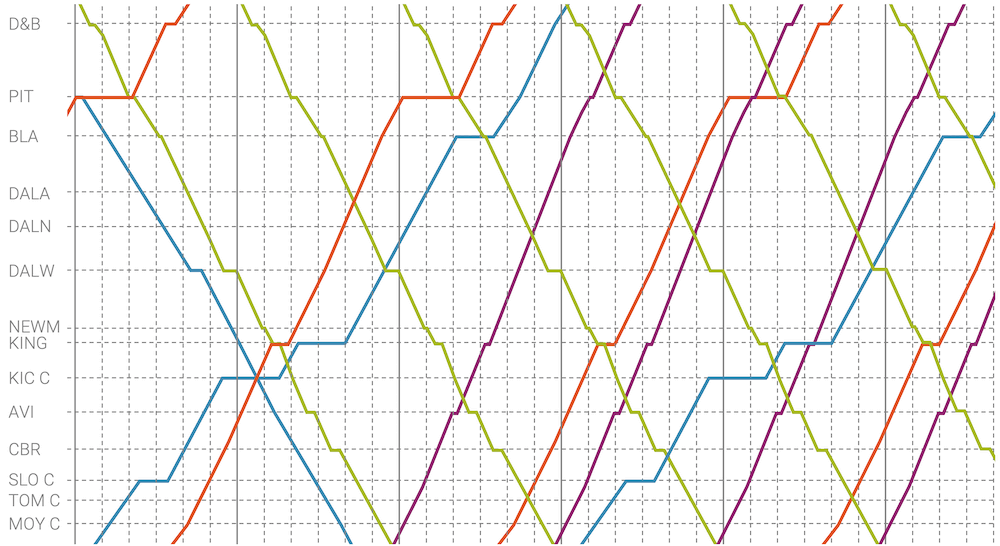
In einem s,t-Diagramm oder Weg-Zeit-Diagramm wird eine Position (\(s\)-Koordinate) über die Zeit \(t\) aufgetragen. Die Darstellung ist nützlich, um eine eindimensionale Bewegung zu beschreiben oder Aussagen über diese Bewegung machen zu können.
Beispielsweise kann die Geschwindigkeit als Steigung im s,t-Diagramm oder die Beschleunigung als Krümmung abgelesen werden. Das s,t-Diagramm zeigt uns aber auch Haltepausen, die Richtung der Bewegung, Kreuzungsorte oder -zeitpunkte etc.
Weg-Zeit-Diagramme werden als “Bildfahrpläne” beispielsweise in der Disposition von Zügen oder Bussen eingesetzt. Üblicherweise wird die Zeit auf der horizontalen Achse und die Position \(s\) auf der eindimensionalen Strecke auf der vertikalen Achse aufgetragen.
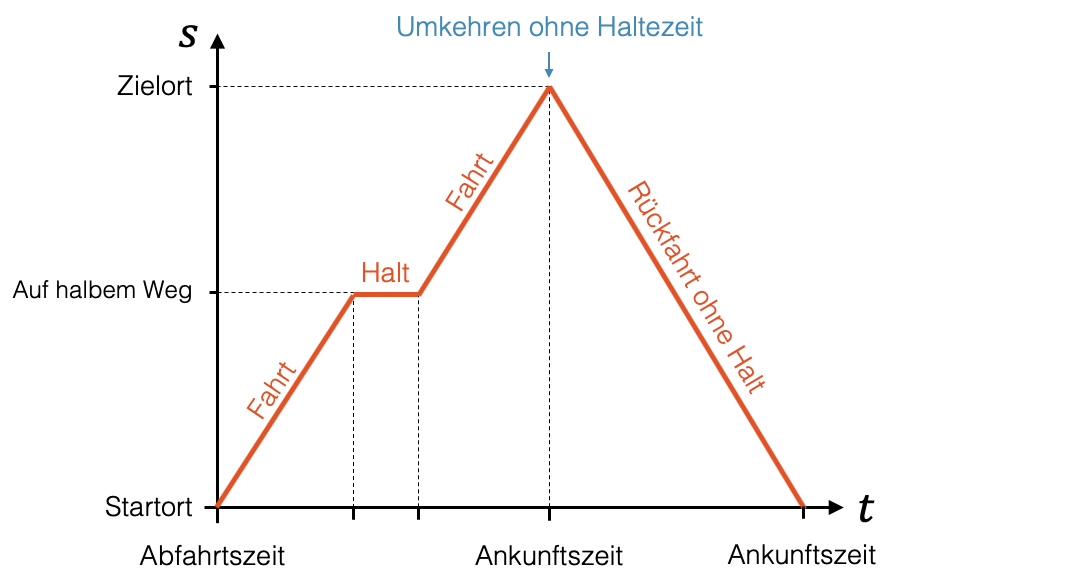
Wichtigste Grundmuster:
- Vorwärtsbewegung (langsam): von links unten nach rechts oben, leicht steigend (relativ flach)
- Vorwärtsbewegung (schnell): von links unten nach rechts oben, stark steigend (steil)
- Halt: horizontaler Verlauf (\(t\) nimmt zu, \(s\) bleibt gleich)
- Rückfahrt: von links oben nach rechts unten
Die Strecke gilt als eindimensional, weil sie durch eine einzige Dimension, dem Parameter \(s\) beschrieben ist.
Wir müssen sie als Ortskoordinate verstehen. Wenn wir beispielsweise den Kilometer 14 auf einer definierten Route meinen, so ist der Ort klar definiert. Wir können an diesem Ort auch einen “Kilometerstein” aufstellen.
Natürlich bewegt sich die Route selber im dreidimensionalen Raum, d.h. mal nach links, dann nach rechts, mal hoch, mal runter. Da die Bewegung aber an der Strasse oder Schiene gebunden ist, können wir uns nur entlang der Strasse/Schiene in einer Dimension uns bewegen:
- vorwärts (Ortskoordinate nimmt im Wert zu)
- rückwärts (Ortskoordinate nimmt im Wert ab)
- Halt/Stillstand (Ortskoordinate bleibt konstant)
Eine andere Bewegung als vorwärts/Halt/rückwärts ist im eindimensionalen Fall mit der einen Dimension \(s\) nicht erlaubt. Wir müssten eine weitere, zweite Dimension einführen.
Beachte auch, dass der Nullpunkt und die Richtung auf der Strasse oder Schiene, eine rein willkürliche Definitionssache ist. Wir sind frei diese Definition vorzunehmen und zu sagen, was für die Bewegung definitionsgemäss vorwärts sein soll, d.h. in welcher Richtung \(s\) zunehmen wird.
Diese Definition hat keine physikalische Bedeutung, d.h. die Physik der Bewegung kann mit verschiedenen s,t-Diagrammen beschrieben werden, ohne dass sich die Bewegung ändert.
Beispiel: Zeichnen eines s,t-Diagramms
Ein Schnellzug fährt von Zürich nach St. Gallen mit dem folgenden Fahrplan. Wie sieht das s,t-Diagramm aus?
| Bhf | Zürich | Flughafen | Winterthur | St. Gallen |
| an | 18:42 | 18:57 | 19:35 | |
| ab | 18:33 | 18:44 | 18:59 |
So sieht das vereinfachte s,t-Diagramm dazu aus. Natürlich kennen wir den genauen Geschwindigkeitsverlauf über die Zeit nicht. Wir haben deshalb die Geschwindigkeit jeweils konstant angenommen (konstante Steigung zwischen zwei Bahnhöfen).
Wir sehen, dass der Zug offenbar zwischen Winterthur und St. Gallen im Schnitt schneller unterwegs ist, als etwa zwischen Zürich und dem Flughafen. Wir können auch die Haltezeiten von den Fahrzeiten gut unterscheiden.
Aufgabensammlung
-
Zwei Züge (0028)
4 Teilaufgaben mit Lösungen (pdf/Video):
• Weg-Zeit-Diagramm aufstellen
• Zeitpunkt und Ort bestimmen
Lernziele
- Du weisst, wie ein s,t-Diagramm gezeichnet wird und wie der Verlauf einer Bewegung “gelesen” wird.
- Du verstehst, wie ”vorwärts” und ”rückwärts” zu verstehen sind und warum es sich um eine eindimensionale Bewegung handelt, auch wenn sie im 3-dimensionalen Raum stattfindet.
Weitere Links
Bildfahrplan (Wikipedia)
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.