Bewegungsgleichungen

Warum braucht es Bewegungsgleichungen?

Wir machen ein Beispiel: Wie lange ist die benötigte Strecke für eine Beschleunigung von 10 m/s auf 30 m/s in 5 Sekunden? Diese Aufgabe wird durch den Umstand erschwert, dass die Geschwindigkeit sich verändert, wir also eine Bewegung mit Beschleunigung haben.

Am besten machen wir uns schnell ein v-t-Diagramm, um den Verlauf der Geschwindigkeit zu erfassen.

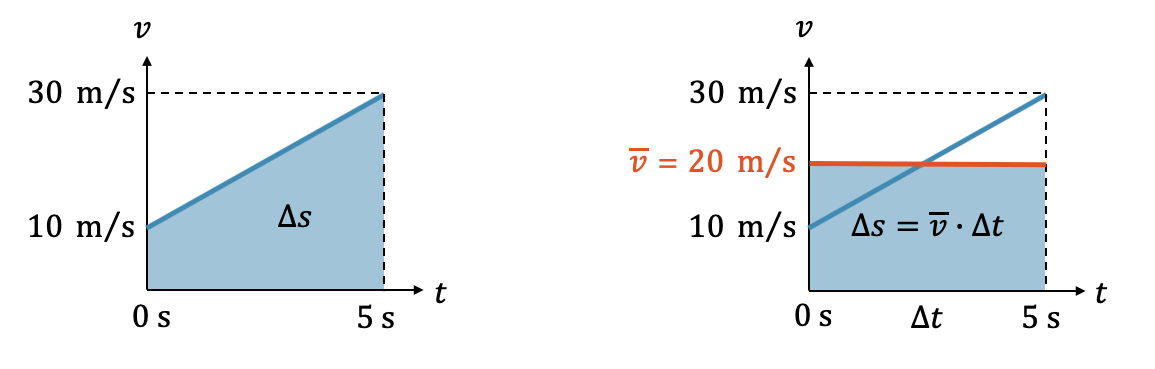
Wir erinnern uns an die Tatsache, dass in einem v-t-Diagramm, wir die Strecke \(\Delta s\) als Fläche ablesen können. Gesucht ist also die Fläche des Trapezes. Wir können diese Fläche als Kombination eines Rechtecks mit Höhe 10 m/s und eines Dreiecks mit Höhe 20 m/s erhalten.

Noch etwas eleganter ist die Umwandlung der Trapezfläche in eine gleich grosse Rechteckfläche der Höhe 20 m/s. Wir kriegen so:

\[ 20\,\frac{\text{m}}{\text{s}} \cdot 5\,\text{s} = \underline{100\,\text{m}} \]

Für die Beschleunigung sind 100 m nötig. 👍

Für die Berechnung haben wir hier einen Umweg über das v-t-Diagramm gemacht und uns überlegt, wie wir diese Fläche berechnen können. Mit den Bewegungsgleichungen geschieht dieser Ablauf automatisch im Hintergrund. Wir benutzen dazu eine Art “Kochrezept”:

1. Alle Grössen aufschreiben, die gegeben sind, eventuell eine Skizze machen (meistens sind \(s_0\) und \(v_0\) indirekt gegeben)
2. Was ist die gesuchte Grösse?
3. Welche Bewegungsgleichung passt? (Habe ich nur eine Unbekannte, nämlich die gesuchte Grösse?)
4. Bewegungsgleichung nach der gesuchten Grösse auflösen (Algebra)
5. Gegebene Werte einsetzen, Ausrechnen, Einheiten nicht vergessen (Kontrolle: entspricht die Einheit der Aufgabenstellung?)

Schritt 1: In unserem Beispiel sind die gegeben Grössen die Folgenden:

\[ s_0 = 0\,\mathrm{m}, \quad v_0 = 10\,\frac{\mathrm{m}}{\mathrm{s}}, \quad v_1 = 30\,\frac{\mathrm{m}}{\mathrm{s}} \]

Beachte, dass in vielen Textaufgaben gewisse Angaben in Textform versteckt sind. Beispielsweise bedeutet “…aus der Ruhe heraus” die versteckte Angabe \(v_0=0\).

Schritt 2: Die gesuchte Grösse ist \(s_1\).

Schritt 3: Im Satz von Bewegungsgleichungen wählen wir die Gleichung (2), weil in ihr nur die bekannten Grössen \(s_0, v_0\) und \(v_1\) und die gesuchte Grösse \(s_1\) vorkommen. Wir haben damit eine Gleichung mit einer Unbekannten, d.h. sie ist für die Unbekannte \(s_1\) lösbar.

\[ s_1 = s_0 + \frac{1}{2} (v_0 + v_1) \Delta t \qquad \text{(2)} \]

Schritt 4: Da die Gleichung schon nach \(s_1\) aufgelöst ist, entfällt die Algebra

Schritt 5: Wir können direkt die Werte einsetzen:

\[ s_1 = 0 + \frac{1}{2} \cdot \Big(10\,\frac{\mathrm{m}}{\mathrm{s}} + 30\,\frac{\mathrm{m}}{\mathrm{s}}\Big) \cdot 5\,\text{s} = \underline{100\,\text{m}} \]

Je nach Aufgabenstellung wählst du die passende Bewegungsgleichung, die die Grössen der Aufgabenstellung enthält, bis auf die gesuchte Grösse. Damit erhältst du eine Gleichung mit einer Unbekannten.

Verwendung der mittleren Geschwindigkeit

Im obigen Beispiel haben wir gesehen, dass die Trapezfläche mit Hilfe einer geschickten Umwandlung in eine einfach zu berechnende Rechtecksfläche umgewandelt werden kann.

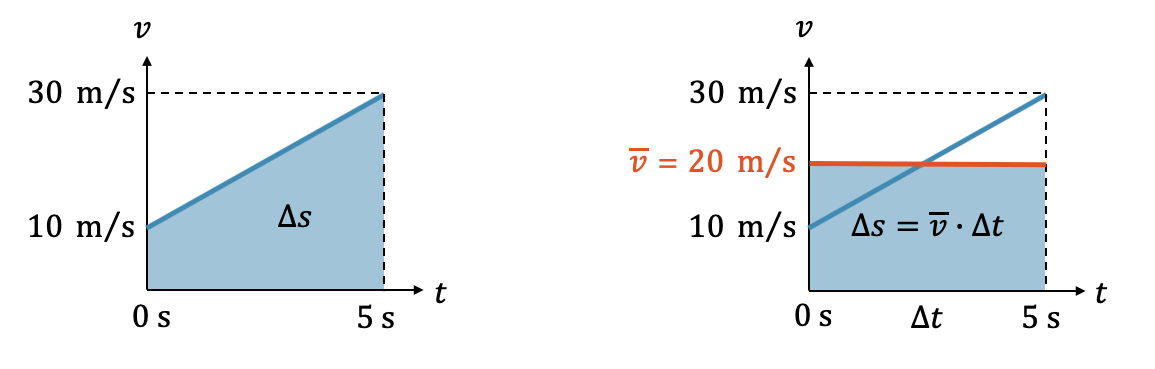
Die Höhe des Rechtecks im Diagramm muss genau so gewählt werden, dass das Rechteck die gleiche Fläche wie das Trapez hat.

Wir sehen im Bild, dass die beiden kleinen rechtwinkligen Dreiecke gleich gross sein müssen und dass damit die rote Linie genau auf mittlerer Höhe platziert werden muss. Diese Höhe entspricht der mittleren Geschwindigkeit \(\overline{v}\) im betrachteten Zeitraum.

Fazit: Wir können Aufgaben mit Beschleunigungen immer stark vereinfachen, wenn wir die mittlere Geschwindigkeit berechnen, denn diese bleibt über die betrachtete Zeitperiode konstant. Wenn eine Geschwindigkeit konstant bleibt, fällt die Beschleunigung weg! Keine Beschleunigung mehr – einfache Rechnung!

Der Rechenweg könnte also folgendermassen gehen:

Die Geschwindigkeit ändert sich gleichmässig von 10 m/s auf 30 m/s, d.h. wir haben eine mittlere Geschwindigkeit von 20 m/s. Wir fahren mit dieser mittleren Geschwindigkeit während 5 s, d.h. wir fahren eine Strecke von:

\[ \overline{v} = \frac{\Delta s}{\Delta t} \quad \rightarrow \quad \Delta s = \overline{v} \cdot \Delta t\]

\[ \Delta s = 20\;\frac{\text{m}}{\text{s}} \cdot 5\,\text{s} = \underline{100\,\text{m}} \]

Das ist vermutlich der einfachste Weg! 😎

Herleitung der Bewegungsgleichung (1)

Wir werden die oben beschriebene Trapezfläche nehmen und daraus die Bewegungsgleichung (1) herleiten.

Die Fläche im v-t-Diagramm entspricht der gefahrenen Strecke: \(\Delta s \;=\; s_1 – s_0\)

Das Trapez betrachten wir als Rechteckfläche (Höhe \(v_0\)) + Dreiecksfläche mit Höhe \(\Delta v = (v_1-v_0)\). Beide haben die Breite \(\Delta t\).

Somit gilt für ganze Fläche bzw. gefahrene Strecke:

\[ \Delta s = v_0 \Delta t + \frac{1}{2} \Delta v \Delta t  \]

Wir benutzen jetzt die Definition der Beschleunigung \(a = \frac{\Delta v}{\Delta t}\) und lösen nach \(\Delta v\) auf. Wir kriegen \(\Delta v = a \cdot \Delta t\) und setzen das oben ein. Ausserdem ersetzen wir \(\Delta s = s_1 – s_0\).

\[ s_1 – s_0 = v_0 \Delta t + \frac{1}{2} a \Delta t^2  \]

Jetzt addieren wir nur noch die Gleichung mit \(s_0\) und erhalten die Bewegungsgleichung (1):

\[ s_1 = s_0 + v_0 \Delta t + \frac{1}{2} a \Delta t^2 \qquad \text{(1)} \]

Wir sehen damit, dass die Bewegungsgleichung nichts anderes ist, als die korrekte Berechnung der Fläche im v-t-Diagramm unter Berücksichtigung der sich verändernden Geschwindigkeit \(v(t)\).