Videos

Image by Marcin Białek, licensed under CC BY 4.0
Kraft des elektrischen und des magnetischen Felds
Eine elektrische Ladung \(q\) erfährt in einem elektrischen Feld \(\vec{E}\) eine Coulombkraft und wird dadurch beschleunigt:
\[ \vec{F}_C = q \cdot \vec{E} \]
Tritt eine elektrische Ladung in ein Magnetfeld \(\vec{B}\), so wird auch hier eine Kraft auf sie wirken. Es handelt sich dieses Mal aber um eine seitliche Kraft, die die Ladung umlenkt. Die Ladung behält den Betrag ihrer Geschwindigkeit \(\vec{v}\) bei, d.h. sie wird durch die Kraft aufgrund des magnetischen Felds weder schneller, noch langsamer. Sie ändert aber die Richtung ihrer Geschwindigkeit.
\[ \vec{F}_M = q \cdot \big( \vec{v} \times \vec{B} \big) \]
Die Summe der beiden Kräfte vom elektrischen und vom magnetischen Feld ergibt die totale Kraft, die auf die Ladung wirkt. Diese Summe heisst Lorentzkraft und ist benannt nach dem niederländischen Physiker Hendrik Lorentz (1853 – 1928), der unter anderem auch mit dieser Kraft die mathematischen Grundlagen für Einsteins Spezielle Relativitätstheorie legte:
Lorentzkraft
\[ \vec{F} = q \cdot \vec{E} \; + \; q \cdot \big( \vec{v} \times \vec{B} \big) \]
Der erste Summand (1. Teilkraft) ist die Coulombkraft auf die Ladung aufgrund des E-Felds. Sie kann die Ladung beschleunigen oder abbremsen.
Der zweite Summand (2. Teilkraft) ist die Kraft aufgrund des B-Felds. Weil diese senkrecht zur Bewegungsrichtung wirkt, kann sie die Ladung nicht beschleunigen oder abbremsen, aber sie kann sie umlenken im Sinne einer Zentripetalkraft.
Wir werden uns im weiteren auf den Einfluss des Magnetfelds beschränken und nur die Teilkraft anschauen, die vom Magnetfeld herrührt:
\[ \vec{F} = q \cdot \big( \vec{v} \times \vec{B} \big) \]
Kraft auf einen mit Strom durchflossenen Leiter
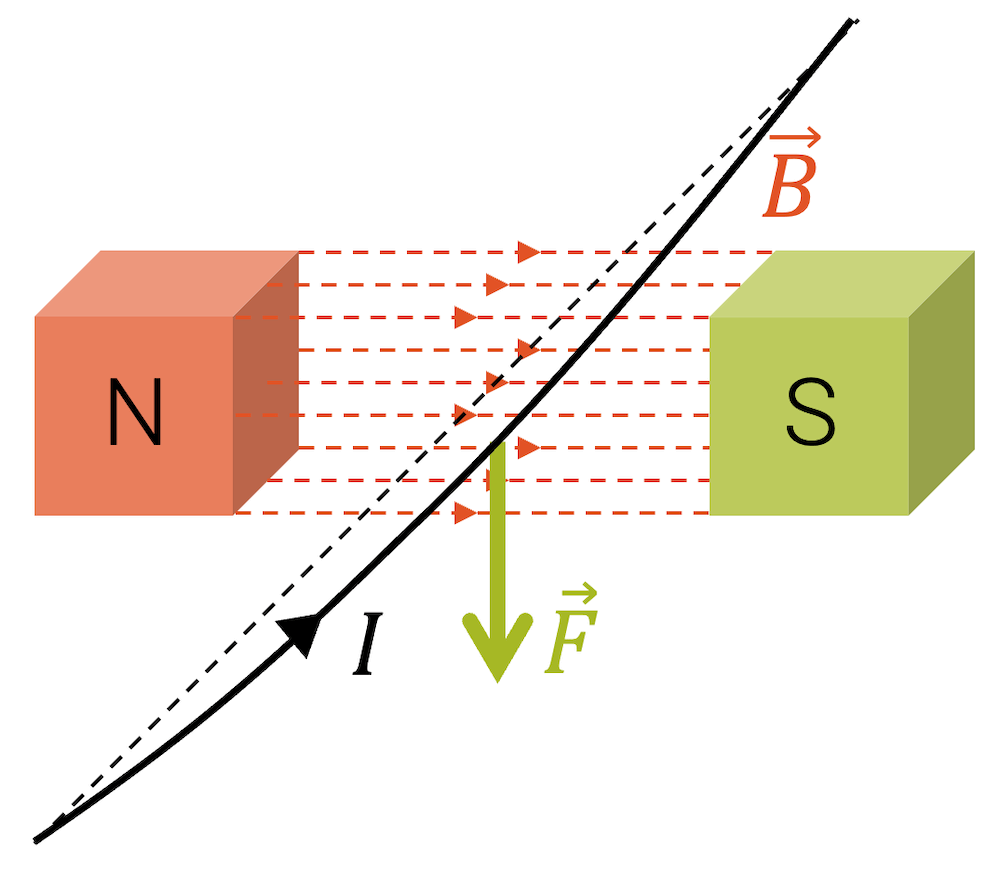
Im nachfolgenden Bild sehen wir, wie eine Lorentzkraft auf einen Leiter wirkt, der mit Strom durchflossen wird und durch ein Magnetfeld führt. Fliesst kein Strom, so wirkt auch keine Lorentzkraft. Jedes Mal beim Schliessen des Schalters, werden wir eine leichte Bewegung des Leiters nach oben beobachten können.
Die Lorenzkraft wirkt eigentlich auf die Ladungsträger, d.h. auf die Elektronen und nicht auf den Leiter selbst, aber die Ladungsträger ziehen den Leiter mit, so dass wir beobachten können, wie ein Leiter sich bewegt, sobald er mit Strom durchflossen wird.
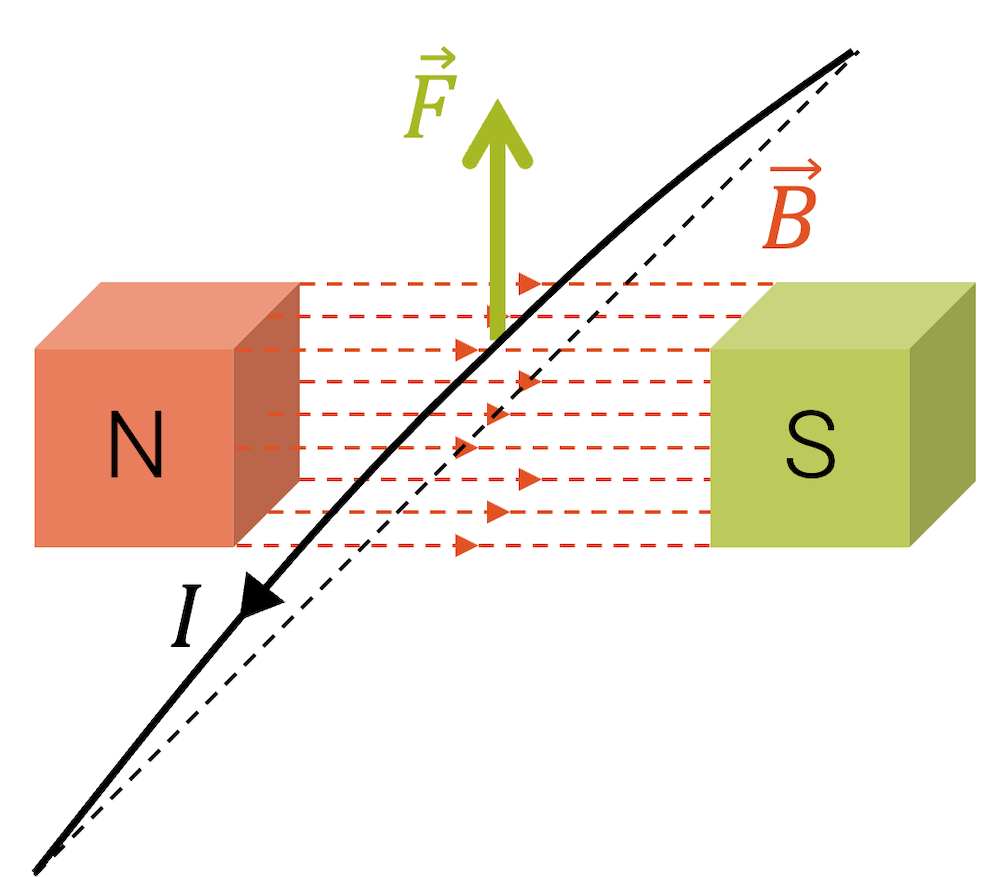
Wenn wir die Richtung des Stroms umkehren, wirkt die Lorenzkraft in die andere Richtung. Ein Umpolen des Magnetfelds führt ebenfalls zu einer Richtungsänderung der Lorentzkraft. Die Lorentzkraft wirkt immer senkrecht zur Bewegungsrichtung der Ladungsträger.
Egal, ob Elektronen sich frei bewegen oder in einem Leiter sich bewegen; sie erfahren immer eine Lorentzkraft, sobald sie sich in einem Magnetfeld bewegen. Damit die Lorentzkraft auftritt braucht es die Bewegung der Ladung (\(\vec{v}\)) und ein Magnetfeld (\(\vec{B}\)).
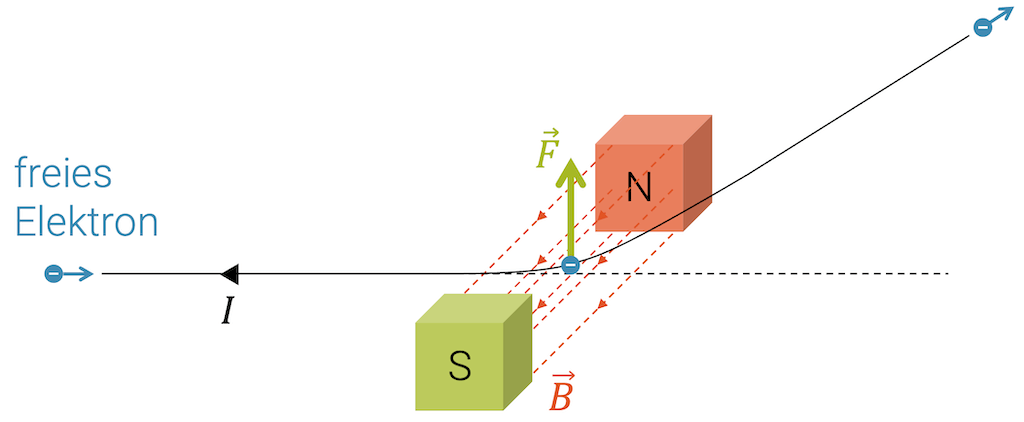
Im nachfolgenden Beispiel wird ein freies Elektron im Magnetfeld von der Lorentzkraft umgelenkt, so dass es danach auf einer geraden Linie, jedoch etwas nach oben weiterfliegt.
Beachte, dass die Bewegungsrichtung des Elektrons (blauer Pfeil) der Richtung des technischen Stroms (schwarzer Pfeil) entgegengesetzt ist. Der technische Strom zeigt ja die Flussrichtung positiver Ladung an. Für die Lorentzkraft ist es wichtig, dass wir für die Geschwindigkeit \(\vec{v}\) diejenige der positiven Ladung nehmen, also gerade der Bewegungsrichtung des negativen Elektrons entgegengesetzt.
Aus allen Beispielen, die wir bis hierher gesehen haben, können wir für das Kreuzprodukt von \(\vec{v}\) und \(\vec{B}\) die folgende Rechte-Hand-Regel verwenden:
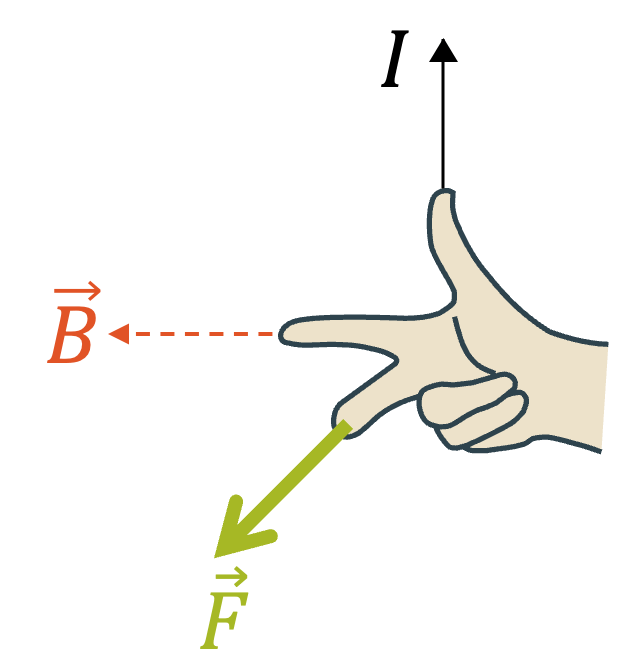
Rechte-Hand-Regel für die Bestimmung der Richtung der Lorentzkraft (Anteil magnetisches Feld):
- Daumen in Richtung der positiven Ladung (Geschwindigkeit \(\vec{v}\) bzw. technischer Strom \(I\))
(Beachte: Für negative Ladungen ist die entgegengesetzte Richtung zu nehmen) - Zeigefinger in Richtung des magnetischen Felds \(\vec{B}\)
Der Mittelfinger zeigt uns dann die Richtung der wirkenden Lorentzkraft.
Kraft zwischen zwei Leitern
André-Marie Ampère (1775-1836) war ein französischer Physiker und Mathematiker. Im Jahre 1820 zeigte er im Experiment, dass zwei parallele Leiter, die je einen gleich gerichteten Strom führten, sich gegenseitig anziehen würden. Wenn die beiden Leiter Ströme in entgegengesetzter Richtung führen, wirkt eine abstossende Kraft auf beide Leiter.
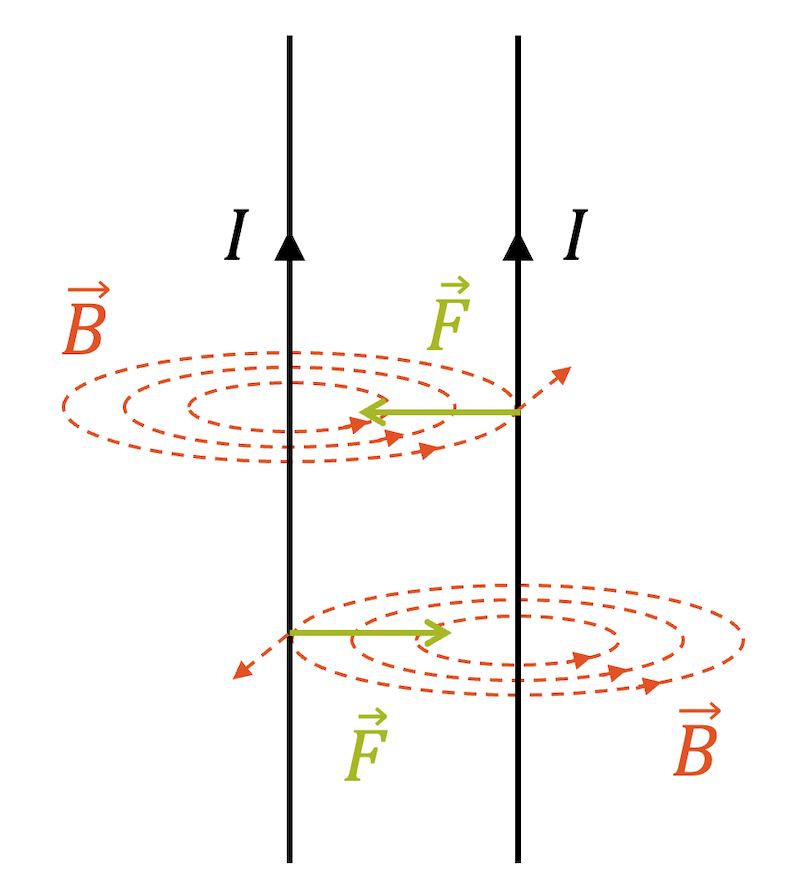
Schauen wir uns den linken Leiter als Erstes an: Er führt einen Strom von unten nach oben. Wir wissen, dass der elektrische Stom in einem Leiter ein Magnetfeld erzeugt, das kreisförmig um den Leiter herum zeigt. Mit der Rechten-Hand-Regel setzen wir den Daumen nach oben (in Stromrichtung) und erhalten mit den restlichen Fingern die Richtung des kreisförmigen Magnetfelds im Gegenuhrzeigersinn, wenn wir von oben herabschauen.
Jetzt betrachten wir die Richtung dieses Magnetfelds im anderen Leiter: Es zeigt nach hinten. Wenn in diesem zweiten Leiter ebenfalls ein Strom nach oben führt und dabei in das Magnetfeld des ersten Leiters gelangt, wirkt eine Lorentzkraft nach links. Die Betrachtung gilt in gleicher Weise auf alle Punkte im zweiten Leiter, d.h. der ganze Leiter erfährt eine Lorentzkraft nach links.
Analog bewirkt der Strom im zweiten Leiter (rechts) ein kreisförmiges Magnetfeld, welches im ersten Leiter zu einer Lorentzkraft führt, die dieses Mal nach rechts zeigt.
Führen die beiden Leiter zwei einander entgegengerichtete Ströme, so sind die beiden Lorentzkräfte einander entgegengesetzt nach aussen, d.h. sie drücken die beiden Leiter auseinander.
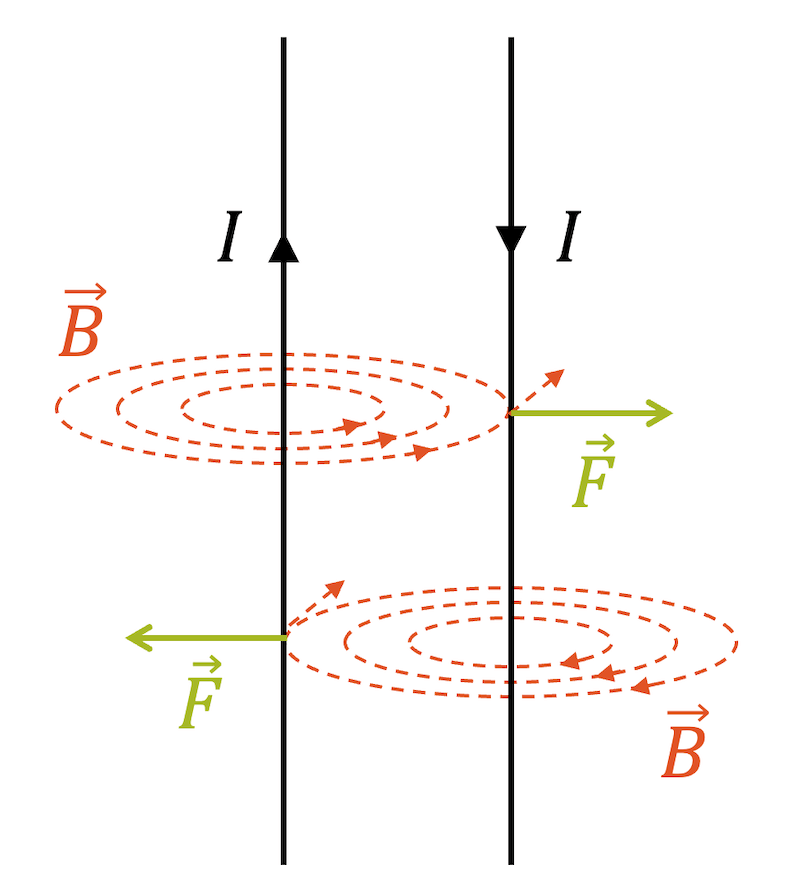
Zwei parallele Leiter ziehen sich gegenseitig an (Lorentzkraft), wenn ihr Strom gleich gerichtet ist. Wenn ihre Ströme entgegengesetzt sind, stossen sie sich ab.
Untersuchung von radioaktiver Strahlung
Werden verschiedene Arten von radioaktiver Strahlung durch ein Magnetfeld geschickt, können wir die Strahlungsarten an aufgrund ihrer Auslenkung von einander unterscheiden. Radioaktive Strahlung kommt im wesentlichen auf drei Arten vor:
- Alpha-Strahlung besteht aus Alpha-Teilchen, die aus zwei Protonen und zwei Neutronen zusammengesetzt sind. Diese Teilchen sind zweifach positiv geladen
- Beta-Strahlung besteht aus hoch energetischen Elektronen, d.h. aus negativ geladenen Teilchen
- Gamma-Strahung ist hochenergetische elektromagnetische Strahlung. Sie besteht aus Photonen, die keine elektrische Ladung besitzen
Die Richtung der Lorentzkraft wird bestimmt durch die Richtung des Magnetfelds (\(\vec{B}\)) und der Bewegungsrichtung der positiven Ladung (\(\vec{v}\)):
\[ \vec{F} = q \cdot \big( \vec{v} \times \vec{B} \big) \]
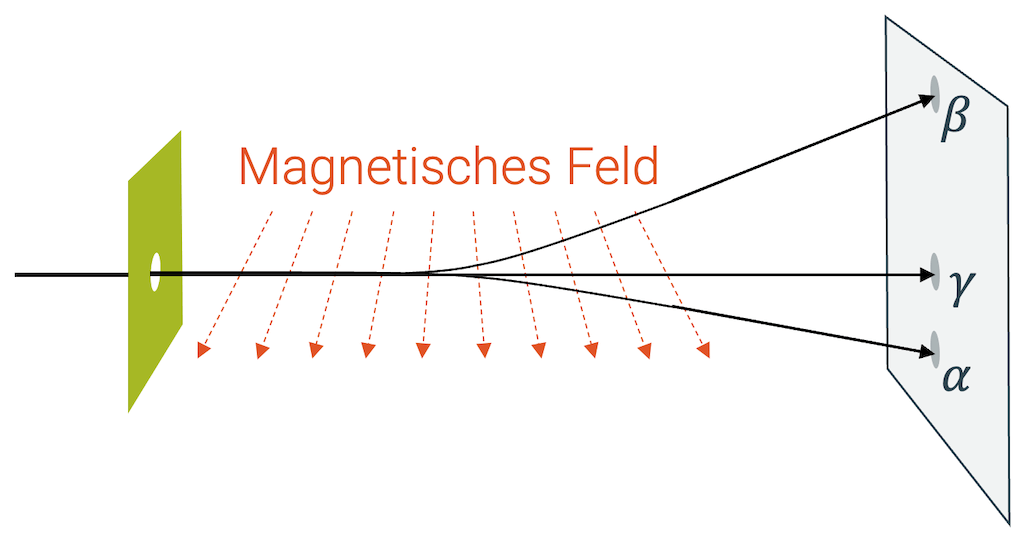
Im Falle der Alpha-Strahlung erhalten wir im folgenden Bild eine Lorentzkraft, die nach unten wirkt. Wir können dies mit der Rechte-Hand-Regel überprüfen: Der Daum zeigt nach rechts, in der Richtung der positiven Alpha-Teilchen. Das Magnetfeld zeigt aus der Zeichenebene heraus. Unser Mittelfinger zeigt in diesem Fall nach unten. Der Strahl der Alpha-Teilchen wird deshalb etwas weiter unten auf dem Detektor auftreffen.
Die negativen Elektronen der Beta-Strahlung bewegen sich nach rechts, was einer Bewegunsrichtung von positiver Ladung nach links entspricht. Dadurch zeigt die Lorentzkraft, die auf die Elektronen wirkt, nach oben und der Detektor wird ein Auftreffen der Elektronen im oberen Teil registrieren.
Die Teilchen der Gamma-Strahlung (Photonen) haben keine elektrische Ladung. Sie können deshalb auch keine Lorentzkraft verspüren. Sie fliegen (ohne Auslenkung) geradeaus nach rechts zum Detektor und treffen in der Mitte ein.
Unbekannte radioaktive Strahlung kann als Alpha-, Beta- oder Gamma-Strahlung identifiziert werden, indem die elektrische Ladung der betreffenden Teilchen, die die Strahlungsart ausmacht, mit Hilfe der Lorentzkraft unterschieden werden kann.
Massenspektrometer
Das Prinzip der Auslenkungen von Ladungen im Magnetfeld wird auch in sog. Massenspektrometern genutzt. Das sind analytische Geräte, die sagen können, welche Stoffe in einer Probe enthalten sind. Auf diese Weise können chemische Verbindungen in einer Probe nachgewiesen oder gar die ganze chemische Zusammensetzung der Probe bestimmt werden.
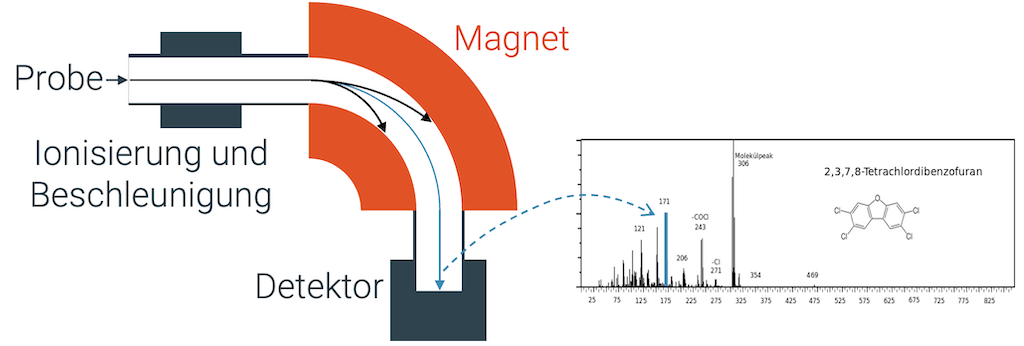
Die Materialprobe wird ionisiert, so dass geladene Ionen entstehen. Grössere Moleküle zerfallen dabei auch in Teilstücke, d.h. es werden nicht nur Elektronen vom Molekül entfernt.
Die Ionen werden in einem elektrischen Feld beschleunigt und treten dann in ein Magnetfeld ein. Die zur Bewegungsrichtung senkrecht liegende Lorentzkraft lenkt die Bahn der Ionen ab. Die Stärke der Kraft ist abhängig von der Ladung des Ions. Die Ionen selber sind aber verschieden schwer. Angenommen, die Ionen hätten alle die gleiche Ladung. In diesem Fall ist die Lorentzkraft auf alle Ionen gleich gross. Gemäss Newtons Zweitem Gesetz werden die schweren Ionen mit ihrer grossen Masse nur schwach seitlich beschleunigt, d.h. ihre Auslenkung wird schwach sein und sie fliegen einen grossen Bogen. Leichte Ionen hingegen erfahren die gleich grosse Lorentzkraft und werden seitlich stark beschleunigt, so dass sie eine viel engere Kurve fliegen.
Nur ein kleiner Bruchteil der Ionen hat die ideale Masse, so dass sie die ideale Kurve fliegen, weder zu eng, noch zu weit. Damit wird nur ein kleiner Bruchteil der Ionen den Detektor erreichen. Dieser registriert, wie viele ankommen und schickt die Information an den Computer.
Das Gerät stellt dann das Magnetfeld anders ein, z.B. leicht stärker. Jetzt ist auch die Lorentzkraft etwas stärker und alle Flugbahnen sind etwas stärker gekrümmt. Die Ionen, die vorhin die ideale Kurve geflogen sind, kollidieren an der inneren Wand und scheiden deshalb aus. Nun kommen Ionen mit ein bisschen mehr Masse beim Detektor an. Ihre Flugbahn war vorher zu weit und sie sind an der äusseren Wand ausgeschieden. Jetzt werden sie aber vom Detektor registriert und ihre Menge wird gemessen und an den Computer geschickt.
Der Massenspektrometer führt diese Messungen über das ganze Spektrum der Massen durch und kann dann sagen, welche Massen, wie oft vorgekommen sind. Aufgrund dieser Informationen kann rekonstruiert werden, welche Moleküle ursprünglich in der Probe vorhanden waren. Selbst Bruchstücke der ursprünglichen Moleküle werden vom Computer erkannt, denn sie kommen ziemlich gleich viel vor und deuten somit darauf, dass sie aus dem Zerfall eines grösseren Moleküls entstanden sind.
Mit einem Massenspektrometer werden Moleküle einer Materialprobe zu Ionen gemacht. Aufgrund der Stärke ihrer seitlichen Auslenkung durch die Lorentzkraft kann rückgefolgert werden, welche Masse diese Ionen haben. Der Detektor misst ausserdem wie viel von den betreffenden Ionen in der Probe vorhanden sind, so dass der Computer aufgrund dieser gemessenen Zusammensetzung die chemische Zusammensetzung der Probe bestimmen kann.
Aufgabensammlung
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.





Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.