Inhalt
Videos
Punkte als Elemente
Ausschnitt aus dem Kurs ‘Räumliche Vektorgeometrie 1’
Ein Punkt ist durch seine Koordinaten exakt definiert. Die Koordinaten gehören zum Punkt und bilden somit eine Einheit, die in der Mathematik Tupel genannt wird. Ein Tupel ist eine Liste von Zahlen, die zusammengehören. Die Reihenfolge spielt dabei eine wichtige Rolle. Wir können ja die \(x\)- und die \(y\)-Koordinaten nicht einfach vertauschen. Für einen Punkt \(P\) im dreidimensionalen Raum haben wir einen 3-Tupel, der wie folgt geschrieben wird:
\[ P = (P_x,P_y,P_z) \]
In ähnlicher Weise kann ein solcher Tupel auch in vier Dimensionen definiert werden, wie das z.B. in der höheren Physik üblich ist oder gar in \(n\) Dimensionen.
Wenn wir eine Gerade mit der Parameterform beschreiben, haben wir z.B. den Parameter \(\lambda\), der jeden Punkt auf der Gerade genau definiert:
\[ g \colon \;\; \begin{pmatrix} 2 \\ 3 \\ -1 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -1 \\ 1 \\ 0 \end{pmatrix} \]
Der Punkt \(P\) liegt auf der Geraden \(g\) und kann deshalb auf zwei Arten beschrieben werden, mit seinen Koordinaten, d.h. mit seinem 3-Tupel: \(P(0,5,-1)\) oder mit dem Parameterwert \(\lambda=2\). Als Element einer Menge können wir schreiben:
\[ \Big \{ (x,y,z) \;\Big|\; (0,5,-1) \Big \} \quad \text{bzw.} \quad \Big \{ \lambda \;\Big|\; 2 \Big \} \]
Das Element ist eindeutig definiert. In Kurzform schreiben wir einfach:
\[ \Big \{ (0,5,-1) \Big \} \quad \text{bzw.} \quad \Big \{ 2 \Big \} \]
Bei mehreren Punkten bzw. Elementen in der Menge, schreiben wir beispielsweise:
\[ \Big \{ (1,4,-1), \; (0,5,-1) \Big \} \quad \text{bzw.} \quad \Big \{ 1, 2 \Big \} \]
Punkte sind die Elemente, die durch ein 2- oder 3-Tupel ihrer Koordinaten eindeutig beschrieben sind. Haben wir eine Gleichung einer Geraden, einer Ebene, eines Kreises oder einer Kugel, so können Punkte auch mit einem oder zwei Parametern eindeutig beschrieben sein.
Geraden und Ebenen als Mengen
Ausschnitt aus dem Kurs ‘Räumliche Vektorgeometrie 1’
Eine Gerade kann als Reihe von Punkten betrachtet werden. Die Punkte sind unendlich in ihrer Zahl und unendlich eng zusammen, was wir natürlich nur annähernd darstellen können:
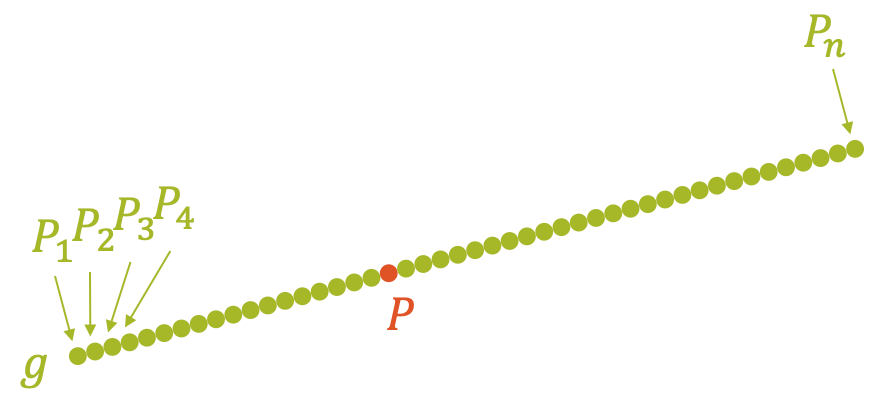
Die Gerade \(g\) kann deshalb als Menge mit unendlich vielen Punkten geschrieben werden:
\[ g = \Big\{ … , P_1, P_2, P_3, P_4, … , P_n , … \Big\} \]
Ein bestimmter Punkt \(P\), der auf der Geraden \(g\) liegt, ist dann Element dieser Menge \(g\):
\[ P \in g \]
In gleicher Weise können wir eine Ebene als unendliche Menge von Punkten betrachten:
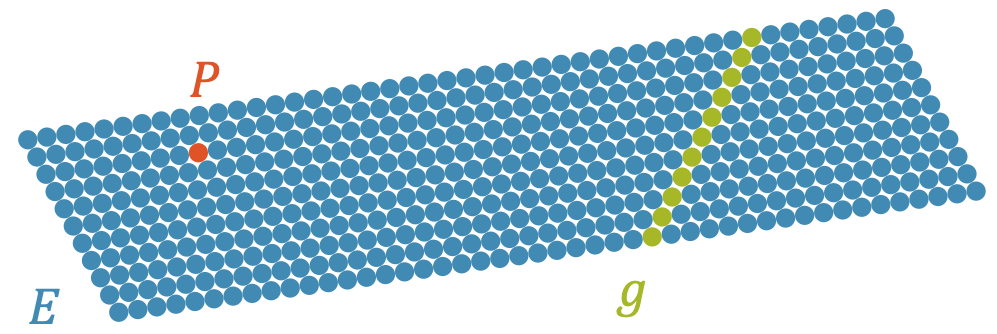
Punkte sind Elemente von Mengen, wie Geraden oder Ebenen:
\[ P \in E \]
Geraden, Ebenen, Kreise und Kugeln sind selber Mengen von Punkten, können aber Teilmengen einer grösseren Menge sein. Beispielsweise ist eine Gerade \(g\), die in der Ebene \(E\) verläuft, eine Teilmenge von \(E\):
\[ g \subset E \]
Schnittmengen
Ausschnitt aus dem Kurs ‘Räumliche Vektorgeometrie 1’
Unter einer Schnittmenge verstehen wir die gemeinsame Teilmenge von zwei Mengen, wenn diese “geschnitten” werden:
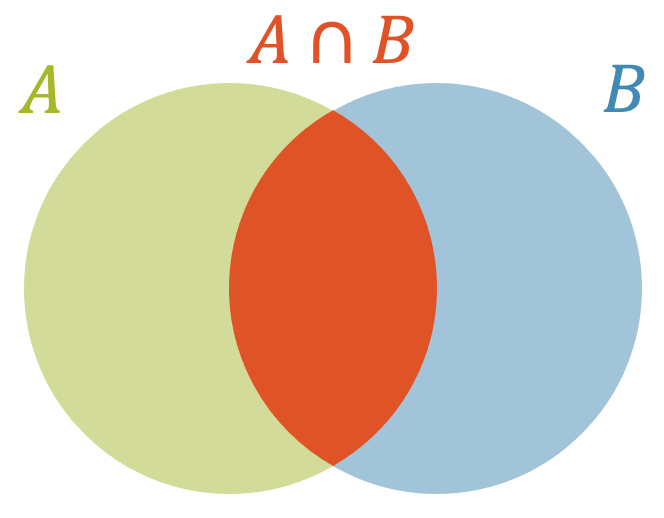
Wenn wir beispielsweise eine Ebene mit einer Geraden durchstossen, haben einen gemeinsamen Durchstosspunkt \(P\) als einziges Element in der Schnittmenge. Wenn wir zwei Ebenen miteinander schneiden, erhalten wir eine Teilmenge in Form einer Schnittgeraden und wenn wir eine Kugelfläche mit einer Geraden schneiden, erhalten wir eine Schnittmenge mit zwei Elementen \(P_1\) und \(P_2\).
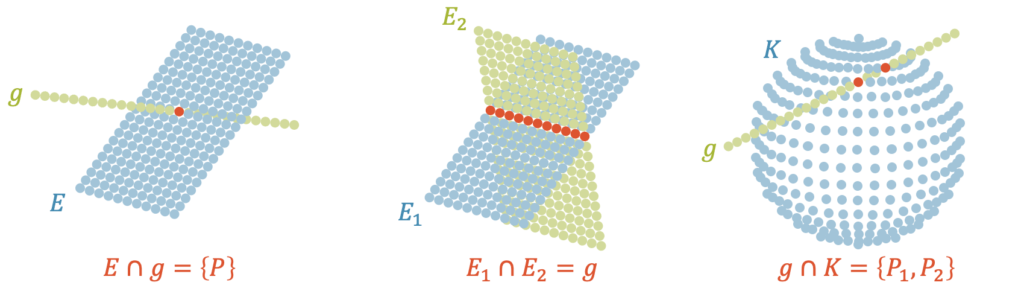
Hier gibt es aber auch Spezialfälle. Wenn die Gerade parallel ist zur Ebene, dann ist die Schnittmenge eine leere Menge, denn kein Element erfüllt diese Bedingung. Wir haben keinen Punkt in der Schnittmenge oder z.B. auch keinen Parameterwert \(\lambda\), der dies erfüllen kann.
Ein anderer Spezialfall ist beispielsweise, wenn eine Ebene eine Kugel gerade berührt. In so einem Fall erfüllt nur gerade ein Punkt die Bedingung der Schnittmenge. Wird die Ebene etwas verschoben, so erhalten wir eine Kreislinie mit unendlich vielen Punkten in der Schnittmenge oder eine leere Menge, wenn wir uns von der Kugel weg bewegen.
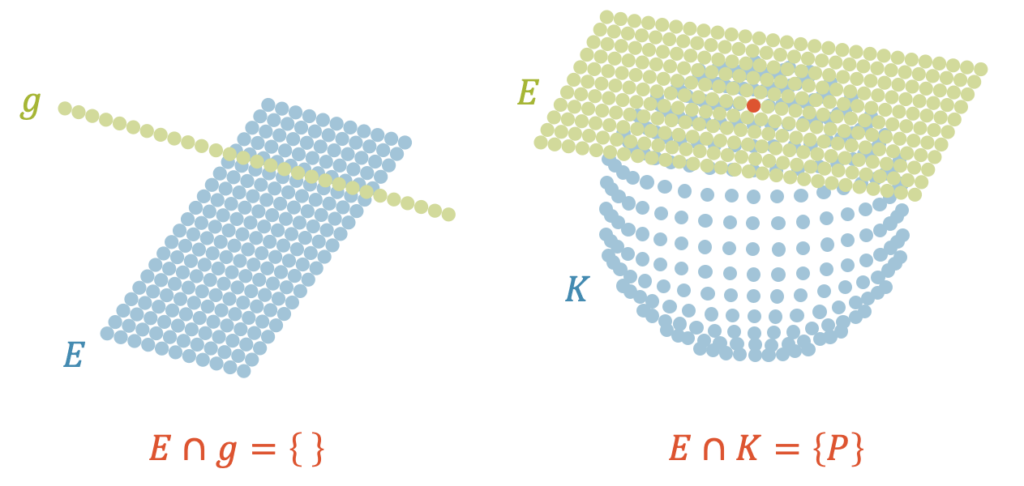
Geraden, Ebenen, Kreise und Kugeln sind Mengen von unendlich vielen Punkten, die unendlich dicht zusammenliegen. Schneiden wir diese Mengen miteinander, erhalten wir Schnittmengen, die einzelne Punkte, ganze Geraden oder einen Kreis beinhalten können. Schnittmengen können auch leer sein.
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt








Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.