Videos
Der Kathetensatz ist der dritte Satz in der Satzgruppe des Pythagoras. Er stellt eine Beziehung her zwischen einer Kathete und ihrem zugehörigen Streckenabschnitt \(p\) bzw. \(q\) auf der Hypotenuse.
Kathetensatz: Das Quadrat der Kathete \(a\) entspricht dem Produkt der Hypotenuse \(c\) und dem entsprechenden Streckenabschnitt auf der Hypotenuse:
\[a^2 = p \cdot c \]
\[b^2 = q \cdot c \]
Wir können den Kathetensatz wieder mit Quadratsflächen, dieses Mal der Katheten und den zugehörigen Rechteckflächen unterhalb der Hypotenuse darstellen. Die Länge der Rechtecke nach unten ist die nach unten geklappte ganze Hypotenuse, d.h. eigentlich ist es das Quadrat mit der Fläche \(c^2\), das durch die Verlängerung der Höhe in zwei Rechtecke aufgeteilt wird.
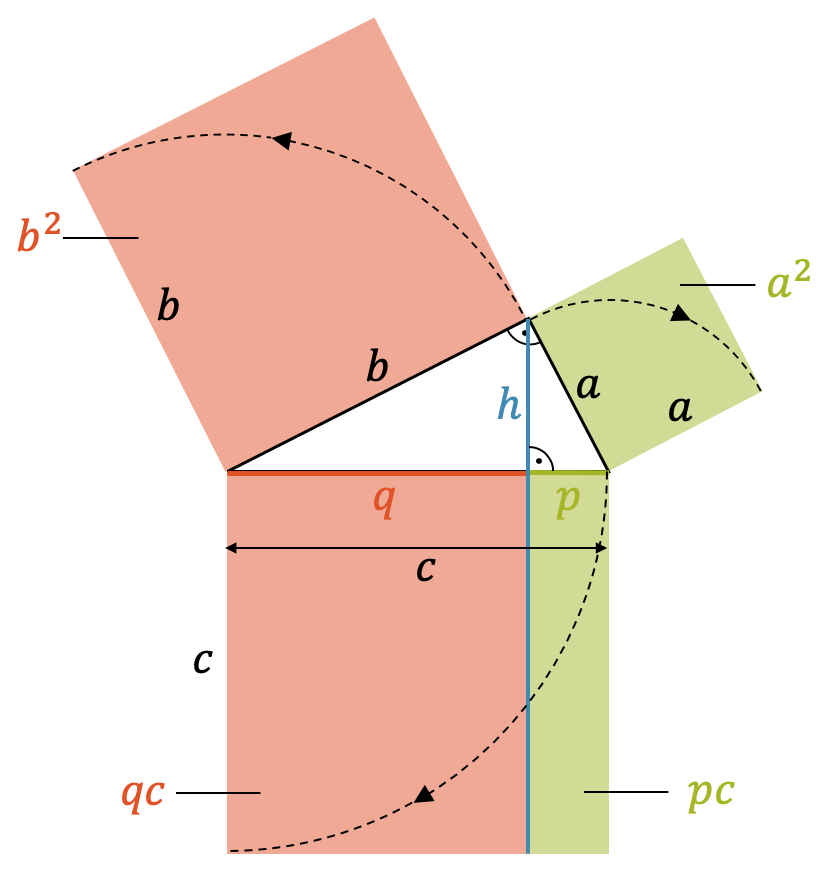
Beweis
Der Satz des Pythagoras kann nach \(a^2\) aufgelöst werden:
\[a^2 = c^2 – b^2 \]
Die Hypotenuse setzt sich aus den beiden Teilen \(p\) und \(q\) zusammen. Wir setzen deshalb \(c = p + q\).
\[a^2 = (p + q)^2 – b^2 \]
Dann ersetzen wir \(b^2\) mit einem Ausdruck mit \(q\) und \(h\). Wir benutzen dafür den Satz des Pythagoras für das linke Teildreieck: \(q^2 + h^2 = b^2\)
\[a^2 = (p + q)^2 – (q^2 + h^2) \]
\[ \require{cancel} a^2 = p^2 + 2pq + \cancel{q^2} – \cancel{q^2} – h^2 \]
Nun schauen wir uns das rechte Teildreieck an und setzen den Satz des Pythagoras auf: \(h^2 + p^2 = a^2\) bzw. \(h^2 = a^2 – p^2\). Wir ersetzen \(h^2\) mit dem neuen Ausdruck.
\[a^2 = p^2 + 2pq – (a^2 – p^2) \]
\[a^2 = p^2 + 2pq – a^2 + p^2 \]
Schliesslich können wir zusammenfassen, \(2p\) ausklammern und \((p+q)\) mit \(c\) ersetzen:
\[2a^2 = 2p^2 + 2pq = 2p \cdot (p + q) = 2pc \]
Wir erhalten somit den Kathetensatz für \(a\):
\[a^2 = pc \]
Der Kathetensatz für \(b\) wird auf die gleiche Art hergeleitet oder mit Pythagoras erhalten:
\[a^2 + b^2 = c^2 \quad \rightarrow \quad b^2 = c^2 – a^2 \]
Jetzt setzen wir den vorhin bewiesenen Kathetensatz für \(a^2\) ein benutze wieder den Umstand, dass \(p+q = c\) ist:
\[b^2 = c^2 – pc = c \cdot (c – p) = c \cdot q = qc \]
Beispiel
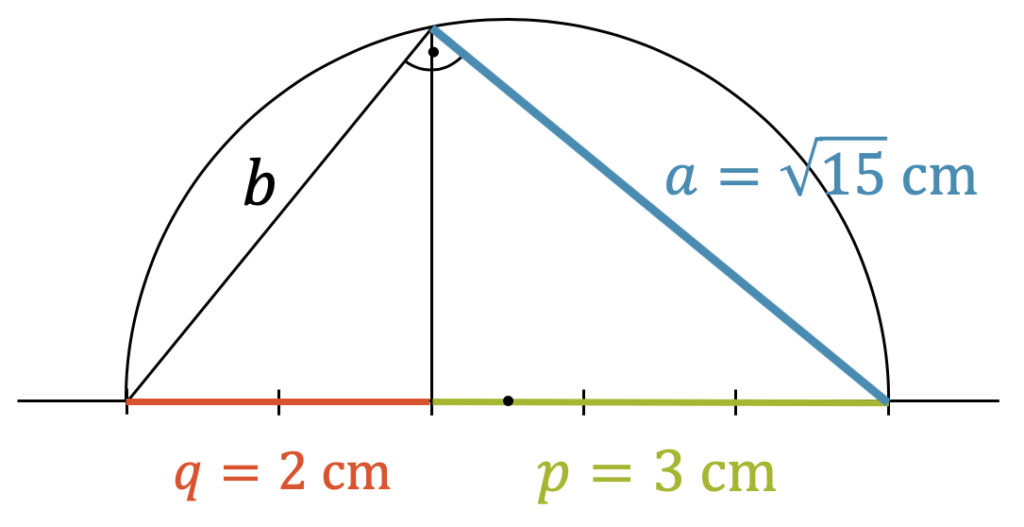
Konstruiere die Strecke \(\sqrt{15}\,\text{cm}\) mit dem Kathetensatz.
Wir schreiben den einen Kathetensatz auf:
\[a^2 = pc \]
Die zu konstruierende Strecke soll \(a\) sein aus \(a^2 = 15\,\text{cm}^2\). Jetzt können wir diese Fläche wieder mit einem Rechteck beschreiben, z.B. \(15\,\text{cm}^2 = 3\,\text{cm} \cdot 5\,\text{cm}\). Wir konstruieren dazu eine Grundseite \(c = 5\,\text{cm}\) und teilen sie in zwei Teile \(p = 3\,\text{cm}\) und \(q = 2\,\text{cm}\) auf.
Dann ziehen wir die Höhe hoch und schneiden sie mit dem Thaleskreis über der Hypotenuse. Wir erhalten das rechtwinklige Dreieck mit den beiden Katheten \(a\) und \(b\). Die Kathete \(a\) ist jetzt genau \(\sqrt{15}\,\text{cm}\) lang, da \(a^2 = 15\,\text{cm}^2\). Mit \(a\) haben wir somit die gesuchte Strecke konstruiert.
Aufgabensammlung
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.





Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.