Videos
Funktionsgraphen, die durch kontinuierliche Punktscharen \textit{ohne} Unterbruch beschrieben werden, heissen stetig.
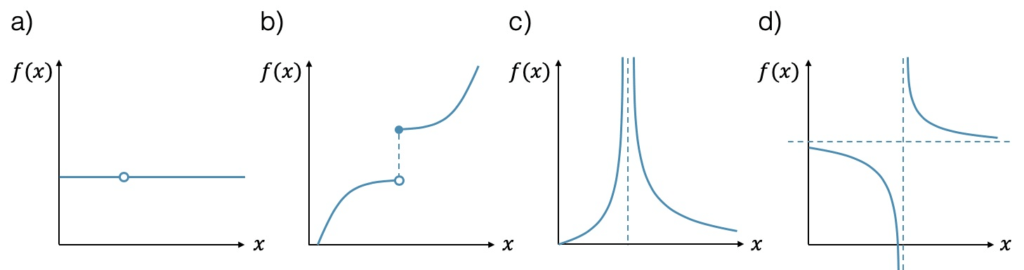
Die Stetigkeit kann an bestimmten Punkten, den sog. Unstetigkeitsstellen, unterbrochen sein:
- Löcher, d.h. Unterbrüche des Funktionsverlaufs
- Sprünge, d.h. der Funktionsverlauf springt auf eine neue Höhe
- Funktion verläuft ins Unendliche
- Funktion verläuft ins Unendliche, kombiniert mit einem unendlichen Sprung
Beispiel
Finde die Unstetigkeitsstellen der folgenden Funktion. Um welche Art von Unstetigkeitsstellen handelt es sich?
\[ f(x) = \frac{x^2-1}{x^2-2x-24} \]
Wir erhalten die Unstetigkeitsstelle, indem wir das Nennerpolynom null stellen:
\[ x^2-2x-24 \; \overset{!}{=} \; 0 \]
Links können mit mit dem Klammeransatz faktorisieren, denn der zweite Term ist \(4-6=-2\) und der dritte Term ist \(4 \cdot (-6) = -24\). Somit schreiben wir:
\[ (x+4)(x-6) = 0 \]
Wir sehen sofort, dass diese Gleichung erfüllt ist, wenn \(\underline{x=-4}\) oder \(\underline{x=6}\). Das sind unsere beiden Unstetigkeitsstellen.
Um die Art der Unstetigkeitsstellen herauszufinden, machen wir eine kleine Skizze des Graphen. Dazu ermitteln wir noch ein paar Punkte:
\[ f(0) = \frac{1}{24} \]
Das Zählerpolynom verrät uns die Nullstellen der Funktion:
\[ x^2 – 1 \; \overset{!}{=} \; 0 \]
\[ x^2 = 1 \]
Diese Gleichung hat zwei Lösungen: \(x=-1\) und \(x=1\).
Die Polynomdivision verrät uns zudem das Verhalten der Funktion im Unendlichen (Asymptote):
\[ (x^2-1) \;:\; (x^2-2x-24) \; = \; 1 + \text{Rest} \]
Damit schmiegt sich die Funktion der Asymptoten \(y=1\) an für \(x \rightarrow -\infty\) und \(x \rightarrow \infty\).
Der Verlauf der Funktion sieht in etwa folgendermassen aus:
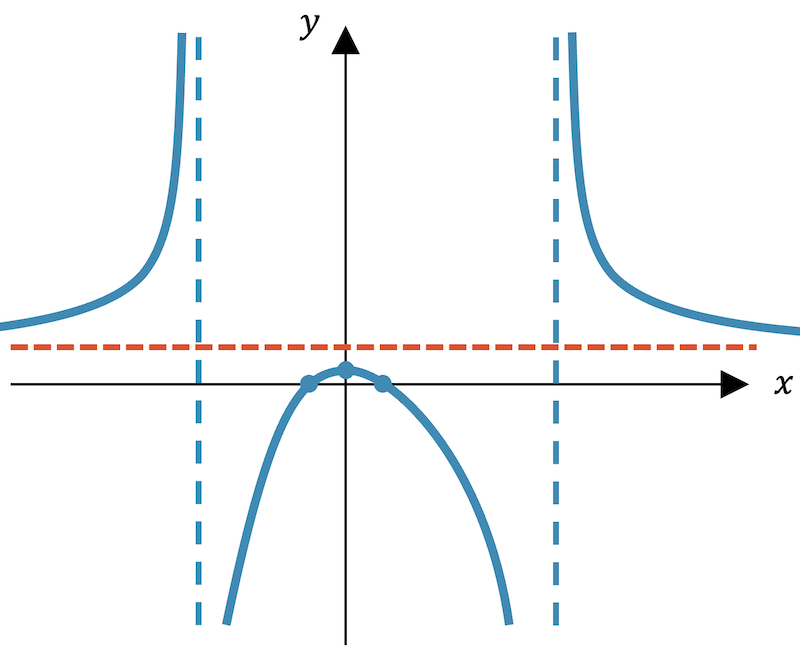
Die beiden Unstetigkeitsstellen sind unendliche Sprünge.
Beispiel
Untersuche die Stetigkeit der folgenden Funktion
\[ y(x)=\frac{x+1}{x-1} \]
Die Unstetigkeitsstelle finden wir, indem wir den Nenner auf null setzen. Der Nenner ist null für \(\underline{x=1}\).
Die Funktion hat eine Nullstelle in \(x=-1\), wie wir es im Zählerpolynom sofort erkennen können.
Den Achsabschnitt erhalten wir ebenfalls sehr schnell:
\[ f(0) = \frac{0+1}{0-1} = -1 \]
Schliesslich führen wir eine Polynomdivision durch und erhalten:
\[ (x+1) \;:\; (x-1) \;=\; 1 + \text{Rest} \]
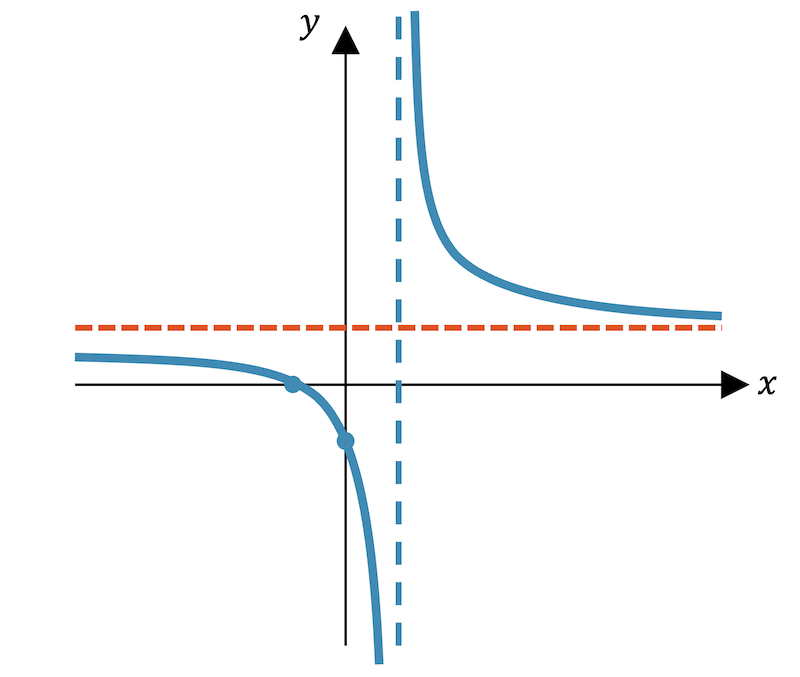
Damit ist die Asymptote wieder von der Form \(y=1\).
Der Verlauf zeigt uns, dass es sich um einen unendlichen Sprung handelt.
Aufgabensammlung
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.





Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.