Was macht die Collatz-Vermutung so faszinierend?

Die Collatz-Vermutung bzw. die (3x+1)-Vermutung ist bis heute eines der faszinierendsten Probleme der Mathematik. Lothar Collatz (1910 – 1990), deutscher Mathematiker, hat sich das wohl nicht so vorgestellt: Mit seiner Vermutung, die er 1937 aufstellte, löste er eine Faszination aus, die bis heute ungebrochen ist. Wir werden uns hier anschauen, was hinter der Vermutung steckt und warum sie so viel Leidenschaft in der Mathe-Welt auslösen konnte.

Eine sehr einfache Regel…

So geht sie: Du startest mit irgendeiner natürlichen Zahl. Ist sie gerade, teilst du sie durch zwei. Ist sie ungerade, multiplizierst du sie mit drei und addierst eine eins (3x+1). Alles klar?

Versuchen wir es mal mit der Zahl 13. Wir kriegen die folgende Zahlensequenz:

\[ 13 \rightarrow 40 \rightarrow 20 \rightarrow 10 \rightarrow 5 \rightarrow 16 \rightarrow 8 \rightarrow 4 \rightarrow 2 \rightarrow 1 \]

Nach 9 Schritten sind wir bei 1 angelangt. Beachte, dass die Sequenz hier nicht einfach stoppt. Denn 1 ist ja ungerade und hätte damit die Nachfolgezahl 4. Die hatten wir aber schon! Wir sind hier in einer unendlichen Schlaufe (Loop) gefangen, wo sich die Sequenz \(4 \rightarrow 2 \rightarrow 1 \) immer wiederholt.

Anderes Beispiel gefällig? Bestimme selber die Zahlenfolge mit Startwert 14. Du kannst deine Sequenz anschliessend vergleichen.

\[ 14 \rightarrow 7 \rightarrow 22 \rightarrow 11 \rightarrow 34 \rightarrow 17 \rightarrow 52 \rightarrow 26 \rightarrow 13 \]

\[ \rightarrow 40 \rightarrow 20 \rightarrow 10 \rightarrow 5 \rightarrow 16 \rightarrow 8 \rightarrow 4 \rightarrow 2 \rightarrow 1 \]

Dieses Mal waren 17 Schritte nötig, d.h. fast doppelt so viele! Du siehst auch, wie die Zahlen hoch und runtergehen. Sie werden deshalb auch Hagelzahlen genannt, in Analogie zu den kleinen Hagelkörnern, die in der Gewitterwolke hoch und runterfliegen, bis sie irgendwann als grosse Hagelkörner aus der Wolke herausfallen.

Die Mathematiker versuchten natürlich ein Muster hinter diesem Verhalten zu finden. Allerdings wurden sie überrascht. Die Folge mit Startzahl 26 führt in 10 Schritten zur 1 und steigt bis zur maximalen Zahl 40. Ihre Nachbarin, die Startzahl 27 hingegen, steigt bis auf 9’232 (!) und fällt erst nach 111 Schritten bis runter zur 1!

Bis heute konnte die Vermutung aber weder bewiesen, noch widerlegt werden. Interessanterweise sind andere Regeln recht überschaubar. Die (2x+1)-Regel etwa, führt immer ins Unendliche. Wenn wir eine ungerade Zahl haben und sie mit 2 multiplizieren, wird sie gerade. Wenn wir aber 1 hinzuaddieren, wird sie wieder ungerade. Das nimmt kein Ende und die Zahl wird immer grösser. Gerade Zahlen werden kleiner, indem sie halbiert werden. Sobald sie aber ungerade geworden sind, explodieren sie wieder ins Unendliche.

Eine Regel, die sich zufällig verhält?

Jemand fand heraus, dass die Anfangsziffern der Zahlen in der Sequenz einer gewissen Gesetzmässigkeit folgten. Hier müssen wir kurz etwas ausholen:

Im Jahr 1881 hatte der Astronom und Mathematiker Simon Newcomb (1835-1909) eine seltsame Entdeckung gemacht. Bis zur Erfindung des Taschenrechners mussten Logarithmenwerte in Büchern nachgeschaut werden. Er bemerkte, dass die Seiten mit der 1 als erste Ziffer viel schmutziger waren als die Seiten für andere Anfangsziffern. Newcomb ging dem nach und fand eine bestimmte Verteilung.

Unabhängig von ihm, veröffentlichte 1938 der Elektroingenieur und Physiker Frank Benford (1883–1948) die gleiche Gesetzmässigkeit, die er ebenfalls in Logarithmentafeln entdeckt hatte. Die Gesetzmässigkeit wird seither nach ihm benannt.

Das Benfordsche Gesetz gibt die typische Verteilung der Anfangsziffern von ”zufälligen” Zahlen. Weicht die Verteilung davon ab, handelt es sich um eine untypische Sammlung von Zufallszahlen. Heute wird dieses Gesetz etwa auf Umsatzzahlen von Unternehmen oder auf Wahlstimmen angewendet, um Unregelmässigkeiten aufzudecken.

Zurück zu unserer Collatz-Vermutung: Erstaunlicherweise gehorchen die Anfangsziffern der Zahlen aus den Collatz-Sequenzen dem Benfordschen Gesetz und ähneln somit wirklich einem natürlichen Zufall!

Wunderbare, korallenähnliche Strukturen

Vielleicht hattest du bis hierher auch schon die Idee, von der Endsequenz 4 \(^\rightarrow\) 2 \(^\rightarrow\) 1 rückwärts vorzugehen. Eine 1 kann nur aus dem Halbieren einer 2 entstehen. Eine 2 entsteht ebenfalls nur aus dem Halbieren einer 4. Die 4 kann aber aus der Schlaufe von der 1 herkommen oder sie entsteht aus dem Halbieren einer 8. Eine 8 kann nur aus einer 16 entstehen, denn 7 ist keine Dreierzahl. Die 16 entsteht aber aus einer 32 oder aus einer 5.

Wir zeichnen das ganze als einen gerichteten Graphen:

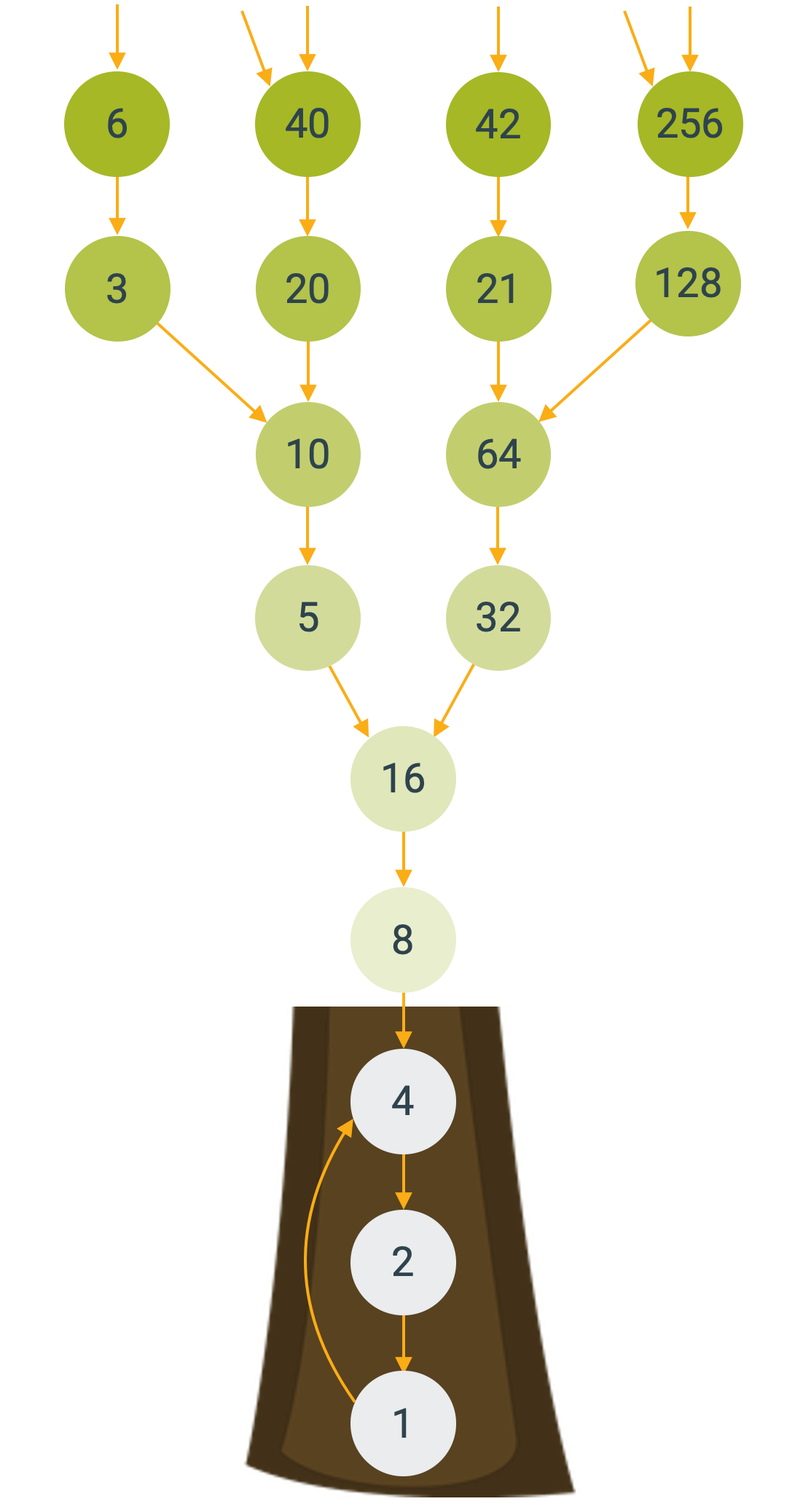
Die Collatz-Vermutung kann mit dem gerichteten Graphen visualisiert werden: Sie vermutet ja, dass sämtliche natürlichen Zahlen wie Blätter an einem Baum von dem einen und einzigen Stamm getragen werden, ohne dass es Äste gibt, die wieder nach oben zeigen oder in sich eine grosse Schlaufe bilden.

Eine andere Darstellung dieses Graphen ist die sog. Collatz-Koralle. Sie entsteht, wenn die Äste von oben nach unten in einem Winkel abgeknickt werden:

• um 20° im Gegenuhrzeigersinn, wenn der Ast zu einer ungeraden Zahl zeigt
• um 8° im Uhrzeigersinn, wenn der Ast zu einer geraden Zahl zeigt

Diese Visualisierung der Collatz-Vermutung ist auf erstaunlichste Art geformt. Sie erscheint ”zufällig” und wirkt ganz und gar natürlich. Hätten wir aufgrund einer klaren mathematischen Regel (3x+1) nicht irgendein Muster erwartet?

Vielleicht gibt es einen Gegenbeweis?

Das Beweisen ist manchmal sehr schwierig. Mit einem einzigen Gegenbeispiel wäre der Gegenbeweis bereits erbracht.

Bis heute ist jedoch niemandem weder Beweis, noch Gegenbeweis gelungen. Mit ”Brute Force”, d.h. durch einfaches Ausprobieren, hat man mit Computern alle natürlichen Zahlen bis \(2^68\) untersucht. Sie fielen alle irgendwann wieder ab zu 1. \(2^68\) ist tatsächlich eine riesige Zahl ist- Wir sehen das, sobald wir sie aufschreiben:

\[ 2^{68} = 295’147’905’179’352’825’856 \]

Kennst du die Legende vom Erfinder des Schachs und des Königs? Die Zahl \(2^{68}\) ist sogar grösser als die Anzahl Reiskörner, die der König hätte liefern sollen und ein x-faches der heutigen weltweiten Reisproduktion in einem ganzen Jahr! Soweit sieht es also gut aus für die Vermutung von Collatz.

Auch wenn \(2^{68}\) für unsere Vorstellungen ein grosse Zahl ist, ist sie das für die Mathematik nicht wirklich!

Der ungarische Mathematiker George Pólya (1887 – 1985), der lange Professor an der ETH Zürich war, stellte 1919 auch eine Vermutung auf. Seine Vermutung bestand ohne Beweis und Gegenbeweis bis ins Jahr 1958. Da geschah es aber: Ein Gegenbeweis wurde gefunden und das erst bei der Zahl \(1.845 \cdot 10^{361}\)! Das ist so viel mehr als \(2^{68}\)! Es ist deshalb alles noch offen und es könnte sein, dass viel weiter oben der Gegenbeweis doch noch aufwartet!

Der ebenfalls ungarische Mathematiker Paul Erdös soll gesagt haben:

Er meinte, dass wir aktuell nicht die geeigneten Mittel haben, ein solches Problem zu lösen. Mathe kann manchmal selbst für Mathematiker zu schwierig sein!

Füge unten einen kurzen Kommentar hinzu.