Hauptsatz der Integralrechnung

Herleitung

Wir nehmen das Integral von einer unbekannten unteren Grenze \(a\) bis zur oberen Grenze \(x\). Daraus definieren wir eine Funktion \(F\), die dem Argument \(x\) den Wert des Integrals zuordnet. Damit es kein Problem mit der fixen Grösse \(x\) gibt, verwenden wir für das Integral die Laufvariable \(s\):

\[ F(x) = \int_{a}^{x} f(s)\,ds \]

Jetzt leiten wir diese Funktion \(F(x)\) nach \(x\) ab:

\[ \frac{d}{dx} F(x) = \lim_{\Delta x \rightarrow 0}\Big(\frac{F(x + \Delta x) – F(x)}{\Delta x}\Big) \]

\[ = \lim_{\Delta x \rightarrow 0}\Big(\frac{\int_{0}^{x+\Delta x}f(s)\,ds – \int_{0}^{x}f(s)\,ds}{\Delta x}\Big) \]

\[ = \lim_{\Delta x \rightarrow 0}\Big(\frac{\int_{x}^{x+\Delta x}f(s)\,ds}{\Delta x}\Big) \]

Wir haben mit dem Trick \(F(b)-F(a) = \int_{a}^{b}f(s)\,ds\) aus der Differenz von zwei Integralen ein Integral gemacht. Dieses Integral beschreibt die Fläche von \(x\) bis \(x+\Delta x\) für die Funktion \(f(s)\).

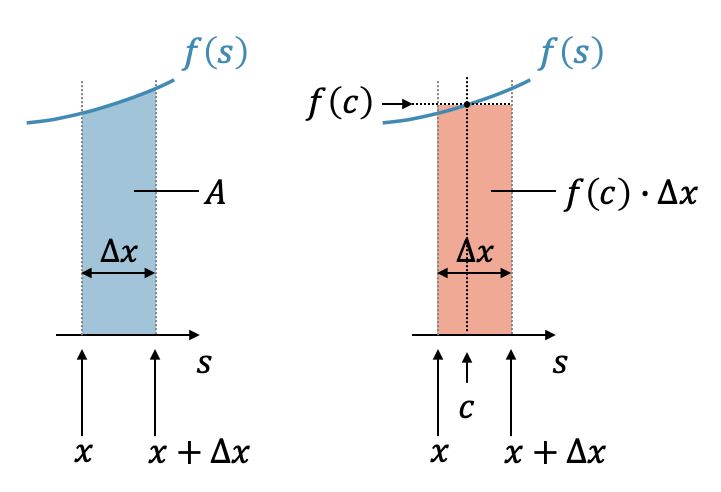
Nun benutzen wir den sog. Mittelwertssatz: Er besagt, dass die Fläche unterhalb von \(f(s)\) im betrachteten Intervall (blau) auch mit einem konstanten Mittelwert und somit als Rechteckfläche beschrieben werden kann (rot). Wie viel der Mittelwert ist und wo er genau von der Funktion erreicht wird, ist uns nicht bekannt. Wir wissen nur, dass es ihn gibt und sagen deshalb, dass er an der Stelle \(c\) ist, d.h. die Höhe \(f(c)\) mal die Breite \(\Delta x\) ergibt als Rechteckfläche die gleiche Fläche, wie das Integral:

\[ \int_{x}^{x+\Delta x} f(s)\,ds \quad = \quad f(c) \cdot \Delta x \]

Wir setzen das im Ausdruck oben ein und erhalten

\[ \frac{d}{dx} F(x) = \lim_{\Delta x \rightarrow 0}\Big(\frac{\int_{x}^{x+\Delta x}f(s)\,ds}{\Delta x}\Big) \]

\[ \require{cancel} = \lim_{\Delta x \rightarrow 0}\Big(\frac{f(c) \cdot \cancel{\Delta x}}{\cancel{\Delta x}}\Big) \]

\[ = \lim_{\Delta x \rightarrow 0}\big(f(c)\big) \]

Was passiert mit dem Wert \(f(c)\), wenn \(\Delta x \rightarrow 0\), d.h. immer kleiner wird? Die untere und die obere Grenze rücken näher zusammen und “quetschen” \(c\) gewissermassen ein. Am Schluss ist einfach \(x = c\). Somit schreiben wir: 

\[ \lim_{\Delta x \rightarrow 0}\big(f(c)\big) = f(x) \]

Wir setzen ein und erhalten:

\[ \frac{d}{dx} F(x) = \frac{d}{dx} \Big( \int f(x)\,dx \Big) = f(x) \]

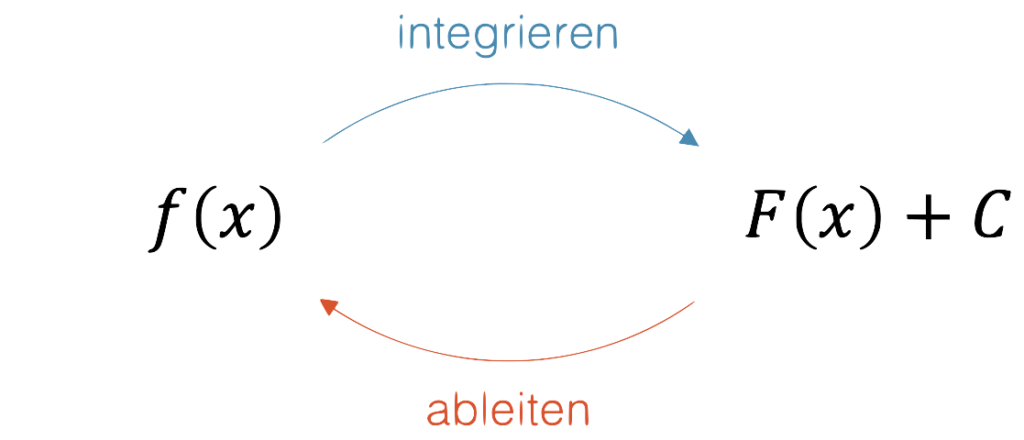
Das ist der Hauptsatz der Integralrechnung. Die Ableitung macht das Integrieren wieder rückgängig bzw. umgekehrt:

Wir haben in einem anderen Beispiel das Integral der Funktion \(f(x)=x\) ermittelt:

\[ f(s)=s \quad \rightarrow \quad \int_{0}^{x} f(s)\,ds = \frac{1}{2} x^2 \]

Damit haben wir die Stammfunktion \(F\) von \(f\):

\[ f(x) = x \quad \rightarrow \quad F(x) + C = \frac{1}{2} x^2 \]

Jetzt picken wir zwei Stammfunktionen aus der unendlichen Anzahl von möglichen Stammfunktionen für \(f(x)=x\) heraus:

\[ F_1(x)+C_1 = \frac{1}{2}x^2 \quad \text{mit} \quad C_1 = -1 \]

\[ \rightarrow \quad F_1(x) = \frac{1}{2}x^2 + 1 \]

\[ F_2(x)+C_2 = \frac{1}{2}x^2 \quad \text{mit} \quad C_2 = 0 \]

\[ \rightarrow \quad F_2(x) = \frac{1}{2}x^2 \]

Für beide gilt der Hauptsatz der Integralrechnung:

\[ \frac{d}{dx} F_1(x) = \frac{d}{dx} \Big( \frac{1}{2}x^2 + 1 \Big) = x = f(x) \]

\[ \frac{d}{dx} F_2(x) = \frac{d}{dx} \Big( \frac{1}{2}x^2 \Big) = x = f(x) \]

Die Funktionen \(F_1(x)\) und \(F_2(x)\) sind beide Stammfunktionen von \(f(x)\). Das \(C\) ist beliebig und deshalb unbekannt.

Bei der Ableitung der Stammfunktion fällt die Konstante \(C\) immer weg, denn deren Ableitung ist null. Deshalb fallen sämtliche Stammfunktionen (mit verschiedenen Konstanten \(C\)) alle auf die gleiche darunter liegende Funktion \(f(x)\).

Beispiel

Löse das folgende unbestimmte Integral:

\[ \int \Big ( x^2 + 2x -3 \Big )\,dx \]

---

Die Funktion, die es zu integrieren gibt ist:

\[ f(x) = x^2 + 2x -3 \]

Mit dem Integral wird jetzt die Stammfunktion \(F(x)\) gesucht, deren Ableitung gleich \(f(x)\) ist:

\[ \frac{d}{dx} F(x) = x^2 + 2x -3 \]

Wir kennen ja die Summenregel bei der Differentialrechnung. Sie gilt auch bei der Integration, d.h. wir können die einzelnen Summanden getrennt integrieren:

\[ \frac{d}{dx} \Big( \frac{1}{3}x^3 \Big ) = x^2 \]

\[ \frac{d}{dx} \Big( x^2 \Big ) = 2x \]

\[ \frac{d}{dx} \Big( -3x \Big ) = -3 \]

Daraus folgt:

\[ \frac{d}{dx} \Big ( \frac{1}{3}x^3 + x^2 – 3x\Big ) = x^2 + 2x -3 \]

Somit:

\[ \int \Big ( x^2 + 2x -3 \Big )\,dx = \frac{1}{3}x^3 + x^2 – 3x + C \]

Nicht vergessen: Bei einem unbestimmten Integral immer die unbekannte Konstante \(C\) noch hinzufügen.

Beispiel

Löse das folgende unbestimmte Integral:

\[ \int e^{-x}\,dx \]

---

Wir versuchen \(F(x)\) mit Raten zu finden. Wir leiten den geratenen Ausdruck nach \(x\) ab und schauen, ob wir als Resultat \(f(x) = e^{-x}\) erhalten:

\[ \frac{d}{dx}  \big( e^{-x} \big) = e^{-x} \cdot (-1) = -e^{-x} \quad \neq \quad f(x) \]

Wir ändern das Vorzeichen…

\[ \frac{d}{dx} \big( -e^{-x} \big) = -e^{-x} \cdot (-1) = e^{-x} \quad = \quad f(x) \]

Damit haben wir die Lösung gefunden:

\[ \int e^{-x}\,dx = -e^{-x} + C \]

‘Physiker-Trick’

Wir können den Hauptsatz der Integralrechnung auch mit einem einfachen Trick zeigen, der unter Physikern beliebt ist:

\[ \int f(x)\,dx = F(x) + C \]

Jetzt leiten wir die Gleichung beidseitig ab:

\[ \frac{d}{dx} \Big( \int f(x)\,dx \Big) = \frac{d}{dx} \Big( F(x) + C \Big) = \frac{d}{dx} F(x) + 0 \]

Wir konzentrieren uns vorerst auf die linke Seite der Gleichung. Das das Integral eine Summe ist, können wir die Summenregel für die Ableitung anwenden, d.h. die Ableitung einer Summe ist die Summe der Ableitungen der einzelnen Summanden:

\[ \frac{d}{dx}\big(a(x)+b(x)\big) = \frac{d}{dx}a(x) + \frac{d}{dx}b(x) \]

\[ \require{cancel} \frac{d}{dx} \Big( \int f(x)\,dx \Big) = \int \Big( \frac{d}{\cancel{dx}} f(x) \Big)\,\cancel{dx} = \int df \]

Das Integral ist die Summe aller kleinen “Stücke” \(df\), die zusammengesetzt natürlich wieder \(f(x)\) bilden müssen, d.h.

\[ \int df \; = \; f \]

Wir setzen das auf der linken Seite der Gleichung ein. Auf der rechten Seite hatten wir \(\frac{d}{dx} F(x)\). Wir erhalten so den Hauptsatz der Integralrechnung:

\[ f(x) =  \frac{d}{dx} F(x) \]