Videos
Es gibt Funktionen, für welche wir an gewissen Stellen die Steigung nicht bestimmen können, weil sie z.B. dort einen Sprung machen oder eine Lücke aufweisen. Das Erstellen der Ableitungsfunktion wird auch Ableiten oder mit dem Fremdwort Differenzieren genannt. Man nennt eine Funktion, deren Steigung an einer bestimmten Stelle nicht zu bestimmen ist, als nicht differenzierbar.
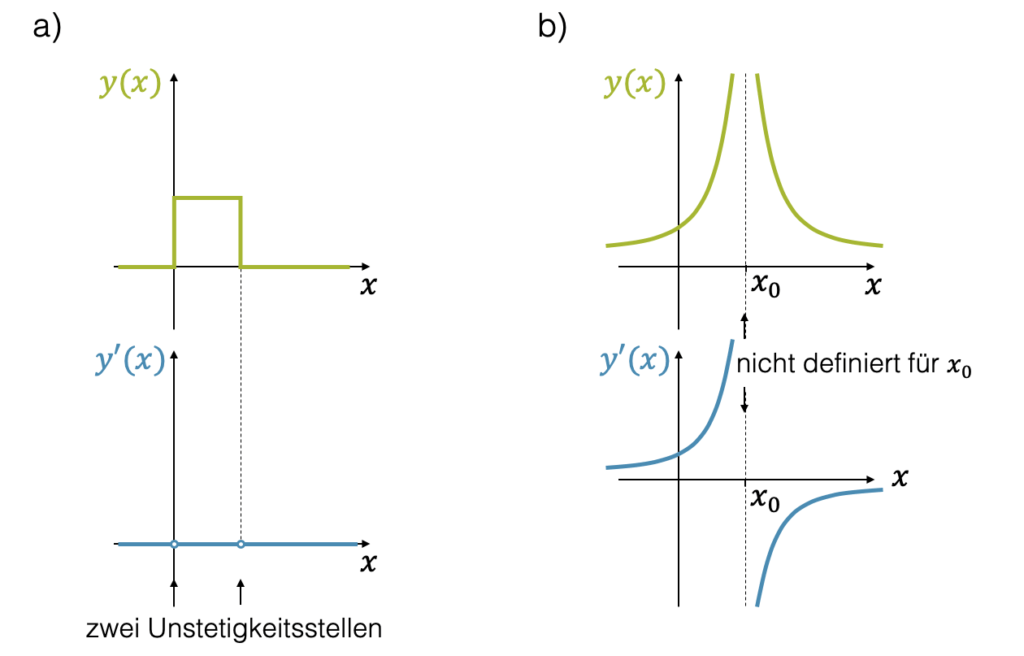
Die Funktion in a) (links) zeigt zwei Sprünge auf, die eigentlich einer unendlichen Steigung entsprechen. An diesen beiden Stellen ist die Funktion nicht differenzierbar. Die Ableitungsfunktion ist deshalb dort nicht definiert. Auf der rechten Seite hätte die Funktion an der Stelle \(x_0\) einen unendlichen Funktionswert, d.h. die Funktion ist an dieser Stelle unstetig. Wenn die Funktion an einer Stelle nicht definiert ist, kann natürlich ihre Steigung an der gleichen Stelle auch nicht angegeben werden.
Beachten Sie, dass eine Ableitungsfunktion durchaus Sprünge machen kann. Die Funktion zeigt an diesen Sprungstellen meistens “Knicke”, ist aber stetig.
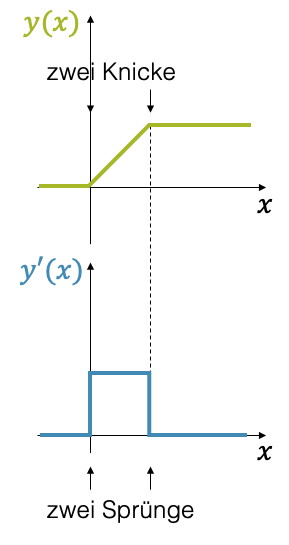
Aufgabensammlung
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.





Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.