Leistung

Definitionen

Abkürzung: \(P\) (engl. “power”, franz. “puissance”)

Einheit: \([P] = \mathrm{\frac{J}{s}} = \mathrm{W}\) (Watt)

Die Einheit Pferdestärken (\(\mathrm{PS}\)) ist noch sehr gebräuchlich, v.a. für die Leistung von Motoren. Sie wird in der Physik aber nicht mehr verwendet.

Achtung Verwechslungsgefahr!

• Die Arbeit \(W\) hat die Einheit \(\mathrm{J}\) (Joule)
• Die Leistung \(P\) hat die Einheit \(\mathrm{W}\) (Watt)

Grosse und kleine Leistung

Bei der Diskussion der physikalischen Arbeit und der Energien haben wir eine Grösse immer ignoriert: die Zeit!

Wir haben immer zwei Zustände vergleichen, vorher und nachher. Wie viel Zeit zwischen den beiden Zuständen war, haben wir nie berücksichtigt. Die Zeit spielt für den Unterschied zweier Energien keine Rolle!

Betrachten wir das folgende Beispiel: Beim Treppensteigen verrichten wir Hubarbeit. Für die Grösse der Arbeit spielt die Gewichtskraft \(F_g = mg \) und der Höhenunterschied \(\Delta h\) eine Rolle, nicht aber die Zeit:

\[ W \;\;=\;\; mg \cdot \Delta h \]

Wenn wir die Frau mit dem Kleinkind vergleichen, ist es offensichtlich, dass die Frau viel mehr leistet, als das Kleinkind.

• Die Frau hat eine grössere Gewichtskraft und macht den Höhenunterschied in kurzer Zeit
• Das Kleinkind ist viel leichter und nimmt sich mehr Zeit

Bei gleichem Höhenunterschied könnte die Frau auch langsam die Treppe hochsteigen. Auch in diesem Fall würde sie weniger leisten, als im Fall, wo sie die Treppe hochrennt.

Bei der Leistung \(P\) betrachten wir, wie viel Arbeit \(W\) pro Zeit \(\Delta t\) verrichtet wird. Mit der Energie heisst das: Wie stark die Energie sich ändert (\(\Delta E\)) pro Zeit \(\Delta t\).

\[ P = \frac{W}{\Delta t} = \frac{\Delta E}{\Delta t} \]

Die Leistung wird gross bei grossem Zähler oder kleinem Nenner:

• Grosser Zähler: Viel Arbeit \(W\), d.h. eine grosse Kraft oder ein grosser Höhenunterschied für die Hubarbeit
• Kleiner Zähler: Kleine Zeitspanne \(\Delta t\)

Welche Bedeutung hat die Leistung? Für unseren Körper bedeutet das kurzfristige Anstrengung, wie stark wir ins Schwitzen oder ins Keuchen kommen, wie schnell das Herz schlagen muss. In der Technik: Wie stark ein Motor sein muss.

Im folgenden Beispiel vergleichen wir einen Kleinwagen und einen grossen SUV. Vermutlich ist es nicht ganz falsch anzunehmen, dass beide Automodelle etwa gleich gut beschleunigen können.

Die Beschleunigungsarbeit ist definiert als:

\[ W \;\;=\;\; \frac{1}{2} m v_2^2 \;-\; \frac{1}{2} m v_1^2 \]

Wenn wir von der gleichen Startgeschwindigkeit, z.B. \(v_1 = 0 \) und der gleichen Endgeschwindigkeit z.B. \(v_2=50\;\text{km/h}\) ausgehen, dann gibt es nur noch einen Unterschied bei der Masse \(m\).

Der Kleinwagen hat eine vermutlich 2-3-fach kleinere Masse als der grosse SUV. Für die gleiche Beschleunigung braucht der SUV einen 2-3-mal stärkeren Motor, der 2-3-mal soviel Leistung bringen kann. Damit erreicht der SUV gerade mal die gleiche Beschleunigung, wie der Kleinwagen.

Schwere Autos haben deshalb immer einen grösseren und stärkeren Motor. Auch die Bremsen und Räder müssen für die grösseren Beschleunigungsarbeiten bereit sein.

Grosse Leistung: gleich viel Arbeit in kürzerer Zeit

Eine Masse wird angehoben. Dazu muss Hubarbeit geleistet werden. Wir nehmen an, dass es 60 J Arbeit sind.

Wenn wir für das Verrichten dieser Hubarbeit 20 Sekunden benötigen, dann errechnet sich die Leistung \(P\):

\[ P = \frac{W}{\Delta t} = \frac{60\,\mathrm{J}}{20\,\mathrm{s}} = 3\,\mathrm{W} \]

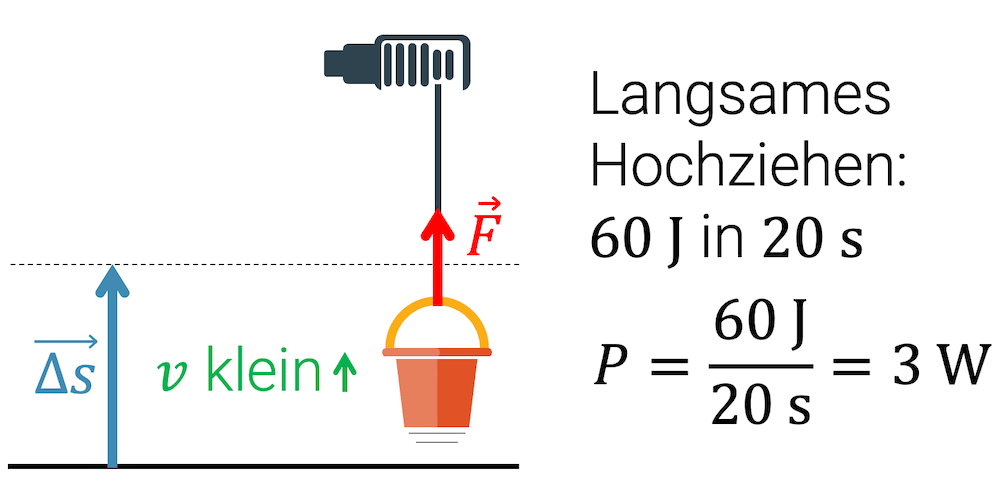
Für eine Leistung von 3 W reicht ein kleiner Motor, der diese Leistung erbringen kann.

Wenn wir aber die gleiche Arbeit in kürzerer Zeit verrichten möchten, dann ändert sich auf der Energie-/Arbeitsseite nichts. Die Masse ist immer noch gleich schwer, die Höhe ist immer noch gleich, d.h. es geht immer noch darum 60 J Hubarbeit zu leisten.

Was sich ändert, ist die Zeit \(\Delta t\): Wenn wir die gleiche Arbeit in nur 2 Sekunden erledigt haben möchten, erhalten wir:

\[ P = \frac{W}{\Delta t} = \frac{60\,\mathrm{J}}{2\,\mathrm{s}} = 30\,\mathrm{W} \]

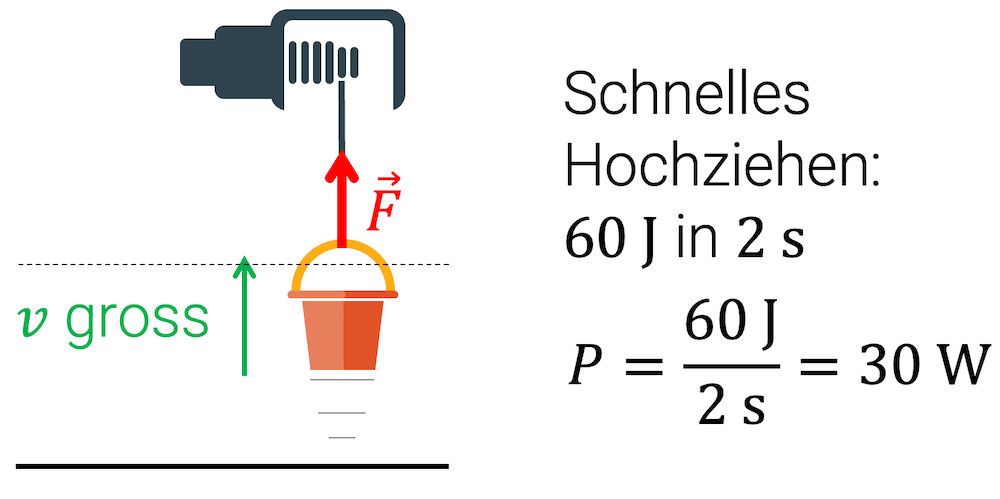
Es braucht einen grösseren Motor mit 10-facher Leistung! Dieser grössere Kranmotor kann die gleiche Last \(F\) über die gleiche Wegstrecke \(\Delta s\) anheben. Er macht es aber 10 mal schneller! 😎

Grosse Leistung: mehr Arbeit in gleiche Zeit

Aus der Definition der Leistung als Bruch von “Arbeit über Zeit”, erkennen wir, dass wir ein grosses \(P\) haben können, wenn der Zähler \(W\) (Arbeit) gross ist:

\[ P = \frac{W}{\Delta t} \]

In unserem vorigen Beispiel kann der grosse Kranmotor in der gleichen Zeit (20 Sekunden) die Masse 10-mal höher anheben oder er kann vielleicht sogar die 10-fache Masse anheben.

Umrechnung zwischen Leistung und Arbeit/Energie

Wir nehmen die Definition der Leistung und multiplizieren die Gleichung mit der Zeitperiode \(\Delta t\):

\[ \frac{W}{\Delta t} = P \]

\[ W = P \cdot \Delta t \]

So erhalten wir einen Ausdruck für die Berechnung der Arbeit. Auf die Frage hin “Wie viel Arbeit hat der kleine 3-Watt-Motor in 10 s geleistet?”, berechnen wir:

\[ W = 3\,\mathrm{W} \cdot 10\,\mathrm{s} = 30\,\mathrm{\frac{J}{s} \cdot s} = 30\,\mathrm{J} \]

Das ist natürlich die halbe Arbeit von vorhin, weil der Motor nur halb so lange gearbeitet hat.

Beachte, dass in der obigen Rechnung das erste \(W\) für die Arbeit (engl. “work”) und dann das zweite Mal \(\text{W}\) für die Einheit “Watt” steht.

Die Einheit Kilowattstunde ist eine Einheit für die Energie bzw. Arbeit. Sie entspricht analog zu \(W = P \cdot \Delta t\) der Multiplikation einer Leistung \(P\) mit einer Zeit \(\Delta t\):

\[ 1 \, \mathrm{kWh} = 1 \, \mathrm{kW} \cdot 1 \, \mathrm{h} \]

Eine Kilowattstunde ist der Arbeit, die bei einer Leistung von 1 kW über eine Stunde lang verrichtet worden ist.

Beispiel

Ein Kühlschrank nimmt im Schnitt 188 J in Form von elektrischer Arbeit in 10 Sekunden auf. Berechne seine Leistung in Watt, sowie die elektrische Arbeit, die der Kühlschrank in einem Jahr verbraucht, in Megajoule und in Kilowattstunden.

 

Lösung

Wenn der Kühlschrank 188 J pro 10 Sekunden braucht, dann sind es pro Sekunde 18.8 J an elektrischer Arbeit. Die Leistung beträgt demnach: \[ P = \frac{W}{\Delta t} \] \[ P = \frac{188\,\mathrm{J}}{10\,\mathrm{s}} = \frac{18.8\,\mathrm{J}}{1\,\mathrm{s}} = 18.8 \mathrm{\frac{J}{s}} = \underline{18.8\,\mathrm{W}} \] Anhand dieser Leistung können wir den Energiebedarf des Kühlschranks in einem ganzen Jahr berechnen: \[ \Delta E = P \cdot \Delta t = 18.8\,\mathrm{W} \cdot (365.25 \cdot 24 \cdot 3600)\,\mathrm{s} \] \[ \Delta E \approx 6 \cdot 10^8\,\mathrm{J} = \underline{600\,\mathrm{MJ}} \] Dabei haben wir benutzt, dass \(1\,\mathrm{MJ} = 10^6\,\mathrm{J}\). Üblicherweise werden solche Energieangaben in der Einheit Kilowattstunde angegeben: \[ W = \frac{600}{3.6} \, \mathrm{kWh} \approx \underline{167 \, \mathrm{kWh}} \]