Inhalt
Das Wichtigste in Kürze
Aus der idealen Gasgleichung folgt, dass die Isothermen im p-V-Diagramm Hyperbeln bilden. Für jeden Temperaturwert eine Hyperbel. Je höher die Temperatur, desto weiter oben (rechts) liegt die Hyperbel.
\[ p(V) = k \cdot \frac{1}{V} \]
Isothermen im p,V-Diagramm
Wenn wir eine Zustandsänderung eines Fluids bei konstanter Temperatur haben, dann bewegt sich der Punkt, der den Zustand im p-V-Diagramm beschreibt, auf einer Isothermen.
Die Isothermen sind Linien im p-V-Diagramm, die sämtliche Punkte verbindet, die dem gleichen Temperaturwert entsprechen. Eine Isotherme ist gewissermassen eine Höhenlinie der dreidimensionalen Fläche, die die Zustände \((p,V,T)\) beschreibt.
Im p-V-Diagramm schauen wir von “oben” auf diese “Landschaft”. Bewegt sich der Punkt auf einer Isothermen, so verändern sich die “Koordinaten” \((p,V)\), ohne dass sich die dritte “Koordinate” \(T\) ändert.
Für ideale Gase ist der Zusammenhang zwischen den Zustandsgrössen \(p\), \(V\) und \(T\) durch die ideale Gasgleichung gegeben. Bei konstanter Temperatur und konstanter Gasmenge haben wir eine Zustandsänderung nach dem Gesetz von Boyle-Mariotte.
\[ pV = nRT \quad \rightarrow \quad p(V)=(nRT)=\text{konstant} \]
\[ p(V) = k \cdot \frac{1}{V} \]
Wenn wir andere Buchstaben nehmen, erkennen wir sofort die sog. Hyperbelfunktionen:
\[ f(x) = k \cdot \frac{1}{x} \]
Für jeden Temperaturwert haben wir eine Hyperbel. Je höher die Temperatur, desto weiter oben (rechts) liegt die Hyperbel.
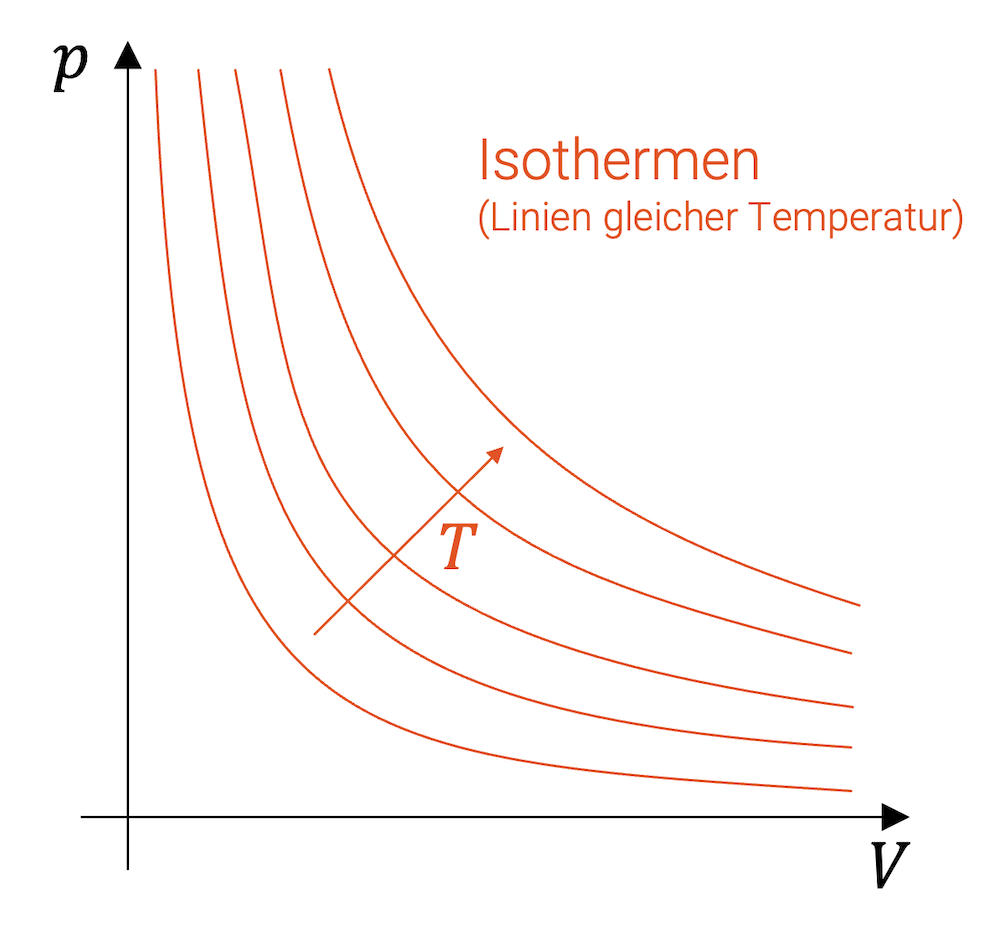
Eine isothermische Zustandsänderung bewegt sich auf der Isothermen der entsprechenden Temperatur.
Weitere Links
Isotherme Zustandsänderung (Wikipedia)
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt






Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.