Inhalt
Das Wichtigste in Kürze
Das Gesetz von Boyle-Mariotte besagt, dass eine konstante Menge eines Gases (\(n\) konstant) bei einer konstanten Temperatur \(T\) ein konstantes Produkt von Druck und Volumen hat:
\[ p_1 \cdot V_1 = p_2 \cdot V_2 \qquad (n, T \;\; \text{konstant}) \]
\[ p \cdot V = \text{konstant} \qquad (n, T \;\; \text{konstant}) \]
In der ersten Schreibweise bilden Druck und Volumen des Gaszustandes 1 das gleiche Produkt, wie Druck und Volumen des Gaszustandes 2.
Videos
Das Gesetz von Boyle-Mariotte das wohl bekannteste und einfachste Gasgesetz. Es ist benannt nach den Wissenschaftlern R. Boyle (1627-1691) und E. Mariotte (1620-1684), die beide das gleiche Gesetz, unabhängig von einander aufgestellt haben.
Beide schauten sich eingeschlossene Gase an und analysierten das Zusammenspiel von Druck und Volumen. Sie fanden ein Gesetz für den Spezialfall, wo die Temperatur und die Stoffmenge konstant gehalten werden (eingeschlossenes Gas).
Das Gesetz von Boyle-Mariotte besagt, dass eine konstante Menge eines Gases (\(n\) konstant) bei einer konstanten Temperatur \(T\) ein konstantes Produkt von Druck und Volumen hat:
\[ p_1 \cdot V_1 = p_2 \cdot V_2 \qquad (n, T \;\; \text{konstant}) \]
\[ p \cdot V = \text{konstant} \qquad (n, T \;\; \text{konstant}) \]
In der ersten Schreibweise bilden Druck und Volumen des Gaszustandes 1 das gleiche Produkt, wie Druck und Volumen des Gaszustandes 2.
Beispiele
Das Gesetz von Boyle-Mariotte können wir an zahlreichen Beispielen erkennen:
- Beim Einatmen vergrössern wir das Volumen unserer Lunge und der Druck sinkt unmittelbar. Es fliesst dann aber sofort Luft nach, um den Druck wieder auszugleichen.
- Beim Trinken mit einem Trinkhalm vergrössern wir das Volumen in der Mundhöhle mit unserer Zunge und der Druck sinkt. Als Folge drückt der Luftdruck auf die Oberfläche des Getränks und stösst damit das Getränk den Halm hinauf in die Mundhöhle, um den Druck wieder auszugleichen.
- Durch das Verkleinern des Volumens in einer Velopumpe erhöhen wir den Druck um den gleichen Faktor.
- Wegen des leicht geringeren Drucks in der Flugzeugkabine blasen sich Chipstüten oder Joghurtbecher innerlich auf, d.h. die eingeschlossene Luft nimmt mehr Volumen ein.
- Wetterballone starten von der Erdoberfläche mit einem kleinen Volumen. In hoher Atmosphäre nehmen sie durch den kleineren Umgebungsdruck ein grösseres Volumen ein.
- Taucher lernen als Erstes in der Tauchschule, dass sie beim Aufsteigen ausatmen müssen. Der Grund: Beim Aufsteigen nimmt der Umgebungsdruck stark ab und die Luft in der Lunge würde volumenmässig so stark zunehmen, dass die Lunge lebensgefährlich verletzt würde.
Beispiel
Auf welches Volumen müssen wir einen Liter Luft komprimieren, um den Druck von \(1\;\text{bar}\) auf \(4\;\text{bar}\) zu erhöhen?
Beispiel
Um welchen Faktor vergrössert sich eine Luftblase, wenn sie von \(50\;\text{m}\) Tiefe an die Oberfläche aufsteigt, wenn der Umgebungsluftdruck rund \(1\;\text{bar}\) beträgt?
Herleitung aus der idealen Gasgleichung
Das Gesetz von Boyle-Mariotte kann, wie auch alle anderen Gasgesetze, einfach aus der idealen Gasgleichung hergeleitet werden. Dazu nehmen wir die universelle Gasgleichung
\[ pV = nRT \]
Jetzt überlegen wir uns welche Grössen beim Prozess konstant bleiben werden. Beim Gesetz von Boyle-Mariotte sind das die Stoffmenge \(n\) und die Temperatur \(T\).
Der Druck \(p\) und das Volumen \(V\) verändern sich.
Wir müssten jetzt an dieser Stelle mit Hilfe von Algebra alle variablen Grössen auf die linke Seite der Gleichung bringen und alle konstanten Grössen auf die rechte Seite der Gleichung. Bei Boyle-Mariotte ist es besonders einfach, denn die sind alle schon am richtigen Ort: Die variablen Grössen \(p\) und \(V\) stehen schon links und rechts haben wir ausschliesslich konstante Grössen, nämlich \(n\), \(T\) und \(R\), die ja eine Konstante ist. Die Gleichung steht also unverändert:
\[ pV = (nRT) \]
Jetzt besteht die Klammer rechts nur aus konstanten Grössen, d.h. die ganze rechte Seite ist konstant. Wir können deshalb auch schreiben: \(p \cdot V = \text{konstant}\) oder
\[ p_1 V_1 = p_2 V_2 \]
womit wir das Gesetz von Boyle-Mariotte erhalten haben.
Wir können es aber auch mit Hilfe des Teilchenmodells herleiten.
Was ist Druck? Druck ist die Kraft, mit welcher ein Gas auf eine Fläche \(A\) wirkt. Diese Kraft sind die vielen Kraftstösse der Teilchen über die Zeit gemittelt.
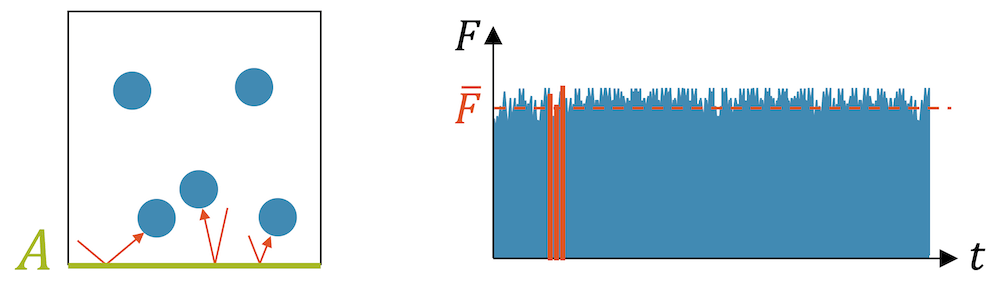
Diese Stösse sind elastische Stösse, die wir als Kraftstösse im Rahmen des Impulses diskutiert haben: Ein Teilchen ändert durch den Stoss seinen Impuls, was einer Krafteinwirkung entspricht.
Kraft pro Fläche ist bekanntlich Druck. Wir haben deshalb im Gasbehälter einen Gasdruck \(p\):
\[ p = \frac{F}{A} \]
Wenn wir den quaderförmigen Behälter vergrössern, indem wir die Seitenlängen verdoppeln, wird das Volumen dadurch 8 mal grösser. Das Gas ist jetzt im Behälter quasi 8-fach “verdünnt”.
Teilchen, die auf direktem Weg auf die Fläche \(A\) zufliegen, werden jetzt eine doppelte Strecke zurücklegen müssen. Das braucht doppelt so viel Zeit. Die Fläche \(A\) wird deshalb nur noch halb so oft Stösse erfahren, obwohl es die gleichen Teilchen sind und sie sich immer noch gleich schnell bewegen. Die Kollisionen werden seltener und die über die Zeit gemittelte Kraft halbiert sich:
\[ F \quad \rightarrow \quad \frac{F}{2} \]
Die Seiten der quadratischen Fläche \(A\) wurden durch die Vergrösserung verdoppelt, so dass die Fläche 4-fach vergrössert wurde:
\[ A \quad \rightarrow \quad 4A \]
Wir setzen diese Veränderungen in unsere Druckgleichung ein und erhalten einen Druck, der 8-fach kleiner wird:
\[ p = \frac{F}{A} \quad \rightarrow \quad \frac{\Big(\frac{F}{2}\Big)}{\big(4A\big)} = \frac{1}{8} \frac{F}{A} \]
Zusammengefasst heisst das: Wenn wir das Volumen \(V\) 8-fach vergrössern, wird der Druck \(p\) 8-fach kleiner. Damit haben wir das Gesetz von Boyle-Mariotte wieder: Das Volumen vergrössert sich um den gleichen Faktor, wie der Druck sich verkleinert.
Konstruktion der Isothermen im Druck-Volumen-Diagramm (p-V-Diagramm)
Das Gesetz von Boyle und Mariotte gilt für Zustandsänderungen mit konstanter Temperatur (und konstanter Stoffmenge).
Zustandsänderungen, in welchen die Temperatur konstant bleibt (wie im Fall von Boyle-Mariotte) zeichnen sich dadurch aus, dass sie sich auf einer sog. Isothermen bewegen, einer Linie, die für eine bestimmte Temperatur gilt.
Wir nehmen das Gesetz von Boyle-Mariotte…
\[ p \cdot V = \text{konstant} \]
…und schreiben für die Konstante einfach \(k\). Dann dividieren wir durch \(V\):
\[ p \cdot V = k \quad \rightarrow \quad p(V) = k \cdot \frac{1}{V} \]
Wenn wir dies in ein \(p,V\)-Diagramm eintragen, ergibt das eine Hyperbel (analog zu \(f(x) = \frac{1}{x}\)) mit der \(p\)-Achse und der \(V\)-Achse als Asymptoten.
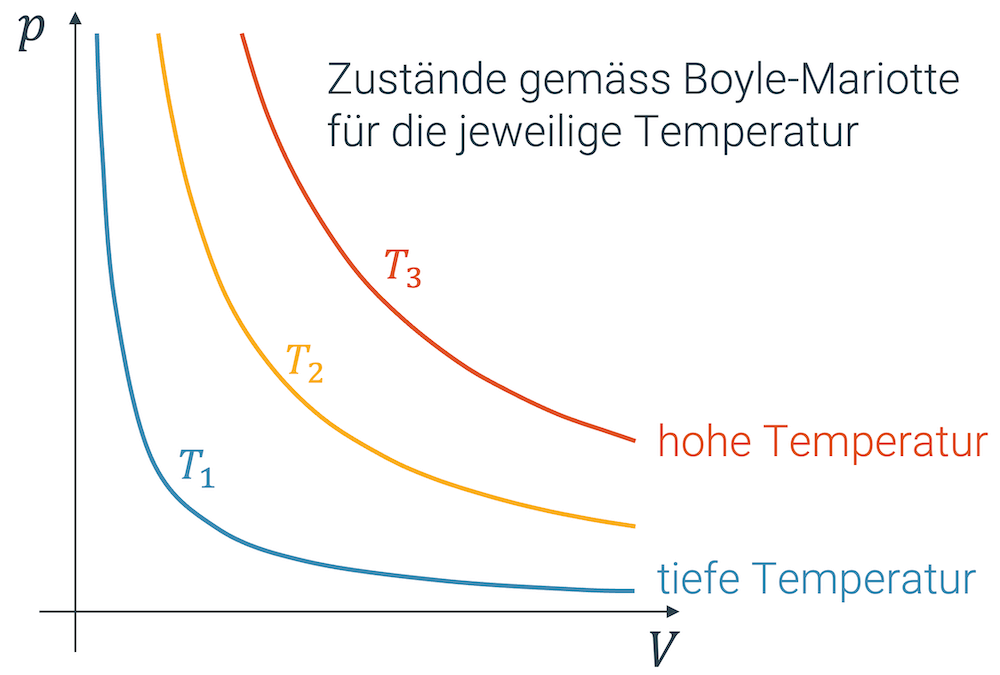
Nehmen wir z.B. die unterste blaue Kurve im obigen Diagramm, so sehen wir sehr schön, wie der Druck bei kleiner werdendem Volumen zunimmt oder umgekehrt, wie der Druck abnimmt, wenn wir das Gas expandieren.
Jede Hyperbel steht für eine bestimmte, konstant gehaltene Temperatur.
Die Kurve wird deshalb auch Isotherme genannt. “Iso” steht für “gleich” und “therme” für “thermischen Zustand”, der durch die Temperatur beschrieben wird.
Alle Punkte auf der Hyperbel entsprechen Zuständen bei der gleichen Temperatur, die durch die Anwendung von Boyle-Mariotte erreicht werden können.
Wie wir auf die anderen Hyperbeln kommen, die für höhere Temperaturen stehen, schauen wir uns jetzt an: Wir nehmen ein Volumen und erwärmen dieses. Die Teilchen bewegen sich schneller, sie prasseln mit mehr Geschwindigkeit und somit mit mehr Impuls auf die Behälterwände, was zu einer grösseren mittleren Kraft und somit zu einem grösseren Druck führt.
Bei gleichem Volumen, haben wir jetzt durch die höhere Temperatur einen höheren Druck erhalten, d.h. wir haben jetzt eine grössere Konstante \(k\).
Jetzt lassen wir die Temperatur aber wieder konstant und wenden das Gesetz von Boyle-Mariotte mit dem grösseren \(k\) an. Es gibt uns eine weitere Hyperbel, die aber auf einem höheren Druckniveau liegt.
Aufgabensammlung
Weitere Links
Thermische Zustandsgleichung idealer Gase (Wikipedia)
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt









Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.