Inhalt
Das Wichtigste in Kürze
Der Schwerpunkt eines Körpers ist ein theoretischer Punkt, in welchen wir uns die gesamte Masse des Körpers denken können. Der Rest des Körpers wird zur masselosen Hülle. Dieses Modell ist sehr praktisch, da wir z.B. die Bewegung eines Massepunktes mit Hilfe der Newton’schen Gesetze sehr einfach beschreiben und berechnen können. Der Körper wird sich genau so bewegen. Er wird möglicherweise um seinen Schwerpunkt herum drehen.
Der Schwerpunkt eines Körpers kann in einfachen Fällen berechnet, bei geometrischen Figuren konstruiert und für unförmige Körper experimentell bestimmt werden. Wir können aber auch einen gemeinsamen Schwerpunkt für mehrere Körper bestimmen. Beispielsweise bilden die Erde und der Mond ein “Körperpaar”, das sich um den gemeinsamen Schwerpunkt herumdreht.
Videos
Häufigste Fragen

Beispiele
Der Schwerpunkt befindet sich meist “etwa in der Mitte” eines Körpers. Da es sich um einen theoretischen Punkt handelt, kann er sich auch dort befinden, wo es gar keine Materie hat.
Ein einfacher Ring hat zum Beispiel seine Masse regelmässig rundherum verteilt. Der Schwerpunkt des Rings befindet sich offensichtlich in der geometrischen Mitte, wo es aber keine Masse hat.
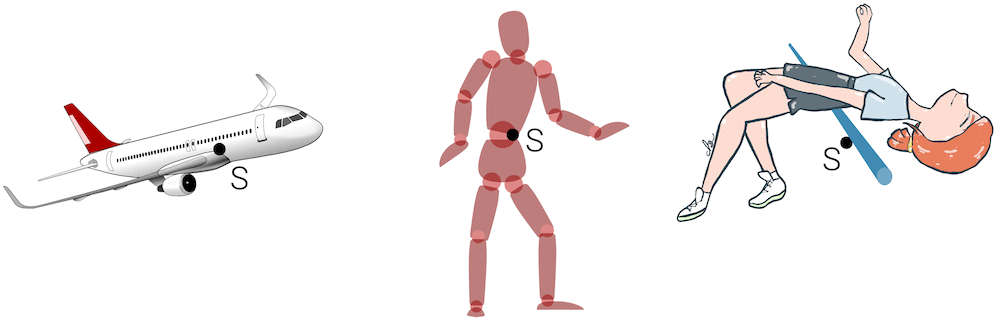
Wir können den Schwerpunkt unseres Körpers, der sich meist in der Bauchgegend befindet, aus dem Körper herausbringen. Im Hochsprung wird beim Fosbury-Flop genau das erreicht und zwar mit einem praktischen Nutzen: Der Schwerpunkt befindet sich auf geringerer Höhe als der gekrümmte Körper.
Da der Schwerpunkt der Stellvertreter für die ganze Masse ist, bedeutet das im Prinzip “Die ganze Masse muss nicht über die Latte springen”. Dank des Fosbury-Flops kann jeder Mensch mit gleicher Kraft höher springen, weil der Schwerpunkt nicht so hoch gebracht werden muss.
Grafische Bestimmung des Schwerpunkts
Für geometrische Formen reicht es, den Schnittpunkt von zwei Symmetrieachsen zu nehmen und schon hat man den Schwerpunkt.
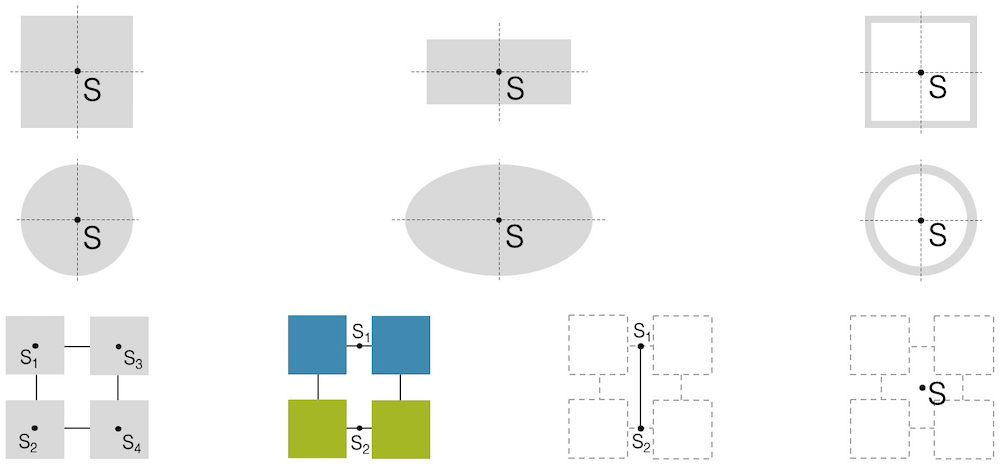
Der Schwerpunkt von zusammengesetzten Formen kann ebenfalls mit einem einfachen Trick ermittelt werden, der in der untersten Reihe angedeutet ist: Man wählt zwei Teilkörper, die die gleiche Masse haben und deren Schwerpunkt bekannt ist. In diesem Beispiel je zwei Quadrate mit dem Schwerpunkt in der jeweiligen Mitte.
Der Schwerpunkt der zusammengesetzten Figur von zwei Quadraten liegt in der Mitte zwischen den beiden Schwerpunkten. Wir kriegen so die Schwerpunkte S1 für die beiden blauen und S2 für die beiden grünen Quadrate.
Der Schwerpunkt für blau und grün kombiniert, ist der Punkt S in der Mitte auf der Verbindung zwischen S1 und S2. Dieser liegt, wie wir aus Symmetriegründen schon wussten, in der Mitte der Quadrate.
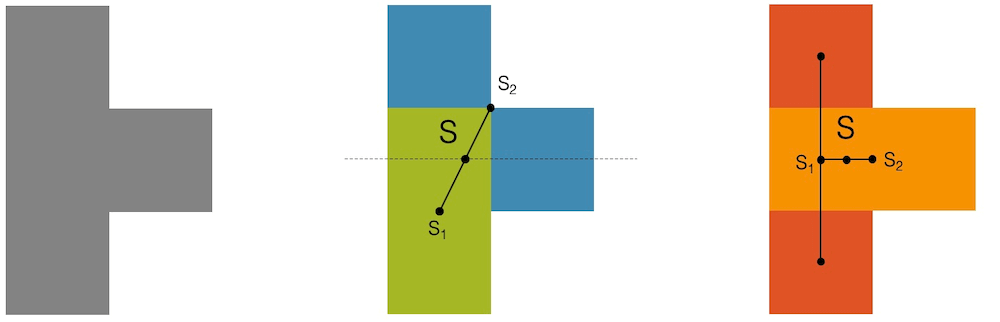
Im nächsten Beispiel ist es klar, dass der Schwerpunkt auf der mittleren Höhe sein muss, da das eine Symmetrieachse ist. Doch wo genau liegt er? Wir sehen hier zwei Möglichkeiten:
- In der Mitte wird eine blaue und eine grüne Figur miteinander kombiniert. Die Schwerpunkte S1 und S2 der blauen und grünen Figuren verbinden wir und finden in der Mitte, da beide Figuren die gleiche Masse haben, den Schwerpunkt S.
- Rechts sind die zwei andere Figuren in rot und orange markiert. Verbinden wir die beiden Schwerpunkte S1 (rot) und S2 (orange) und schneiden wir die Verbindung in der Hälfte durch, erhalten wir wieder den gleichen Schwerpunkt S.
Bestimmung durch Ausbalancieren
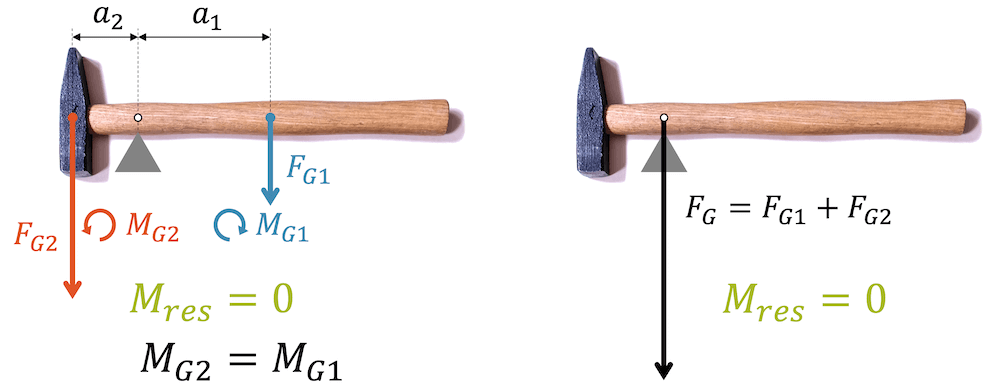
Für unförmige Körper oder Körper bestehend aus unterschiedlich dichten Materialien, können wir den Schwerpunkt nicht konstruieren. Wir können ihn aber experimentell durch Ausbalancieren leicht bestimmen:
Dazu legen wir den Hammer auf einen Auflagepunkt (z.B. unseren Finger) und suchen den Punkt in welchem der Hammer ausbalanciert ist.
In diesem Fall sind nämlich alle Drehmomente links und rechts gleich gross und heben sich auf. Wir können die Drehmomente links zusammenfassen mit einem Drehmoment \(M_{G2}\) und die Drehmomente rechts mit \(M_{G1}\).
Beide sind gleich gross, haben aber die umgekehrte Richtung. Es herrscht Drehmomentgleichgewicht (\(M_{res} = 0\)): Der Hammer ist in Ruhe und verbleibt in Ruhe, d.h. er wird nicht beschleunigt.
Das Gleiche haben wir, wenn die gesamte Masse im Schwerpunkt gedacht wird und der Hammer darum herum nur eine leere Hülle ist. In diesem Fall greift nur eine Gewichtskraft an.
Weil sie durch den Auflagepunkt geht, verursacht sie kein Drehmoment, das Drehmomentgleichgewicht gilt und der Hammer kippt nicht weg.
Bestimmung mit der Aufhängemethode
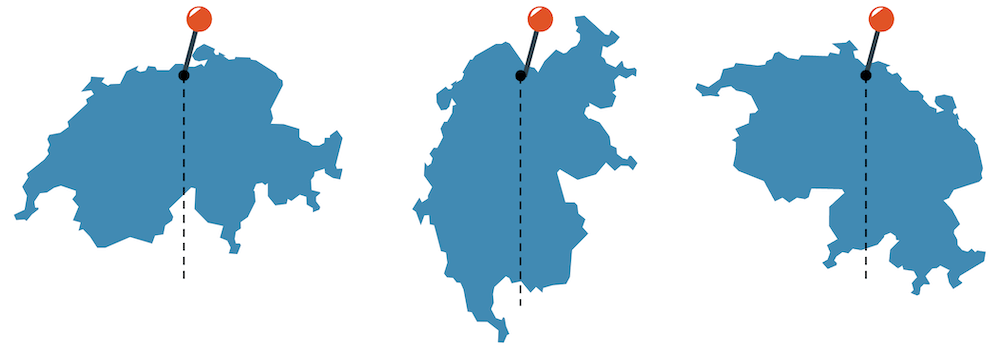
Wir können auch den Körper an einem beliebigen Punkt aufhängen und das Lot aufzeichnen. Dann hängen wir den Körper an einem anderen beliebigen Punkt auf und zeichnen das zweite Lot. Alle Linien schneiden sich im Schwerpunkt, d.h. mit zwei Linien haben wir den Schwerpunkt schon gefunden (die dritte Linie ist eigentlich überflüssig).
Der Mittelpunkt der Schweiz liegt übrigens auf einer hübschen kleinen Alp im Melchtal, im Kanton Obwalden.
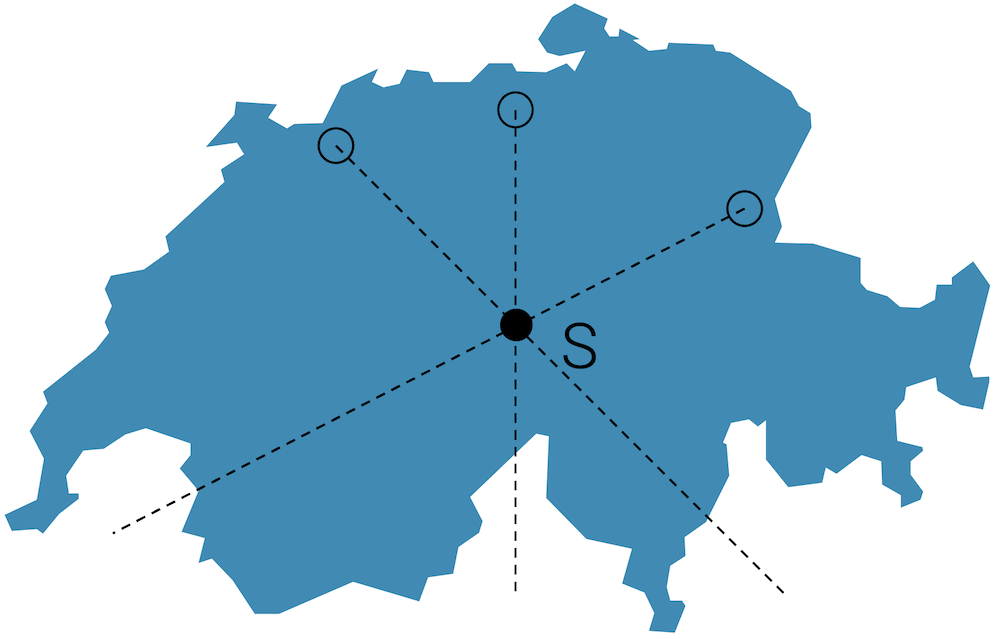
Warum ist das so? Durch das Aufhängen balanciert der Körper sich aus und wählt einen Winkel, in welchem er links und rechts Drehmomentgleichgewicht erreicht.
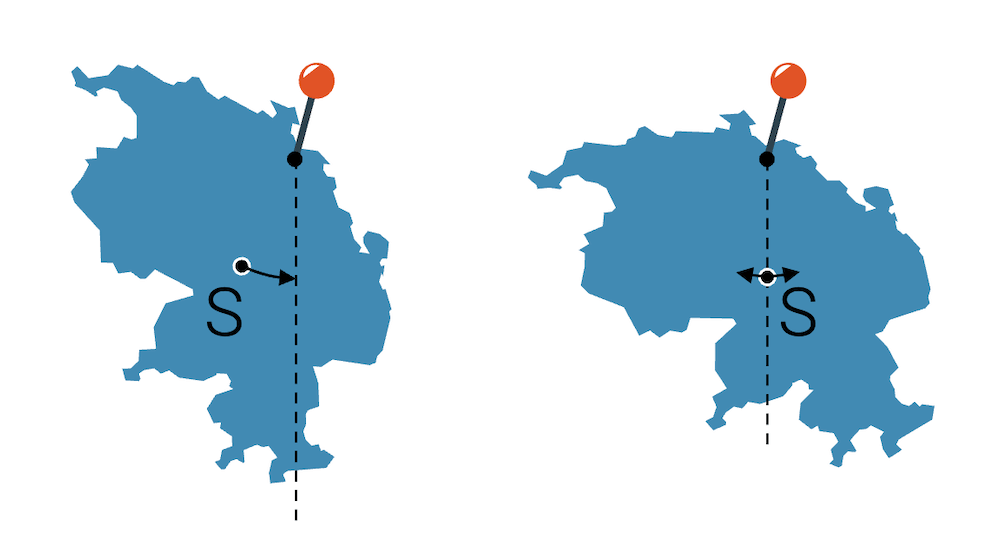
Wir können uns die gesamte Masse des Körpers im Schwerpunkt konzentriert und den Körper als leere Hülle vorstellen.
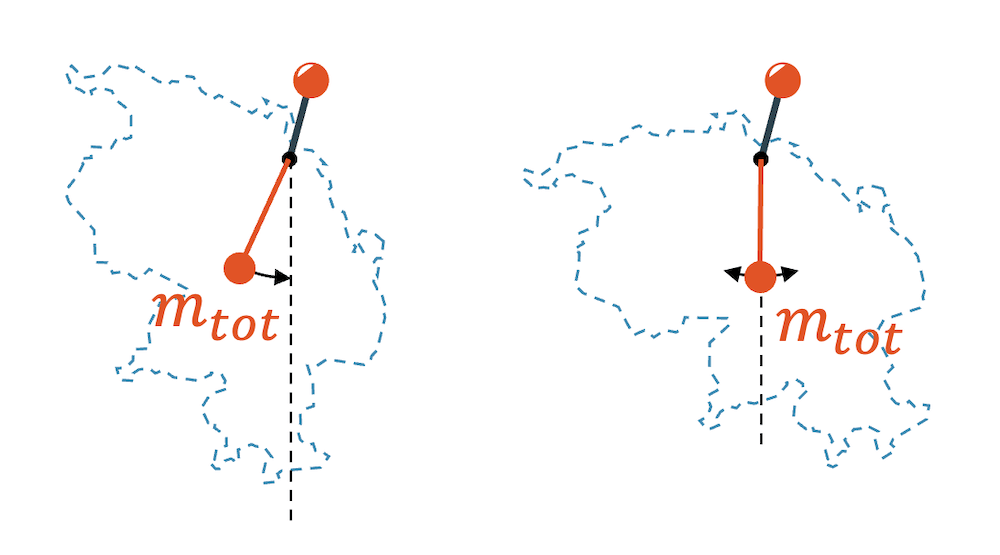
Die gesamte Masse \(m_{tot}\) hängt wie ein Pendel an einem Faden und wird sich entsprechend einpendeln, bis die Masse im tiefsten Punkt, genau unterhalb des Aufhängepunkts, zu liegen kommt.
Berechnung des Schwerpunkts
Der Schwerpunkt ist der Stellvertreter für die ganze Masse eines Körpers, d.h. wir können uns einen Körper als masselose Hülle vorstellen, die ihre ganze Masse im Schwerpunkt vereint hat. Dieser neue theoretische Körper soll sich aber genau gleich verhalten und anfühlen wie der normale Körper.
Wo die Masse verteilt ist, ist für das Drehmoment von Bedeutung. Wir müssen deshalb den Schwerpunkt so platzieren, dass das Drehmoment der Gewichtskraft gleich ist, wie alle Drehmomente von allen Massen im Körper zusammengezählt.
Am vereinfachten Beispiel des Hammers wollen wir das anschauen.
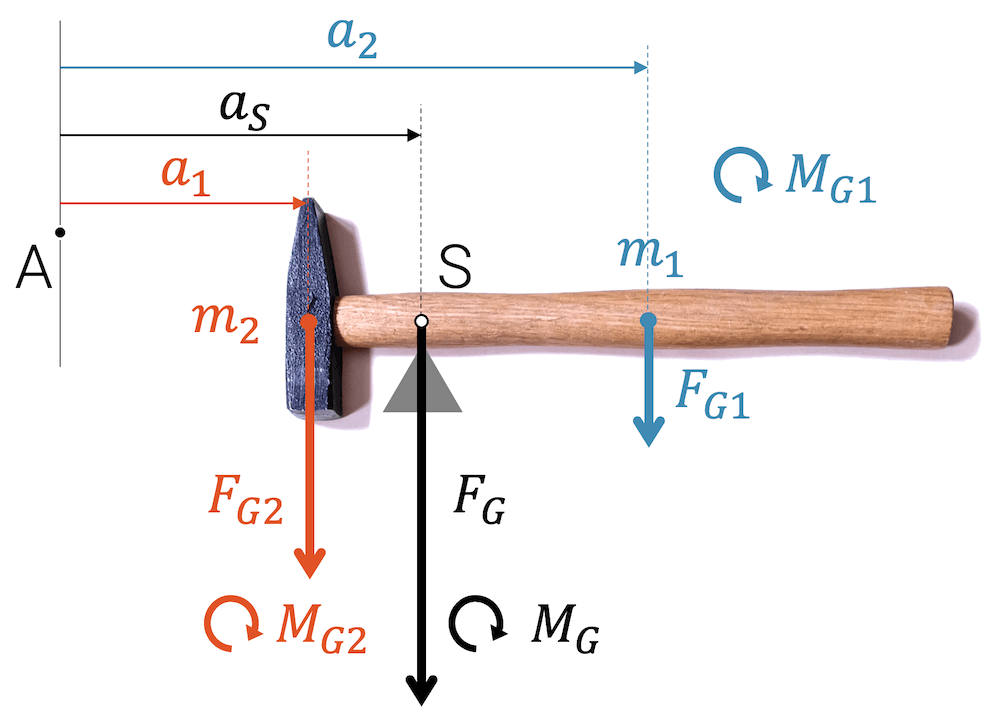
Der Holzkörper hat seinen Schwerpunkt in seiner geometrischen Mitte. Er vereint die Masse des ganzen Holzes \(m_1\). Der Metallkörper hat auch seinen eigenen Schwerpunkt in seiner Mitte, mit der Masse \(m_2\). Wie können wir jetzt den Schwerpunkt S für den ganzen Hammer bestimmen?
Wir wählen einen Punkt A und bestimmen die beiden bekannten Drehmomente \(M_1 = F_1 \cdot a_1\) und \(M_2 = F_2 \cdot a_2\). Nun fordern wir, dass ein Drehmoment gleich der Summe dieser beiden Drehmomente ist:
\[ M_G = M_1 + M_2 \]
Gleichzeitig soll dieses Drehmoment von der Gewichtskraft im Schwerpunkt herkommen. Wir wissen nicht, wo der Schwerpunkt ist, nehmen aber einfach an, wir wüssten es und nennen diesen unbekannten Abstand \(a_S\):
\[ M_G = F_G \cdot a_S \]
Nun setzen wir diesen Ausdruck oben ein und erhalten:
\[ F_G \cdot a_S = F_1 \cdot a_1 + F_2 \cdot a_2 \]
Für die Gewichtskräfte setzen wir \(F_G = mg\), \(F_1 = m_1 g\) und \(F_2 = m_2 g\) ein und kürzen die Erdbeschleunigung \(g\) überall weg:
\[ m \cdot a_S = m_1 \cdot a_1 + m_2 \cdot a_2 \]
Jetzt dividieren wir durch die Masse \(m\) und erhalten den Ausdruck für den Ort des Schwerpunkts:
\[ a_S = \frac{m_1}{m} \cdot a_1 + \frac{m_2}{m} \cdot a_2 \]
Für den Abstand des Schwerpunkts nimmt man offenbar einfach die einzelnen Abstände \(a_i\) der “Teil-Schwerpunkte” und gewichtet sie mit der Teilmasse \(m_i\).
“Ein freier Körper rotiert um seinen Schwerpunkt herum”
Rotation um den Schwerpunkt
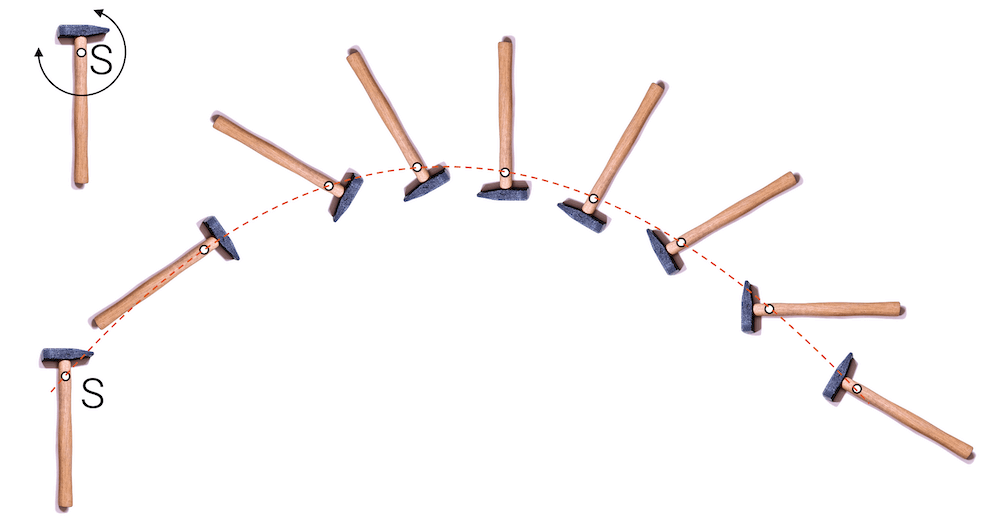
Ein freier Körper rotiert um seinen Schwerpunkt herum. In der Bildfolge oben sehen wir, wie der Schwerpunkt eines fliegender Hammers eine parabolische Flugbahn einnimmt, während der Körper des Hammers um den Schwerpunkt herum rotiert.
Warum ist das so? Stell dir vor, du klebst einen Kaugummi auf den kleinen Rotor eines Handventilators. Wenn der Kaugummi nicht wegfliegt, dann eiert und vibriert der Propeller jetzt ziemlich stark.
Das sind die Zentripetalkräfte, die auf den Kaugummi wirken und ihn in die Kreisbewegung um die Rotationsachse zwingen. Diese Kräfte wirken auch auf das Propellermaterial, aber dort sind sie ausbalanciert und heben sich gegenseitig auf, so dass der Propeller ohne Kaugummi sehr ruhig läuft.
Würde der Propeller (mit Kaugummi) alleine durch die Luft fliegen und rotieren, gäbe es nichts, was ihn an die alte Rotationsachse erinnern würde. Er würde einfach um seinen neuen Schwerpunkt herum rotieren und die Kräfte wäre ausbalanciert.
“Selbst nach der Explosion haben die Bombenfragmente immer noch den gleichen gemeinsamen Schwerpunkt!”
Schwerpunkt als Massenzentrum eines Systems

Wir betrachten eine Sprengstoffkugel (Masse \(m\)) vor der Explosion. Der Schwerpunkt liegt in der Mitte der Kugel und ist in Ruhe (links).
Jetzt zünden wir den Sprengstoff und stoppen den “Film” unmittelbar nach der Explosion (rechts). Wir haben keine Kugel mehr, aber einen Körper, der aus vielen Fragmenten besteht, die in alle Richtungen fliegen.
Die Summe der Fragmente muss, weil die Masse erhalten bleibt, immer noch \(m\) betragen.
Die Masse ist aber nicht mehr gleich verteilt. Dennoch ist ihr Schwerpunkt immer noch der Gleiche. Es ist sogar so, dass der Schwerpunkt auch nach der Explosion immer noch in Ruhe ist!
Dafür verantwortlich ist wieder Newtons Erster Satz der besagt, dass ein Körper, dessen resultierende Kraft null ist, nicht beschleunigt wird.
Ist er in Ruhe vor der Explosion, so ist er es auch nach der Explosion. Er explodiert ja von innen heraus und nicht durch eine äussere Krafteinwirkung.
Die Betrachtung eines Massezentrums ist in der Teilchenphysik sehr üblich, v.a. bei der Diskussion von Teilchenkollisionen. Schauen wir uns aber ein Beispiel aus der Astrophysik an:
Der Mond dreht sich um die Erde? Eigentlich bilden Erde und Mond ein Paar, das sich um ihren gemeinsamen Schwerpunkt drehen, wie das Metallstück und der Holzgriff beim fliegenden Hammer.
Das Erde-Mond-System kreist um die Sonne, nicht die Erde alleine, d.h. der Schwerpunkt der beiden läuft um die Sonne (siehe gestrichelte, schwarze Linie). Die Erde “schwabbelt” um diese Linie herum.
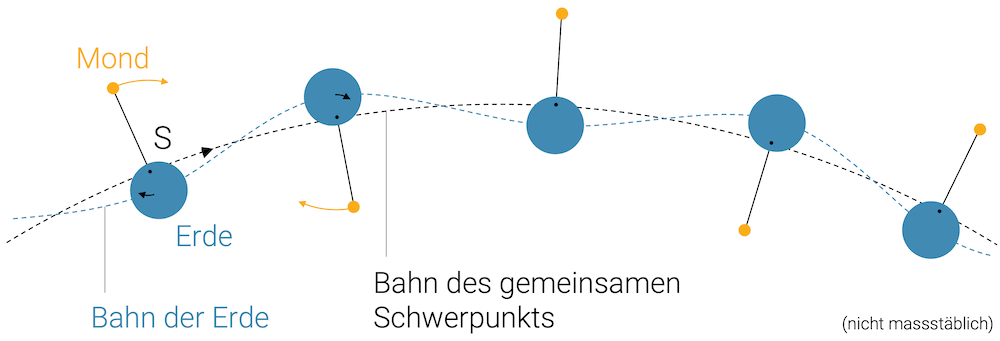
Auch interessant ist die Tatsache, dass der Mond rund 384’000 km von der Erde entfernt ist. Der gemeinsame Schwerpunkt liegt aber noch in der Erde drin.
Die Erde hat im Vergleich zum Mond eine rund 81-fache Masse, d.h. wir müssten 81-mal näher am Schwerpunkt der Erde sein, als am Schwerpunkt des Monds. Somit teilen wir den Abstand Erde – Mond in (81+1) Teile:
\[ 384’000\;\text{km} : 82 = 4’683\;\text{km} \]
Da der Erdradius etwa 6’371 km beträgt, liegt der gemeinsame Schwerpunkt rund 1’700 km unter der Erdoberfläche auf der dem Mond zugewandten Seite.
Berechnung mit einem Integral
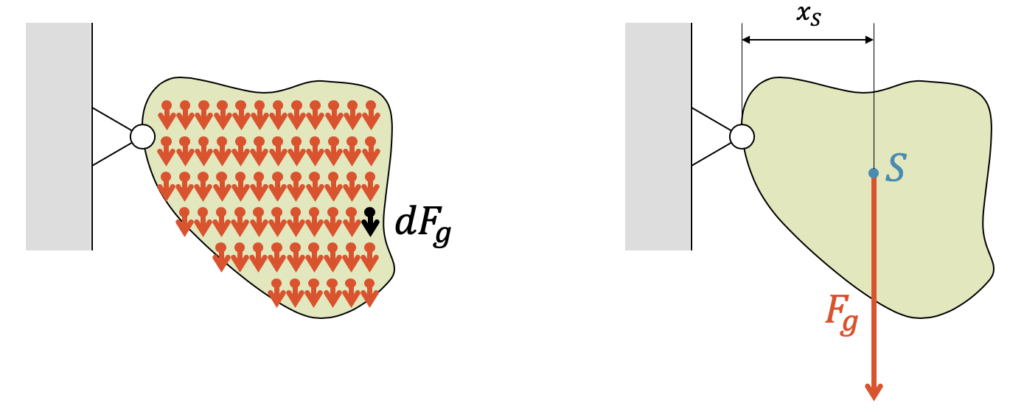
Wir erinnern uns nochmals an die Definition des Schwerpunkts: Er vereint die gesamte Masse und ist so platziert, dass er von überall gesehen das gleiche Drehmoment erzeugt, wie die im Körper verteilte Masse. Eine kleine Teilmasse erzeugt eine kleine Teil-Gewichtskraft \(dF_g\). Für den ganzen Körper müssen die Teil-Gewichtskräfte integriert werden und wir erhalten die Gewichtskraft:
\[ F_g = \int dF_g \]
Je weiter diese Teil-Gewichtskraft vom betrachteten Drehpunkt entfernt ist (Abstand \(x\)), desto grösser ist das Teil-Drehmoment \(dM\). Für das Gesamt-Drehmoment aller Teil-Gewichtskräfte, müssen wir die Teil-Drehmomente integrieren. Dieses Integral muss dann aber das gleiche Drehmoment erzeugen, wir die gesamte Gewichtskraft \(F_g\) im Schwerpunkt, der im Abstand \(x_S\) liegt:
\[ dM = x \cdot dF_g \]
\[ M = \int dM = \int x \cdot dF_g \]
\[ \stackrel{!}= \quad x_S \cdot F_g \]
Jetzt lösen wir die Gleichung nach dem gesuchten Abstand \(x_S\) des Schwerpunkts auf, indem wir durch die Gewichtskraft \(F_g\) dividieren und sie dann mit dem Integral von oben ersetzen:
\[ x_S = \frac{\int x \cdot dF_g}{F_g} = \frac{\int x \cdot dF_g}{\int dF_g} \]
Das ist im Wesentlichen schon die Lösung. Durch die Berechnung dieses Bruchs mit den beiden Integralen haben wir die Position des Schwerpunkts berechnet. Eigentlich ist es nur die Schwerelinie, die Vertikale, die durch den Schwerpunkt verläuft. Der Abstand \(x_S\) beschreibt die Position der Schwerelinie, sagt uns aber nicht auf welcher Höhe der Schwerpunkt liegt.
Um das herauszufinden, braucht es eine zweite Schwerelinie, denn zwei Linien kreuzen sich in einem Punkt, oder wir benutzen die Symmetrie, z.B. wissen wir dass der Schwerpunkt auf der Mittellinie eines symmetrischen Objekts liegen muss.
Beispiel
Zeige, dass der Schwerpunkt des Rechtecks der Länge \(L\) bei \(x_S = \frac{L}{2}\) ist.
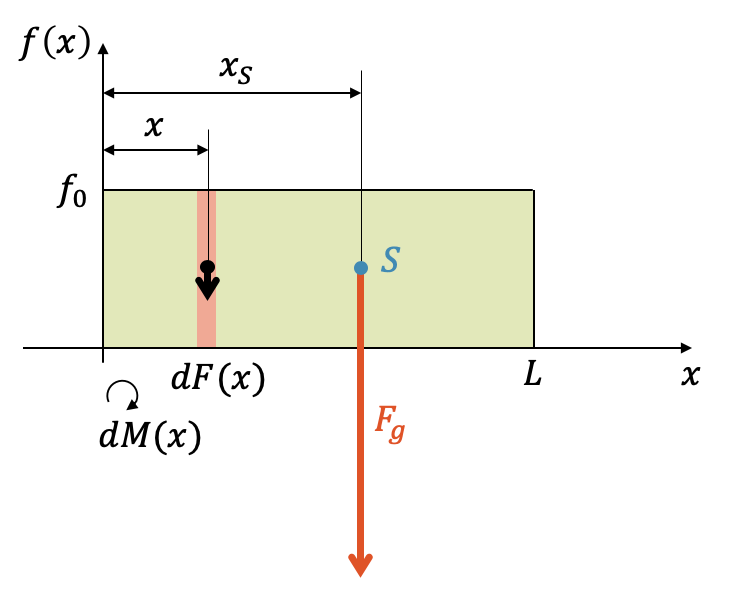
Im Abstand \(x\) haben wir die infinitesimale Gewichtskraft \(dF(x)\). Diese Gewichtskraft ist abhängig von der Funktion \(f(x)\). Je grösser \(f(x)\), desto mehr Gewicht wird an dieser Stelle \(x\) sein und desto grösser ist die Teil-Gewichtskraft \(dF(x)\). Wir schreiben deshalb einfach \(dF(x)=f(x) \cdot dx\), d.h. \(f(x)\) für die Höhe und \(dx\) für die Breite. Wir nehmen an, dass die Dichte des Materials schon in \(f(x)\) berücksichtigt ist.
Im einfachen Fall eines Rechtecks ist \(f(x)\) ein konstanter Wert und zwar einfach \(f_0\) für alle \(x\). Somit:
\[ dF(x) = f(x) dx = f_0 dx \]
Jetzt können wir den Abstand zum Schwerpunkt berechnen:
\[ x_S = \frac{\int_0^L x \cdot dF(x)}{\int_0^L dF(x)} \]
\[ = \frac{\int_0^L x \cdot f_0\;dx}{\int_0^L f_0\;dx} = \frac{f_0 \int_0^L x\;dx}{f_0 \int_0^L\;dx} \]
\[ \require{cancel} = \frac{\cancel{f_0} \cdot \frac{1}{2} \big[x^2\big]_0^L}{\cancel{f_0} \cdot \big[x\big]_0^L} = \frac{\frac{1}{2} (L^2-0^2)}{L-0} \]
\[ = \underline{\frac{L}{2}} \]
Der Abstand \(x_S\) zur Schwerelinie, in welcher sich der Schwerpunkt befindet, kann wie folgt berechnet werden:
\[ x_S = \frac{\int x \cdot f(x) \; dx}{\int f(x) \; dx} \]
Dabei beschreibt \(f(x)\) die Verteilung der Masse als Funktion des Abstands \(x\).
Beispiel
Finde den Abstand zur Schwerelinie \(x_S\) im rechtwinkligen Dreieck mit der Kathetenlänge \(s\).
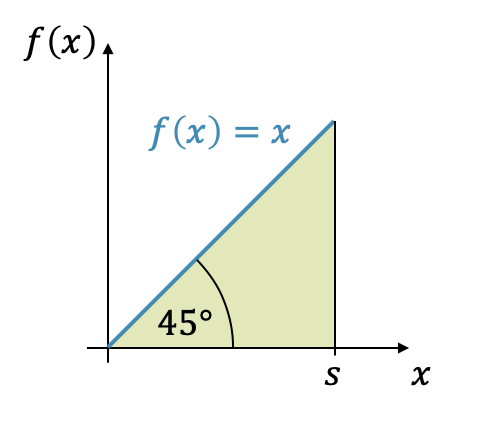
Der Körper kann mit der Funktion \(f(x)=x\) beschrieben werden. Für die Berechnung des Abstands \(x_S\) zur Schwerelinie benutzen wir ein Integral von \(0\) bis \(L\):
\[ x_S = \frac{\int_0^s x \cdot f(x) \; dx}{\int_0^s f(x) \; dx} \]
\[ = \frac{\int_0^s x \cdot x \; dx}{\int_0^s x \; dx} = \frac{\big[\frac{1}{3}x^3\big]_0^s}{\big[\frac{1}{2}x^2\big]_0^s} \]
\[ x_S = \frac{\frac{1}{3}(s^3-0^3)}{\frac{1}{2}(s^2-0^2)} \]
\[ = \underline{\frac{2}{3}s} \]
Der Schwerpunkt liegt zwei Drittel einer Kathetenlänge \(s\) entfernt. Aus Symmetriegründen teilt die andere Schwerelinie das Dreieck ebenfalls auf der Höhe von zwei Dritteln einer Kathete (von oben gerechnet).
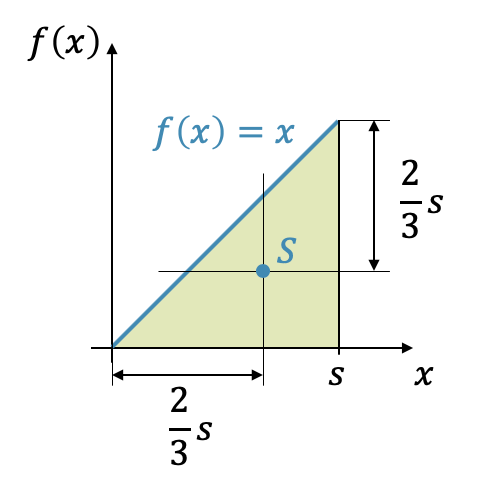
Aufgabensammlung
Lernziele
- Du verstehst, welche Rolle der Schwerpunkt spielt, für einen oder mehrere Körper zusammen.
- Du weisst, dass ein freier Körper oder ein freies System aus mehreren Körpern um den gemeinsamen Schwerpunkt rotieren.
- Du kannst den Schwerpunkt grafisch bestimmen, v.a. auch mit der Methode des Kreuzpunkts zweier Verbindungslinien.
- Du kannst den Schwerpunkt mathematisch bestimmen und ihn mit dem Drehmomentgleichgewicht in Bezug bringen.
Weitere Links
Massenmittelpunkt (Wikipedia)
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt









Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.