Linsen

Linsen sind transparente Objekte mit gekrümmten Oberflächen, so dass interessante optische Eigenschaften entstehen. Die Umlenkung der Lichtstrahlen entsteht aufgrund der Brechung an den Grenzflächen der Linse. Linsen sind deshalb besonders interessant, weil sie scharfe reelle und virtuelle Bilder erzeugen können.

Unser Auge erzeugt mit Hilfe einer Linse ein reelles scharfes Bild auf der Netzhaut. Dort wo die Augenlinse 👀 an ihre Grenzen kommt, helfen uns zusätzliche Linsen (Brillen, Kontaktlinsen etc.), um trotzdem ein scharfes Bild zu sehen.

Optische Instrumente wie das Mikroskop 🔬 oder das Teleskop 🔭, aber auch die einfache Lupe 🔍 funktionieren dank Linsen und erzeugen vergrösserte Bilder, die wir sonst nie sehen könnten.

Linsen werden auch in Scheinwerfern und Strahlern eingesetzt, indem sie z.B. die Lichtstrahlen geeignet bündeln.

Grundsätzlich gibt es auch Linsen für andere Wellenarten. Deren Funktionsweise entspricht weitgehend derjenigen der optischen Linsen für sichtbares Licht.

Linsenformen

Grundsätzlich wird zwischen Sammellinsen und Streulinsen unterschieden:

• Sammellinsen (oft auch Konvexlinsen genannt) sind in der Mitte dicker als aussen, d.h. sie sind “bauchig”
• Streulinsen (oft auch Zerstreuungslinsen oder Konkavlinsen genannt) sind in der Mitte dünner als aussen und sie zerstreuen parallele Strahlen von der optischen Achse weg

Schliesslich gibt es noch die Fresnel-Linsen, die den Effekt der Sammel- oder Streulinsen erreichen, jedoch mit Hilfe von Abstufungen, so dass sie ziemlich flach realisiert werden können.

Sammellinsen (Konvexlinsen)

Die Sammellinsen vereinen (fokussieren) die parallelen Lichtstrahlen hinter der Linse im sog. Brennpunkt. Der Abstand des Brennpunkts von der Linsenebene heisst Brennweite \(f\).

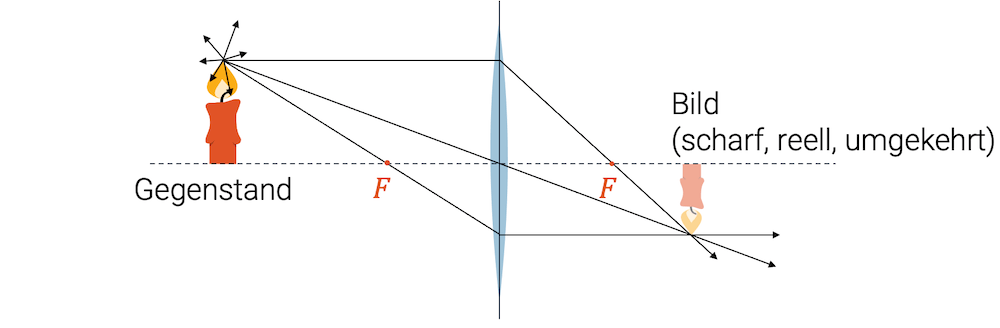
Sammellinsen sind die interessantere Gruppe, weil sie unterschiedliche Arten von Bildern erzeugen können:

• vergrösserte oder verkleinerte oder umgekehrte, reelle Bilder
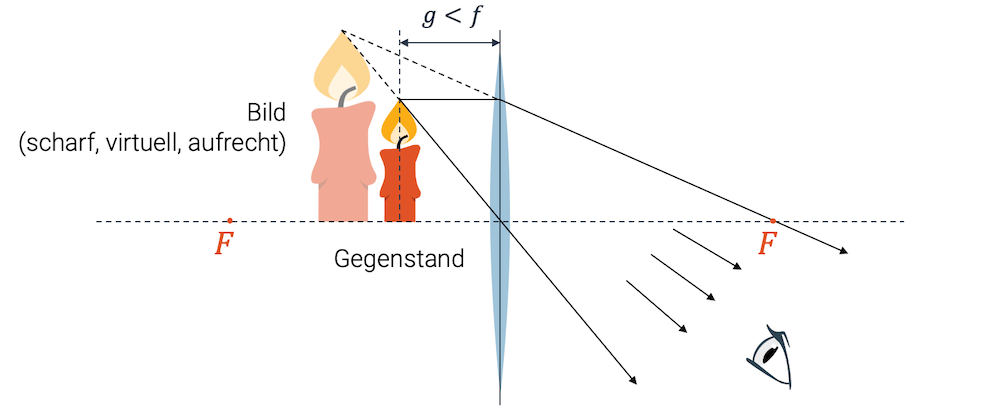
• aufrechte vergrösserte virtuelle Bilder

Die physikalisch interessante Eigenschaft teilen die Sammellinsen mit den Konkavspiegeln (Hohlspiegel).

Sammellinsen haben viele Anwendungen:

• Die Augenlinse ist eine Sammellinse
• Brillen oder Kontaktlinsen für Weitsichtige sind Sammellinsen
• Lupen
• Mikroskope und Teleskope bestehen aus Sammellinsen
• Scheinwerfer haben oft Sammellinsen, um parallele Lichtstrahlen zu erzeugen

In der Natur finden wir oft kugelförmige Wassertropfen. Diese wirken wie Sammellinsen mit ihrem typischen, umgekehrten reellen Bild. 🙃

Streulinsen (Zerstreuungslinsen oder Konkavlinsen)

Im Gegensatz zu den Sammellinsen fokussieren die Streulinsen die parallelen Lichtstrahlen nicht, sondern sie zerstreuen sie in alle Richtungen. Die Strahlen verlaufen radial, als kämen sie aus einem virtuellen Brennpunkt heraus.

Je näher dieser virtuelle Brennpunkt an der Linsenebene ist, desto kleiner ist die virtuelle Brennweite \(f\), die in der Linsengleichung mit negativem Vorzeichen eingesetzt wird.

Streulinsen finden wir in fast allen optischen Geräten. Ihr wichtigstes Anwendungsbeispiel ist aber die Brille oder Kontaktlinse für Kurzsichtige. Sie erzeugt zwar ein leicht verkleinertes Bild, erhöht aber die Brennweite der Augenlinse, die bei dieser Sehschwäche zu klein ist.

Das typische Bild der Streulinse ist aufrecht, verkleinert und zeigt damit mehr von der Umgebung, ähnlich wie der Konvexspiegel. Die Streulinse wird deshalb auch im Türspion eingesetzt, so dass durch eine kleine Öffnung möglichst viel von der anderen Seite gezeigt werden kann.

Fresnel-Linsen

Der französische Physiker Augustin Jean Fresnel (1788 – 1827) entwickelte 1822 eine flache Sammellinse für Leuchttürme, die fortan als Fresnel-Linse benannt wurde.

Im 19. Jahrhundert war bekannt, dass eine Sammellinse radial verlaufende Strahlen zu parallelen Lichtstrahlen bündeln kann, so dass der Lichtstrahl sehr weit reichen kann, ohne grosse Verluste an Lichtintensität zu erleiden: Eine ideale Anwendung für Leuchttürme, deren Strahl möglichst weit reichen sollte.

Das Problem der Sammellinse ist aber, dass sie in der Mitte dicker sein muss. Grosse Linsen aus Glas werden dadurch sehr dick und massiv, was zu praktischen Problemen führt. Fresnels Erfindung machte aus der bauchigen Sammellinse eine flache, gestufte Linse.

Fresnel-Linsen sind flache Linsen, deren “gerippte” Oberfläche speziell gefertigt ist. Die Lichtstrahlen treffen auf die unebene Oberfläche so auf, dass sich die Linse wie eine Sammel- oder Streulinse mit Brennpunkt verhält.

Linsengleichung

Egal ob Sammel- oder Streulinse, die Linsengleichung gilt für beide Arten. Sie verknüpft die Abstände von Gegenstand (Gegenstandsweite \(g\)) und Bild (Bildweite \(b\)) mit der Brennweite der Linse \(f\):

\[ \frac{1}{f} = \frac{1}{g} + \frac{1}{b} \]

Mit Hilfe dieser Gleichung können wir z.B. berechnen, wo wir den Schirm haben müssen, um das scharfe reelle Bild einer Sammellinse aufzufangen. Sie erklärt uns auch, warum unsere Augenlinse eine variable Brennweite haben muss, um Gegenstände in verschiedenen Abständen scharf sehen zu können.