Inhalt
Das Wichtigste in Kürze
Wenn das Licht an der Grenzfläche zweier transparenter Medien von einem Medium in ein anderes übertritt, erfolgt Brechung des Lichtstrahls. Sie ist eine direkte Folge der unterschiedlichen Wellengeschwindigkeiten des Lichts in den beiden Medien.
Das Brechungsgesetz sagt uns, unter welchem Winkel ein Strahl gebrochen wird. Dabei ist \(\alpha_1\) der Einfallswinkel zum Lot auf die Grenzfläche im Medium 1 (Brechungsindex \(n_1\)) und \(\alpha_2\) der Brechungswinkel im Medium 2 mit Brechungsindex \(n_2\):
\[ \frac{\sin(\alpha_1)}{\sin(\alpha_2)} = \frac{n_2}{n_1} \]
Trifft der Strahl senkrecht auf die Grenzfläche (Einfallswinkel \(\alpha_1 = 0^\circ\)), dann ist der Brechungswinkel ebenfalls \(\alpha_2 = 0^\circ\).
Je grösser der Unterschied der beiden Brechungsindizes, desto stärker der Knick. Der Winkel zum Lot ist umso grösser, je schneller das Licht im Medium ist und umso kleiner, je stärker die Verlangsamung des Lichts ist.
Tutorial Videos
(Es gibt leider keine Tutorial Videos zu diesem Thema)
Häufigste Fragen

Die Lichtbrechung bzw. die Brechung des Lichts (auch Refraktion genannt) ist ein typisches Wellenphänomen, das auftritt, wenn eine Welle am Übergang in ein anderes Medium ihre Wellengeschwindigkeit ändert. Brechung kommt bei allen Arten von Wellen vor: Licht, Schallwellen, Wasserwellen, Erdbebenwellen etc.
Da die Ausbreitungsgeschwindigkeit des Lichts in Luft und Wasser unterschiedlich sind, bricht das Licht am Übergang von Luft zu Wasser oder umgekehrt.
Die Lichtbrechung ist die Grundlage für Linsen, mit welchen Lichtstrahlen gezielt umgelenkt werden können. Im nachfolgenden Bild sehen wir den Effekt der zweifachen Brechung an der Grenzfläche Luft zu Wasser und Wasser zu Luft. Die Wassertropfen werden zu Sammellinsen und es entsteht ein reelles, umgekehrtes Bild des Hintergrunds.

Fermat: “Der Lichtstrahl wählt jenen Weg, für welchen er zwischen zwei Punkten eine extremale Zeit benötigt (maximal oder minimal).”
Brechung, erklärt mit dem Fermat’schen Prinzip
Gemäss dem Fermat’schen Prinzip löschen sich alle Lichtwellen gegenseitig aus, ausser diejenigen, die einen extremalen Weg einnehmen. Wir vereinfachen das Prinzip und beschränken uns auf zeitlich kürzesten Weg.
Wir betrachten dazu folgendes Beispiel: Ein Strandwächter erkennt eine ertrinkende Person und muss sie möglichst schnell erreichen. Welchen Weg sollte der Strandwächter einnehmen? Wir betrachten die folgenden 3 Extremfälle:
- Er ist auf Sand gleich schnell wie im Wasser
- Er ist auf Sand 1000 mal schneller als im Wasser
- Er ist im Wasser 1000 mal schneller als auf dem Sand

- Wenn er gleich schnell ist, egal ob auf Sand oder im Wasser, dann ist der kürzeste Weg auch der Schnellste. Deshalb müsste er die direkte Linie einschlagen.
- Wenn er im Wasser unglaublich langsam ist, dann kann er einen längeren Weg auf Sand einnehmen, muss aber den Weg im Wasser so kurz wie möglich halten. Der kürzeste Wasserweg gilt für einen Winkel (zum Lot) der 0° beträgt. Dafür ist der Winkel auf der Sandseite gross.
- Im dritten Extremfall ist er auf dem Sand extrem langsam, dafür im Wasser sehr schnell. Hier müsste er den Sandweg minimal halten und mehr Wasserweg in Kauf nehmen. Der Winkel auf der Sandseite ist 0° und auf der Wasserseite ist er gross.
Es ist klar, dass diese drei Fälle unrealistisch sind. Vermutlich ist der Strandwächter auf Sand etwa zwei mal schneller als im Wasser, d.h. er wird einen etwas längeren Sandweg und einen nicht allzu langen Wasserweg wählen. Wir wissen aber jetzt schon, dass der Winkel (zum Lot) auf der Sandseite grösser sein wird, als auf der Wasserseite.

Image by Falco Ermert, licensed under CC BY-SA 2.0
Der schnellste Weg und damit optimale Weg könnte wie oben dargestellt aussehen. Er ist abhängig von den einzelnen Geschwindigkeiten auf Sand bzw. auf Wasser.
Je schneller der Strandwächter auf Sand ist (im Vergleich zu Wasser) desto mehr Sandweg wird er wählen. Es folgt daraus ein grösserer Winkel (zum Lot) auf der Sandseite und ein kleinerer Winkel auf der Wasserseite.
Beim Licht ist es genau gleich. Der Lichtstrahl ändert seine Richtung, sobald er im anderen Medium eine andere Geschwindigkeit hat: Der Strahl bricht in einem Knick. 😎
Im langsameren Medium ist der Weg kürzer, d.h. der Winkel (zum Lot) kleiner. Im schnelleren Medium ist der Weg länger und damit der Winkel (zum Lot) grösser.

Image by Zátonyi Sándor, licensed under CC BY-SA 3.0
Im Bild oben sehen wir, wie der Lichtstrahl beim Eintreffen ins Glas einen charakteristischen “Knick” macht und seine Richtung ändert.
Der Einfallswinkel (zum Lot) ist in der Luft grösser als der entsprechende Winkel im Glas. Dieser “Knick” ist eine Folge des Fermat’schen Prinzips und der unterschiedlichen Geschwindigkeiten des Lichts in den Medien Luft und Wasser. Gemäss diesem Gesetz bleibt durch Auslöschung der Wellen nur das Licht als Strahl übrig, das dem Weg mit minimaler Laufzeit entspricht.
Beispiel
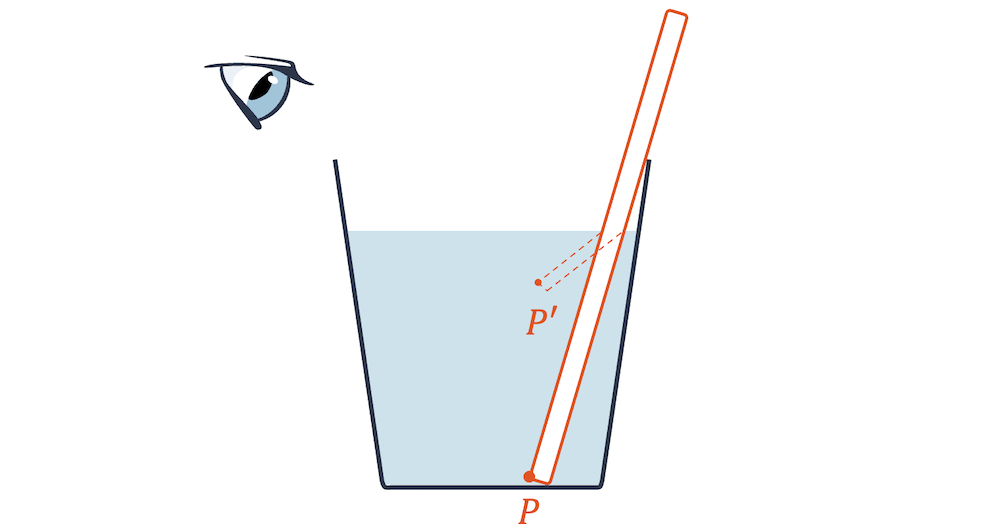

Image by Iain Watson, shared on Flickr
“Je grösser der Brechungsindex, desto langsamer ist das Licht im entsprechenden Medium.”
Lichtgeschwindigkeit und Brechungsindizes
Mit dem Brechungsindex können wir angeben, wie stark das Licht durch das Medium abgebremst wird.
Ist der Brechungsindex \(n_1=1\) bedeutet das maximale Lichtgeschwindigkeit \(c_0\), wie im Vakuum:
\[ c_1 = \frac{c_0}{n_1} = 2.998 \cdot 10^8\,\text{m/s} \]
In einem Material, wie z.B. Wasser \(n_2 = 1.33 \) ist die Lichtgeschwindigkeit kleiner:
\[ c_2 = \frac{c_0}{n_2} = \frac{2.998 \cdot 10^8}{1.33}\,\text{m/s} = 2.25 \cdot 10^8\,\text{m/s} \]
Je grösser der Brechungsindex \(n\), desto langsamer ist das Licht im entsprechenden Medium.
Jetzt ist der Brechungsindex v.a. abhängig vom Material, aber er ist auch in kleinem Masse abhängig von der Frequenz und damit der Wellenlänge \(\lambda\) (Farbe des Lichts). In Quarzglas gilt beispielsweise:
- rotes Licht hat einen Brechungsindex von \(n >1.45\)
- blaues Licht hat einen Brechungsindex von \(n = 1.47\)
- alle anderen Farben haben einen Brechungsindex zwischen diesen beiden Extremen
Die Brechung wird für blaues Licht stärker sein, als für rotes Licht. Auf diese Weise kann weisses Licht an einem Prisma in seine Bestandteile aufgefächert werden.

Brechungsgesetz
In der nachfolgenden Grafik sind drei Fälle von Brechung dargestellt. Wir erkennen sofort, dass das obere Medium das schnellere Medium sein muss, weil dort die Winkel zum Lot grösser sind. Das untere Medium verlangsamt das Licht stärker und hat deshalb einen grösseren Brechungsindex.
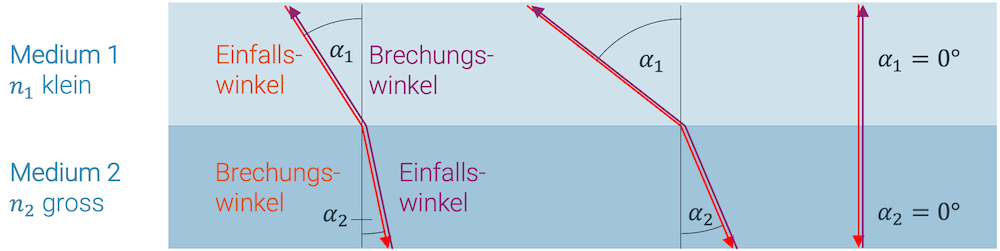
Ganz links ist der Einfallswinkel \(\alpha_1\) noch klein. Im langsameren Medium unten ist der Brechungswinkel \(\alpha_2\) noch kleiner.
In der Mitte wird der Knick deutlicher, weil \(\alpha_1\) etwa doppelt so gross ist wie links. Der Brechungswinkel \(\alpha_2\) ist ebenfalls fast doppelt so gross, wie der Brechungswinkel links.
Wir bemerken deshalb: Das Verhältnis der beiden Winkel scheint gleich zu bleiben. Je grösser der eine Winkel, desto grösser der andere Winkel und der Knick wird deutlicher.
Ganz rechts haben wir einen Einfallswinkel von 0°. Der Brechungswinkel ist auch 0° und wir sehen keinen Knick. Das Verhältnis der beiden Winkel wäre hier auch bewahrt!
“Je grösser sich die beiden Brechungsindizes unterscheiden, desto stärker ist der Knick. Ein Übergang in ein anderes Medium mit (fast) gleichem Brechungsindex findet praktisch ohne Brechung statt.”
Der niederländische Astronom und Mathematiker, Willebrord van Roijen Snell (lateinisch Snellius, 1580 – 1626) fand die Gesetzmässigkeit für das Verhältnis der beiden Winkel. Statt dem direkten Verhältnis der beiden Winkel ist es das Verhältnis der Funktionswerte der Sinus-Funktion beider Winkel:
Brechungsgesetz nach Snellius:
\[ \frac{\sin(\alpha_1)}{\sin(\alpha_2)} = \frac{n_2}{n_1} \]
Dabei sind \(n_1\) und \(n_2\) die Brechungsindizes von Medium 1 bzw. Medium 2. Du kannst dir einfach merken, dass Winkel und Brechungsindizes in der Gleichung übers Kreuz verteilt sind.
Beachte, dass das Gesetz für beide Laufrichtungen des Lichts gilt: Der Winkel \(\alpha_1\) ist der Einfalls- oder Brechungswinkel im Medium 1, je nach Laufrichtung.
Aus dem Beispiel mit dem Strandwächter (weiter oben) ist uns klar, dass der Knick aufgrund der unterschiedlichen Geschwindigkeiten folgt. Hätten wir in beiden Medien die gleiche Geschwindigkeit (\(n_1 = n_2 \)), dann sind die beiden Winkel gleich und wir haben keinen Knick. Je grösser der Unterschied zwischen den beiden Brechungsindizes ist, desto stärker ist der “Knick”.
Beachte: Im Extremfall kann der grössere Winkel im schnelleren Medium 90° erreichen. In diesem Fall kann der Lichtstrahl gar nicht mehr aus dem langsamen Medium austreten und es tritt die sog. Totalreflexion ein. 😮
Beispiel
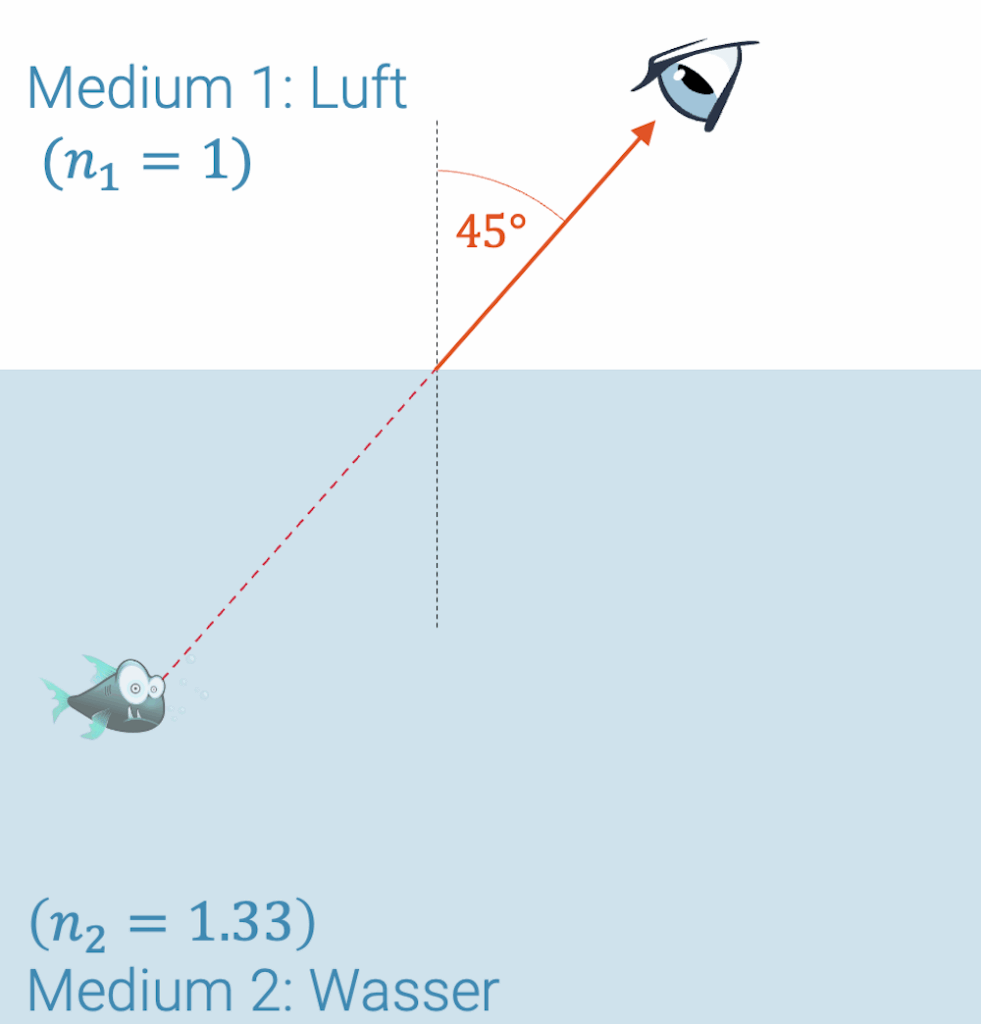

Wir können die Brechung mit einem einfachen Experiment demonstrieren: Eine Lichtquelle ist in gefärbtem Wasser eingetaucht. Die Lichtstrahlen sind hier durch Streuung an einer Rückwand sichtbar gemacht.
Der erste Strahl tritt mit Einfallswinkel 0° auf die Grenzfläche und wird nicht gebrochen: Er tritt aus mit einem Brechungswinkel von ebenfalls 0°.
Ab dem zweiten Strahl erkennen wir die Brechung mit einem grösseren Winkel in der Luft als im Wasser. Danach tritt Totalreflexion ein und der Lichtstrahl vermag nicht mehr aus dem Wasser auszutreten.
Sonne nach dem Sonnenuntergang
Ein interessanter Effekt der Lichtbrechung ist in der nachfolgenden Grafik zu sehen: Obwohl die Sonne schon untergegangen ist und wir eigentlich keine direkten Sonnenstrahlen mehr empfangen sollten, sehen wir die Sonne, oder zumindest einen Teil davon immer noch am Horizont.
Der Grund ist die Brechung in der Atmosphäre. Die Luft hat zwar einen Brechungsindex, der sehr nahe bei 1 ist. doch das Licht ist trotzdem ganz leicht abgebremst durch die Interaktion mit ihr. Die Atmosphäre wird mit kleiner werdenden Höhe immer dichter und damit steigt der Brechungsindex stetig an.
Der Lichtstrahl wird deshalb gebogen und die echte Sonne ist bereits schon hinter dem Horizont. Wir bemerken das aber nicht, weil wir immer davon ausgehen, dass Lichtstrahlen gerade verlaufen. Wir sehen ihr virtuelles Bild am Horizont. Die effektiven Lichtstrahlen verlaufen aber “quasi ums Eck”. 😎

Herleitung des Brechungsgesetzes
Licht, das im Medium 1 auf eine Grenzfläche trifft, verhält sich wie eine Wellenfront mit der Wellenlänge \(\lambda_1\). Die Wellenfront trifft unter dem allgemeinen Einfallswinkel \(\alpha_1\) ein.
Da der Brechungsindex von Medium 2 grösser ist, als derjenige von Medium 1 (\(n_2 > n_1\)), ist die Welle im Medium 2 langsamer. Die regelmässig auf die Grenzfläche auftreffenden Wellenberge und -täler pflanzen sich im anderen Medium fort.
Durch die kleinere Wellengeschwindigkeit sind die Wellenberge und -täler aber näher zusammengerückt: Die Wellenlänge im Medium 2 ist kürzer als im Medium 1 (\(\lambda_2 < \lambda_1\)).
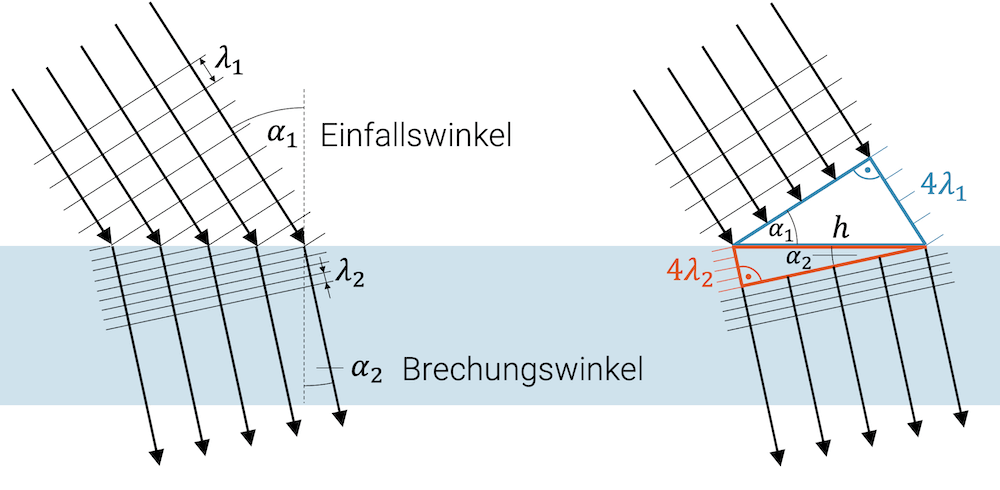
Betrachte nun die beiden rechtwinkligen Dreiecke in der Grafik rechts. Das blaue Dreieck hat eine Hypothenuse \(h\) und eine Gegenkathete mit der Länge von vier Wellenlängen \(4 \lambda_1\). Für den Einfallswinkel \(\alpha_1\) gilt deshalb:
\[ \sin(\alpha_1) = \frac{4 \lambda_1}{h} \]
Da der erste Strahl von links genau vier Wellenlängen früher auf die Grenzfläche auftrifft als der fünfte Strahl, ist er im Medium 2 auch schon vier Wellenlängen voraus, wenn der fünfte Strahl erst beginnt.
Die Gegenkathete im roten Dreieck beträgt ebenfalls vier Wellenlängen \(4 \lambda_2\) und es gilt analog:
\[ \sin(\alpha_2) = \frac{4 \lambda_2}{h} \]
Lösen wir die beiden Ausdrücke nach \(h\) auf, erhalten wir:
\[ h = \frac{4 \lambda_1}{\sin(\alpha_1)} = \frac{4 \lambda_2}{\sin(\alpha_2)} \]
Wir wissen, dass die Lichtgeschwindigkeit \(u_1\) im Medium 1 der Lichtgeschwindigkeit im Vakuum entspricht, die um den Faktor des Brechungsindex’ \(n_1\) verkleinert ist:
\[ u_1 = \frac{c}{n_1} \]
Ab dem Zeitpunkt, in welchem der erste Strahl von links auf die Grenzfläche trifft, verstreicht eine gewisse Zeit, bis auch der fünfte Strahl die Grenzfläche erreicht. Wir geben vor, diese Zeit zu kennen und schreiben für sie einfach \(\Delta t\).
Da die Welle in der Zeit \(\Delta t\) genau vier Wellenlängen \(4 \lambda_1\) kommt, können wir für die Wellengeschwindigkeit schreiben:
\[ u_1 = \frac{4 \lambda_1}{\Delta t} \]
Wir setzen beide Ausdrücke für die Wellengeschwindigkeit \(u_1\) gleich:
\[ \frac{c}{n_1} = \frac{4 \lambda_1}{\Delta t} \]
Nun können wir die obige Gleichung nach \(4 \lambda_1\) auflösen. Das Gleiche tun wir analog für das Medium 2. Wir erhalten somit:
\[ 4 \lambda_1 = \frac{c}{n_1} \cdot \Delta t \qquad \textrm{und} \qquad 4 \lambda_2 = \frac{c}{n_2} \cdot \Delta t \]
Eingesetzt in die Gleichung für die Hypotenuse ergibt:
\[ h = \frac{c \cdot \Delta t}{n_1 \cdot \sin(\alpha_1)} = \frac{c \cdot \Delta t}{n_2 \cdot \sin(\alpha_2)} \]
Nun lassen wir \(h\) weg, dividieren die Gleichung durch die Lichtgeschwindigkeit \(c\) und die Zeitperiode \(\Delta t\), so dass sie sich herauskürzen. Dann multiplizieren wir mit \(n_2\) und mit \(sin(\alpha_1)\). Wir erhalten so das Brechungsgesetz 👍
\[ \frac{\sin(\alpha_1)}{\sin(\alpha_2)} = \frac{n_2}{n_1} \]
Adaptive Optik in der Astronomie
Druck und Temperatur der Luft unterliegen Schwankungen. Diese Schwankungen machen, dass Luftströmungen und Turbulenzen entstehen und dass der Brechungsindex der Luft andauernd verändert wird. Lichtstrahlen können in der Atmosphäre eigentlich nie ganz gerade verlaufen. Sie werden durch diese Schwankungen andauernd gebrochen.
Wir kennen das auch aus eigener Erfahrung, wenn wir das Flimmern der Luft sehen.
Dieses Flimmern ist in der Astronomie ein Problem, weil die kleinen Sterne durch diese Schwankungen (sog. Luftunruhe) zu tanzen beginnen und dadurch kein ruhiges und scharfes Bild gesehen werden kann. 🌟
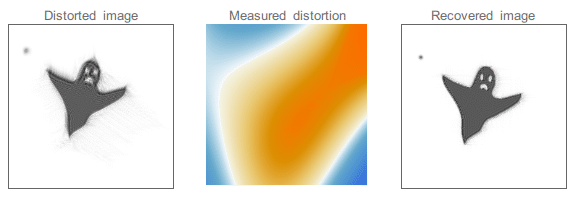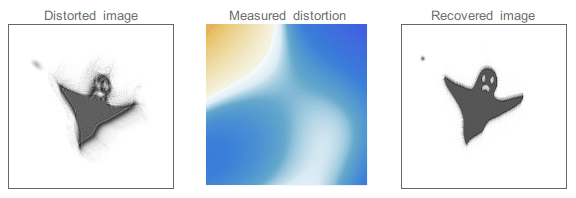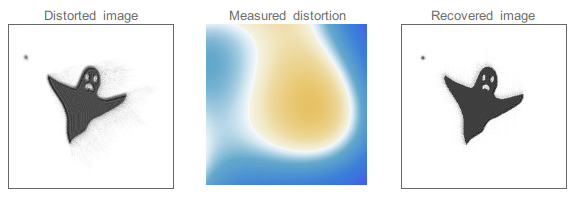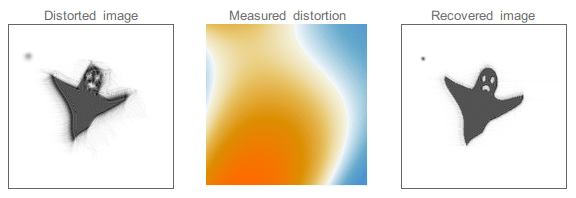
Mit Hilfe der sog. adaptiven Optik können diese Schwankungen festgestellt und korrigiert werden. Mit einem Laserstrahl wird ein künstlicher Leitstern gebildet. Dabei handelt es sich um einen hellen Fleck in der oberen Atmosphäre. Sensoren messen die Abweichungen der Wellenfront, die durch die Luftunruhe entstanden sind und korrigieren den Konkavspiegel des Teleskops.

Image by ESO/B. Tafreshi (twanight.org), CC BY 4.0

Image by ESO/G. Hüdepohl , CC BY 4.0
Simulation
Mit der folgenden Simulation kann die Brechung qualitativ und quantitativ (Brechungsgesetz) ausprobiert werden: OPhysics-Simulation zum Brechungsgesetz
Weitere Videos
Aufgabensammlung
Lernziele
Mini-Test
Um Zugang zum Mini-Test zu kriegen,
musst du vollwertiges Mitglied im Hacker-Club sein.
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt










Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.