Gleitreibung

Die Gleitreibung ist, neben der Rollreibung und Haftreibung, eine der drei Formen der Reibungskraft.

Bei der Gleitreibung reiben zwei Flächen aufeinander, die sich relativ zueinander bewegen. Weil diese Oberflächen nicht ganz glatt sind, entsteht eine Kraft, die sich der Bewegung widersetzt, d.h. sie ist der Bewegung entgegengesetzt.

Beispiele für Gleitreibung:

• Die Fläche der Skier reibt auf dem Schnee
• Die Kufen der Schlittschule gleiten auf dem Eis
• Vorhänge: Gleiter aus Teflon rutschen in einer Aluminiumschiene
• Wir reiben unsere Hände, um sie aufzuwärmen
• Die Bremsbacken drücken auf die Bremsscheibe und wandeln so kinetische Energie in Wärme um
• Ausrutschen auf einer Bananenschale
• Vollbremsung eines Autos mit blockierten Rädern
• Gleitlager

Die Gleitreibung ist deutlich grösser als die Rollreibung und ist deshalb für die Fortbewegung ungeeignet, ausser auf Eis und Schnee.

Die Gleitreibung ist kleiner als die Haftreibung. Wir können das beobachten, dass ein Objekt an einer schiefen Ebene ungestört haften kann. Wird es aber z.B. durch eine leichte Erschütterung gestört, fängt es an zu gleiten und stoppt dann nicht mehr.

Wenn die Gleitreibung ungewollt ist und nicht verhindert werden kann, empfiehlt sich die Wahl von gut gleitenden Materialien (z.B. Teflon) oder der Einsatz von Schmiermitteln. Vielleicht kann die Normalkraft reduziert werden, was direkt zu einer Reduktion der Gleitreibungskraft führt.

Abhängigkeit von der Normalkraft

Die Gleitreibungskraft \(F_R\) ist proportional zur Normalkraft \(F_N\). Je stärker die Flächen aufeinander drücken, desto grösser ist die Gleitreibungskraft.

Wenn wir beispielsweise mit Schleifpapier ein Stück Holz schleifen, so bringt es nicht viel, wenn wir das Stück Holz nur leicht “streicheln”. Das Schleifpapier muss mit einem gewissen Druck angesetzt werden. Je grösser dieser Druck ist, desto grösser ist die Reibungskraft, die sich der Bewegung widersetzt und desto strenger wird das Schleifen.

Die Gleitreibungskraft ist auch abhängig von den Materialien und der Beschaffenheit der Oberflächen. Diese Eigenschaften werden im Gleitreibungskoeffizienten \(\mu_G\) zusammengefasst:

\[ F_R = \mu_G \cdot F_N \]

Der Gleitreibungskoeffizient \(\mu_G\) kann aus Tabellen abgelesen werden. Er berücksichtigt die Beschaffenheit der beiden Oberflächen:

• Glatte, gut gleitende Oberflächen: \(\mu_G\) klein (z.B. Geschmierter Stahl auf Stahl: \(\mu_G=0.011\))
• Raue Oberflächen: \(\mu_G\) gross (z.B. Gummi auf Asphalt: \(\mu_G=0.51\))

Beispiel

Das Vorderrad eines Autos (\(m=1.8\,\text{t})\) überträgt einen Viertel der Gewichtskraft. Es dreht im Schnee durch. Wie viel beträgt die Gleitreibungskraft und wie ist die Gleitreibungskraft am Rad gerichtet (Gleitreibungskoeffizient: \(\mu_G=0.15\))

Lösung

Die Gleitreibungskraft ist abhängig von der Normalkraft, die die beiden Flächen zusammendrückt. Diese entspricht einem Viertel der Gewichtskraft, d.h. \[ F_N=\frac{F_g}{4}= \frac{1}{4} \cdot m \cdot g \] \[ F_N = \frac{1}{4} \cdot 1’800\,\text{kg} \cdot 9,81\,\frac{\text{m}}{\text{s}^2} = 4’415\,\text{N} \] Jetzt setzen wir dieses Zwischenresultat in die Gleichung für die Gleitreibung ein: \[ F_R = \mu_G \cdot F_N = 0.15 \cdot 4’415\,\text{N} = \underline{662\,\text{N}} \] Diese Reibungskraft ist der Drehrichtung des Rads entgegengesetzt, d.h. wenn das Rad sich im Uhrzeigersinn dreht, wirkt die Kraft unten am Rad nach vorne, das Rad bremsend.

Beachte: Gemäss Newtons Drittem Gesetz wirkt das Rad mit der gleich grossen, aber gerade entgegengesetzten Kraft auf den Boden, d.h. der Boden erfährt eine Kraft nach hinten.

Gleitreibung an der schiefen Ebene

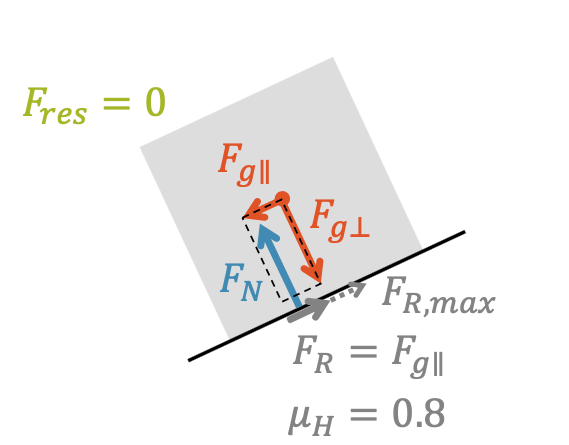
Die Gleitreibung ist meistens kleiner als die Haftreibung bei gleichen Materialien und gleicher Normalkraft. Wir können das an der schiefen Ebene gut erkennen.

Ein ruhender Klotz hält durch Haftreibung an der schiefen Ebene, d.h. er ist im Kräftegleichgewicht und die Haftreibungskraft ist gleich der Parallelkomponente der Gewichtskraft \(F_{g \parallel}\).

Weil sich alle Kräfte gegenseitig aufheben, haben wir eine verschwindende resultierende Kraft \(F_{res}0=\), d.h. wir sind im Kräftegleichgewicht.

Überschreiten wir die Obergrenze der Haftreibung, kommt der Klotz ins Gleiten.

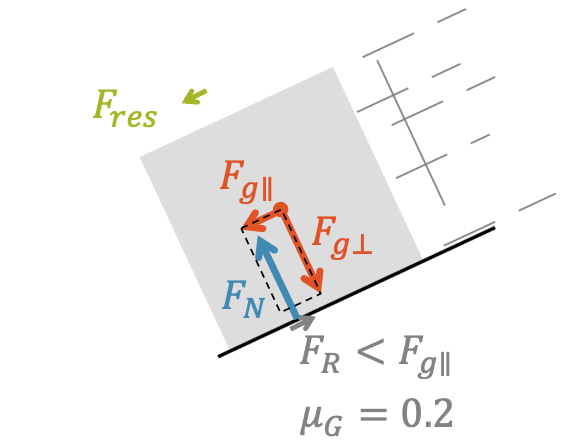
Die Kräftesituation ändert sich. Die Gleitreibung ist bei gleicher Normalkraft aber kleinerem Gleitreibungskoeffizienten \(\mu_G < \mu_H\) nun kleiner als die Haftreibungskraft. Dadurch verlieren wir das Kräftegleichgewicht, denn die Gleitreibungskraft ist kleiner als die Parallelkomponente der Gewichtskraft: \(F_R < F_{g \parallel}\). Wir haben jetzt eine resultierende Kraft \(F_{res}\), die den Klotz den Hang hinunter beschleunigt.

Die Beschleunigung zeigt ebenfalls den Hang hinunter und berechnet sich gemäss Newtons Zweitem Gesetz. Der Klotz gleitet den Hang hinunter und wird dabei immer schneller.

Wenn wir diese Situation auf den Skifahrer übertragen, dann wäre das etwas beängstigend. Allerdings wird der Skifahrer einen weniger steilen Winkel wählen, so dass \(F_R \approx F_{g \parallel}\) er den Hang im Kräftegleichgewicht, d.h. mit konstanter Geschwindigkeit hinunterfahren kann.