Spannarbeit

Das Konzept der Feder kann näherungsweise auf alle elastischen Materialien übertragen werden. Die Spannarbeit führt zu einer elastischen Verformung des Materials bzw. umgekehrt: Jede elastische Verformung bedingt das Verrichten von Spannarbeit.

Zusammenhang mit der potenziellen Energie

Wenn wir eine Feder dehnen oder sie zusammendrücken, geht das nicht von selbst, sondern es muss physikalische Arbeit dafür verrichtet werden. Diese Arbeit führt der Feder Energie zu, die sie als potenzielle Energie speichert. Dabei handelt es sich aber nicht um Lageenergie, sondern um potenzielle Energie aufgrund der Federkraft (Spannenergie).

In der Feder passiert folgendes: Ist die Feder entspannt, hat sie keine potentielle Energie gespeichert. Sie ist energetisch im tiefsten Punkt, der üblicherweise auf null gesetzt wird.

Die Atome bzw. Moleküle sind in einem bestimmten Abstand zu einander. Ändern wir diesen Abstand, spüren wir einen Widerstand, der auf die quantenmechanische Coulombkraft zurück zu führen ist. Beim Zusammendrücken, stossen sich die Elektronen der Atome ab, beim Auseinanderziehen, ziehen sie sich gegenseitig an.

Lassen wir die Feder im gespannten Zustand, so verbleibt die zugeführte Spannarbeit in Form von Spannenergie in der Feder gespeichert. Lassen wir zu, dass sich die Feder wieder entspannt, werden die Atome wieder in den Gleichgewichtszustand gehen und so die gespeicherte Energie als Spannarbeit wieder abgeben. Wir haben dann eine gespannte Feder, die Spannarbeit abgibt und sich dabei entspannt.

Die Spannarbeit berechnet sich wie folgt:

\[ W \;\;=\;\; \frac{1}{2} k s_2^2 \;-\; \frac{1}{2} k s_1^2 \]

Dabei ist die \(k\) die Federkonstante. Die Feder wird von der Ausdehnung \(s_1\) bis zur Ausdehnung von \(s_2\) gespannt. Mit “Ausdehnung” meinen wir die zusätzliche Streckung oder Stauchung im Vergleich zur entspannten Länge der Feder.

Herleitung

Die Kraft unserer Feder folgt dem Hooke’schen Gesetz, d.h. die Federkraft nimmt proportional mit der Ausdehnung \(\Delta s\) zu:

\[ F=k \cdot \Delta s \]

Im \(F\)-\(s\)-Diagramm (Kraft-Weg-Diagramm) ist die Federkraft \(F\) durch eine lineare Funktion mit Steigung \(k\) beschrieben. Je grösser die Federkonstante \(k\), desto steifer die Feder, d.h. desto schneller nimmt die Federkraft zu und wir haben eine grössere Steigung im Kraftverlauf.

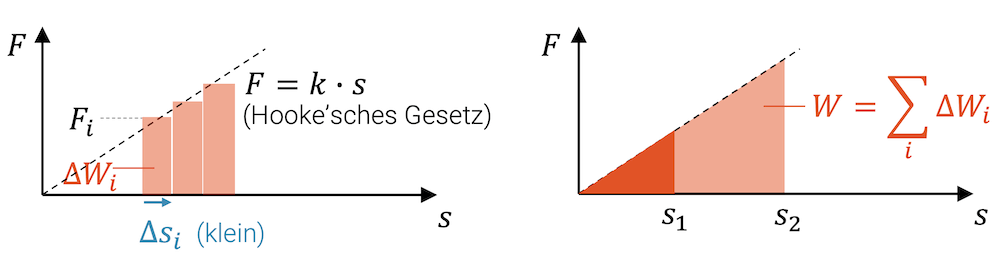
Wenn wir nur eine sehr kleine Wegstrecke \(\Delta s\) dehnen, verändert sich die Kraft auch nur sehr geringfügig. Wir können deshalb näherungsweise annehmen, dass die Kraft \(F_i\) konstant ist. Die Spannarbeit für diese sehr kleine Wegänderung \(\Delta s\) ist demnach:

\[ \Delta W_i=F_i \cdot \Delta s \]

Der kleine Beitrag an Arbeit \(\Delta W_i\) entspricht grafisch der Fläche des kleinen Rechtecks mit Grundseite \(\Delta s\) und Höhe \(F_i\).

Wenn wir die vielen schmalen Rechtecke mit Fläche \(\Delta W_i\) addieren, erhalten wir als Summe die gesamte Spannarbeit \(W\):

\[ W = \sum_i \Delta W_i = \sum_i F_i \; \Delta s \]

Statt der “Treppe” machen wir jetzt die Rechtecke unendlich schmal (\(\Delta s \rightarrow 0\)) und stellen uns vor, wir hätten unendlich viele solcher Rechtecke. Diese unendliche Summe von unendlich dünnen Rechtecken entspricht der Trapezfläche von \(s_1\) bis \(s_2\) bzw. dem entsprechenden Integral:

\[ W = \int_{s_1}^{s_2} F\;ds = \int_{s_1}^{s_2} k \cdot s \; ds = \Big[\frac{1}{2} k s^2\Big]_{s_1}^{s_2} \]

\[ W \;\;=\;\; \frac{1}{2} k s_2^2 \;-\; \frac{1}{2} k s_1^2 \]

Wir können das aber auch geometrisch lösen, indem wir Dreiecksflächen berechnen: Wird die Feder von 0 bis \(s_2\) gestreckt, nimmt die Kraft zu, bis maximal \(F_2=k \cdot s_2\). Die Spannarbeit entspricht der Dreiecksfläche mit der Grundseite \(s_2\) und der Höhe \(F_2\):

\[ W_2 = \frac{1}{2} \cdot F_2 \cdot s_2 = \frac{1}{2} \cdot (k \cdot s_2) \cdot s_2 \]

\[ W_2 = \frac{1}{2} k s_2^2 \]

Gleiches gilt natürlich auch für eine Spannung der Feder von 0 bis \(s_1\):

\[ W_1 = \frac{1}{2} k s_1^2 \]

Wenn wir eine bereits bis \(s_1\) gespannte Feder zusätzlich von \(s_1\) bis \(s_2\) spannen, entspricht die zusätzlich verrichtete Spannarbeit der Differenz der beiden Spannarbeiten \(W_2\) und \(W_1\), d.h. der Differenz der beiden Dreiecksflächen. Wir erhalten so die Formel für die Spannarbeit:

\[ W \;\;=\;\; W_2 \;-\; W_1 \;\;=\;\; \frac{1}{2} k s_2^2 \;-\; \frac{1}{2} k s_1^2 \]