Inhalt
Das Wichtigste in Kürze
Unter Arbeit verstehen wir in der Physik die Änderung der Energie. Es gibt zwei Hauptformen der Arbeit:
- Mechanische Arbeit
- Elektrische Arbeit
Als elektrische Arbeit bezeichnen wir die Übertragung von Energie über das elektromagnetische Feld, z.B. mit Hilfe eines elektrischen Leiter in einem Stromkreis (siehe auch Poynting-Vektor).
Für die mechanische Arbeit unterscheiden wie die folgenden Formen:
Bei der mechanischen Arbeit wirkt eine Kraft \(\vec{F}\) über eine Wegstrecke \(\overrightarrow{\Delta s}\). Die Arbeit \(W\) berechnet sich mit dem Skalarprodukt der beiden Vektorgrössen:
\[ W=\vec{F} \cdot \overrightarrow{\Delta s} \]
\[ W = F \cdot \Delta s \cdot \cos(\alpha) \]
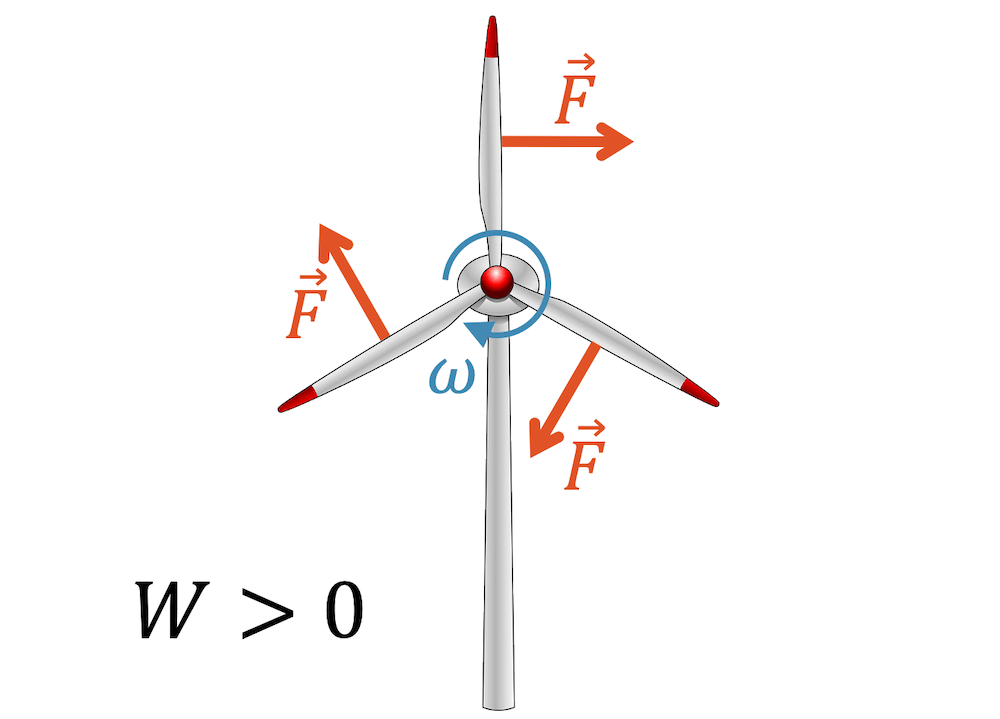
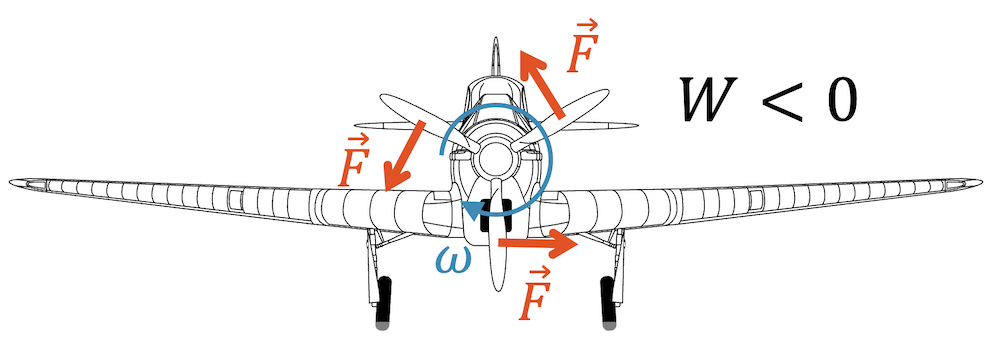
Wenn an einem System Arbeit verrichtet wird, gewinnt es an Energie: \(W\) mit positivem Vorzeichen. Umgekehrt verliert ein System Energie, wenn es selber Arbeit verrichtet (Arbeit mit negativem Vorzeichen):
- \(W>0\) am betrachteten System wird Arbeit verrichtet, es erhält Energie
- \(W<0\) das betrachtete System verrichtet selber Arbeit und gibt dabei Energie ab
Aus dem Skalarprodukt bei der Berechnung der mechanischen Arbeit folgt:
- Kraft \(\vec{F}\) und Wegstrecke \(\overrightarrow{\Delta s}\) sind gleich gerichtet (\(\alpha = 0^\circ\)): \(\;W>0\)
- Kraft \(\vec{F}\) und Wegstrecke \(\overrightarrow{\Delta s}\) sind entgegengesetzt (\(\alpha = 180^\circ\)): \(\;W<0\)
- Kraft \(\vec{F}\) und Wegstrecke \(\overrightarrow{\Delta s}\) stehen senkrecht aufeinander (\(\alpha = 90^\circ\)): \(\;W=0\)
Unter dem Kraftverlauf im Kraft-Weg-Diagramm (F-s-Diagramm) entspricht die Fläche der geleisteten Arbeit:
\[ W = \int F(s) \; ds \]
Weitere Artikel zu diesem Thema:
Tutorial Videos
Häufigste Fragen
Definition
Unter Arbeit verstehen wir in der Physik die Übergabe von Energie von einem System an ein anderes. Bei der mechanischen Arbeit erreichen wir das durch eine Kraft, die über eine Wegstrecke wirkt, wie im nachfolgenden Bild: Das Mädchen lässt die Kraft \(\vec{F}\) wirken und hebt mit ihr die Kiste auf die Höhe \(\overrightarrow{\Delta s}\) auf.
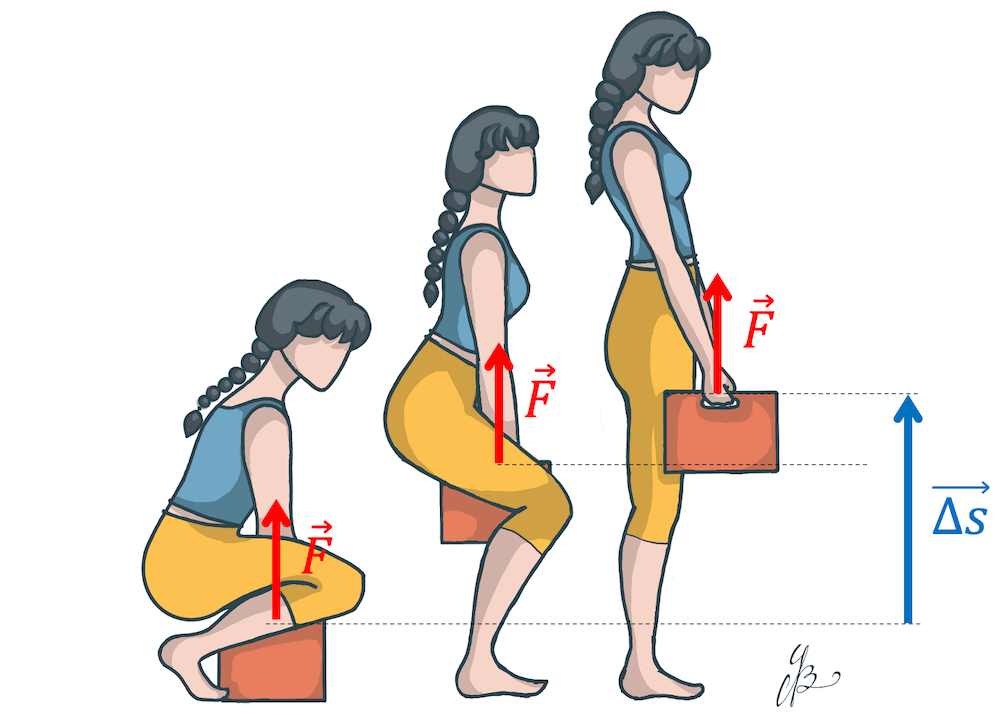
Physikalische Arbeit: \(W\) (engl. “work”)
Einheit: \(\text{J}\) (Joule, übliche Einheit der Energie)
Abgrenzung physikalische Arbeit und Energie
Die physikalische Grösse Arbeit gehört zum Themengebiet der Energie. Energie und Arbeit sind theoretische Konzepte. Es wird unterschieden zwischen der Übertragung und der Speicherung:
- Arbeit = Übertragung von Energie von einem System auf ein anderes
- Energie = gespeicherte Energie in einem System
Abgesehen von dieser Unterscheidung sind in der Physik Arbeit und Energie äquivalent. Deshalb hat die Arbeit in der Physik die Einheit Joule, gleich wie die Energie.
“Energie ist die gespeicherte Fähigkeit, Arbeit zu verrichten, d.h. wenn Arbeit verrichtet wird, wird Energie übertragen.”
Wir unterscheiden folgende Formen von Arbeit:
- Mechanische Arbeit (Hubarbeit, Spannarbeit, Beschleunigungsarbeit und Reibungsarbeit)
- Elektrische Arbeit
Bei der mechanischen Arbeit wirkt eine Kraft über eine bestimmte Weglänge. So wird mechanische Arbeit verrichtet. Je nach Szenario benutzen wir spezifische Bezeichnungen, wie nachfolgend erläutert.
Die zweite Form der Arbeit ist die elektrische Arbeit. Diese kommt dann vor, wenn z.B. ein Gerät mit elektrischem Strom versorgt wird. Das Gerät erhält dabei auch die nötige Energie, die oft elektrische Energie genannt wird. Korrekterweise sollte man hier aber von elektrischer Arbeit sprechen, da es sich um eine Übertragung von Energie handelt und nicht um eine Speicherung von Energie.
Elektrische Energie gibt es auch, aber sie kann nur in Form eines elektrischen Felds in einem Kondensator oder in Form eines magnetischen Felds in einer Spule gespeichert werden. In diesen beiden Fällen ist die Energie wirklich gespeichert. In den meisten Fällen wird die elektrische Energie aber über eine Stromleitung übertragen, d.h. es handelt sich um elektrische Arbeit.
Hubarbeit
Die wohl einfachste Form von mechanischer Arbeit ist die Hubarbeit. Wie der Name sagt, entsteht sie beim Anheben eines Objekts gegen seine Gewichtskraft. Die Arbeit, die dabei verrichtet werden muss, ist dann als potenzielle Energie (Lageenergie) im Objekt gespeichert, denn das Objekt hat nach dem Heben eine grössere Höhe.
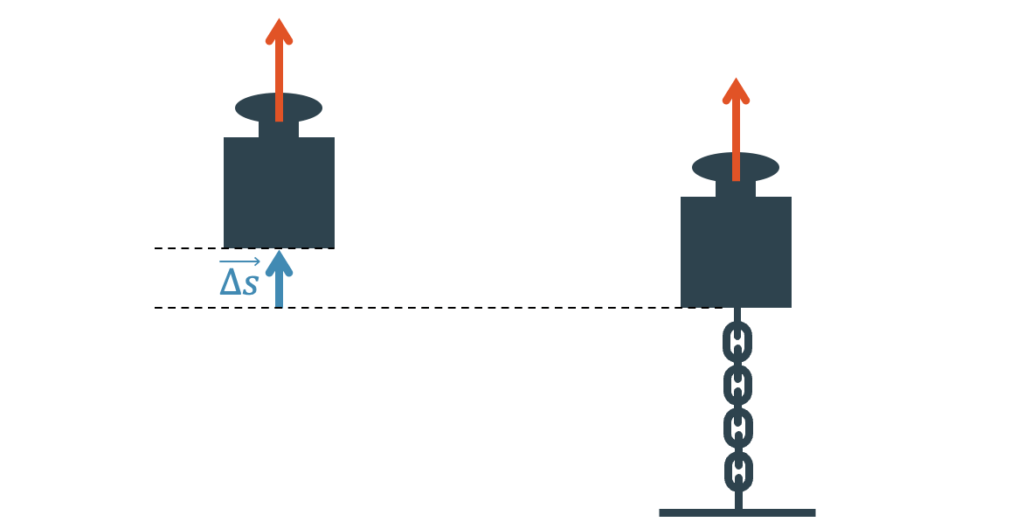
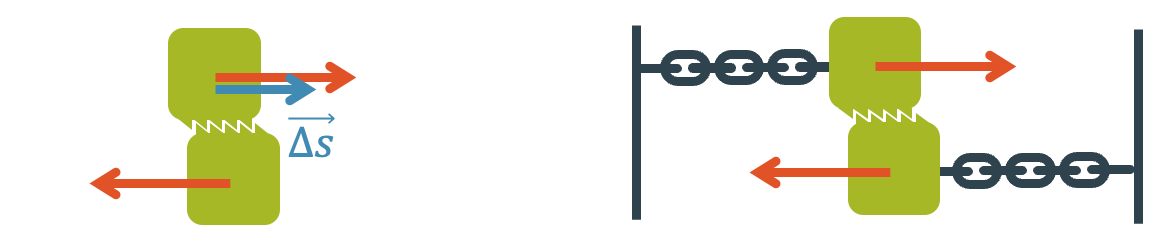
Beachte, dass nicht nur die Kraft wirken muss, sondern dass diese Kraft über eine Wegstrecke \(\Delta s\) wirken muss. Würden wir die Last am Bewegen hindern, indem wir sie am Boden anketten, könnten wir keine Hubarbeit leisten.
Spannarbeit
Dehnen wir eine Feder oder verformen wir ein elastisches Material, geht das nicht ohne Kraft. Die Kraft wirkt zudem über eine kleine Wegstrecke, so dass wir die Voraussetzungen für das Verrichten von Arbeit erfüllt haben.
Die mit der Spannarbeit übertragene Arbeit, wird auch hier in Form von potenzieller Energie in der Feder bzw. im elastischen Material gespeichert.
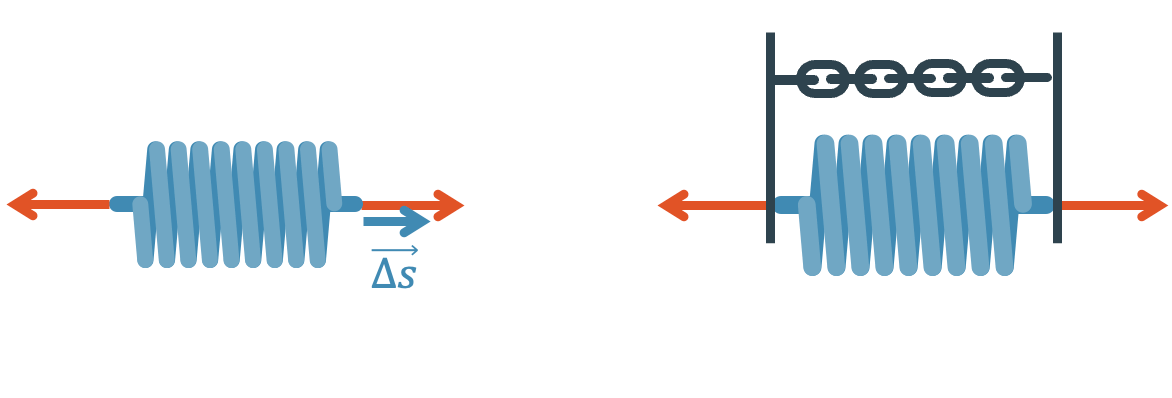
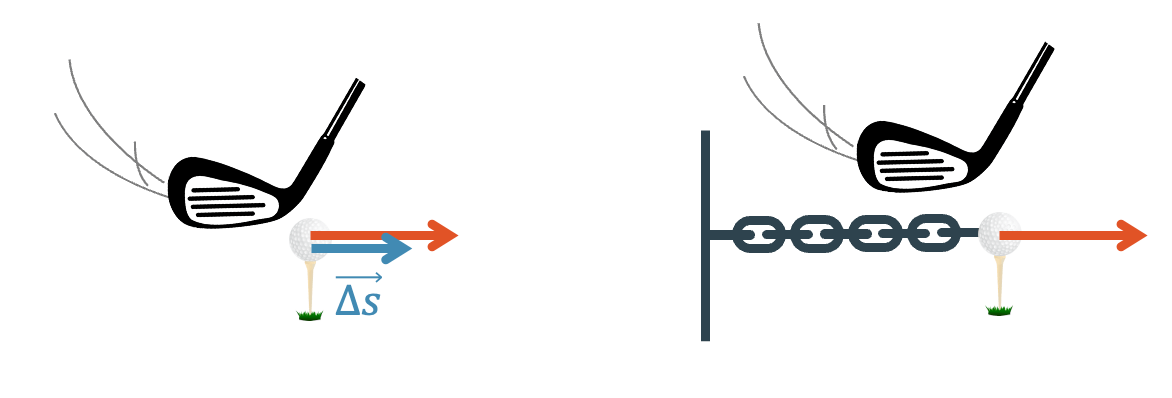
Beschleunigungsarbeit
Wenn wir mit einem Golfschläger für kurze Zeit auf den Golfball mit einer Kraft einwirken, wir dieser in erster Linie beschleunigt. Das Gleiche passiert bei jedem Ballsport, wo ein Ball weggeschossen wird. Die Arbeit, die der Schläger am Ball verrichtet, heisst deshalb Beschleunigungsarbeit.
Die vom Ball erhaltene Arbeit wird in Form von kinetischer Energie (Bewegungsenergie) gespeichert.
Auch wenn die Kraft nur kurze Zeit wirkt, so muss sie unbedingt über eine bestimmte Wegstrecke wirken. Falls wir das z.B. mit einer Kette verhindern, wird der Ball höchstens ein bisschen verformt, aber er kann keine kinetische Energie aufbauen.
Reibungsarbeit
Die Reibungskraft (genauer: Gleit- oder Rollreibung) ist eine bremsende Kraft. Wenn z.B. ein Klotz trotz Reibung verschoben wird, wird die Arbeit, die dabei aufgewendet wird, in thermische Energie umgewandelt, d.h. ungerichtete Teilchenbewegung, die wir als erhöhte Temperatur feststellen können, d.h. die Reibungsfläche wird warm.
Bei allen vorgestellten Formen von mechanischer Arbeit war immer eine Kraft \(F\) und eine Wegstrecke \(\Delta s\) dabei, über welche die Kraft gewirkt hat. Die mechanische Arbeit berechnen wir einfach aus dem Produkt der beiden:
Mechanische Arbeit (Physik) Formel:
\[ W=\vec{F} \cdot \overrightarrow{\Delta s} \]
Es ist klar, dass wir ohne Kraft, keine physikalische Arbeit haben können. Hier sehen wir aber auch, dass ohne Wegstrecke \(\Delta s\) auch keine Arbeit verrichtet wird.
“Eine Kraft ohne Bewegung in Richtung der Kraft kann aus physikalischer Sicht nicht müde machen, weil ohne Wegstrecke die Arbeit null sein muss.”
Das ist nicht selbstverständlich, denn wir werden müde, wenn wir schwere Taschen tragen müssen, selbst dann, wenn wir sie nur einmal ganz kurz anheben mussten.
Alleine das Tragen macht uns müde! Aus physikalischer Sicht wurde aber keine Arbeit geleistet!
Die potenzielle Energie der Tasche bleibt konstant, d.h. wenn die Tasche keine Energie kriegt, hat niemand Arbeit verrichtet!
Elektrische Arbeit
Bei der elektrischen Arbeit wird Energie übertragen (weshalb wir hier von Arbeit reden), aber das geschieht nicht mit einer Kraft über eine Wegstrecke, wie in der Mechanik, sondern auf elektrische Art.
Es muss bei elektrischer Spannung ein elektrischer Strom fliessen. Durch diese Kombination wird im elektromagnetischen Feld Energie transportiert, was mit dem Poynting-Vektor beschrieben werden kann.

Arbeit als Skalarprodukt von Kraft und Wegstrecke
Die folgende Formel für die mechanische Arbeit gilt nur, wenn die Kraft und die Wegstrecke genau gleich gerichtet sind:
\[ W=\vec{F} \cdot \overrightarrow{\Delta s} \]
Wenn wir nämlich die Kraft \(\vec{F}\) und die Wegstrecke \(\vec{\Delta x}\) als Vektoren zeichnen, so könnten die beiden auch unterschiedliche Richtungen haben.
In der nachfolgenden Skizze wird ein Wagen gestossen, wobei die schräge Stosskraft leicht zum Boden zeigt.
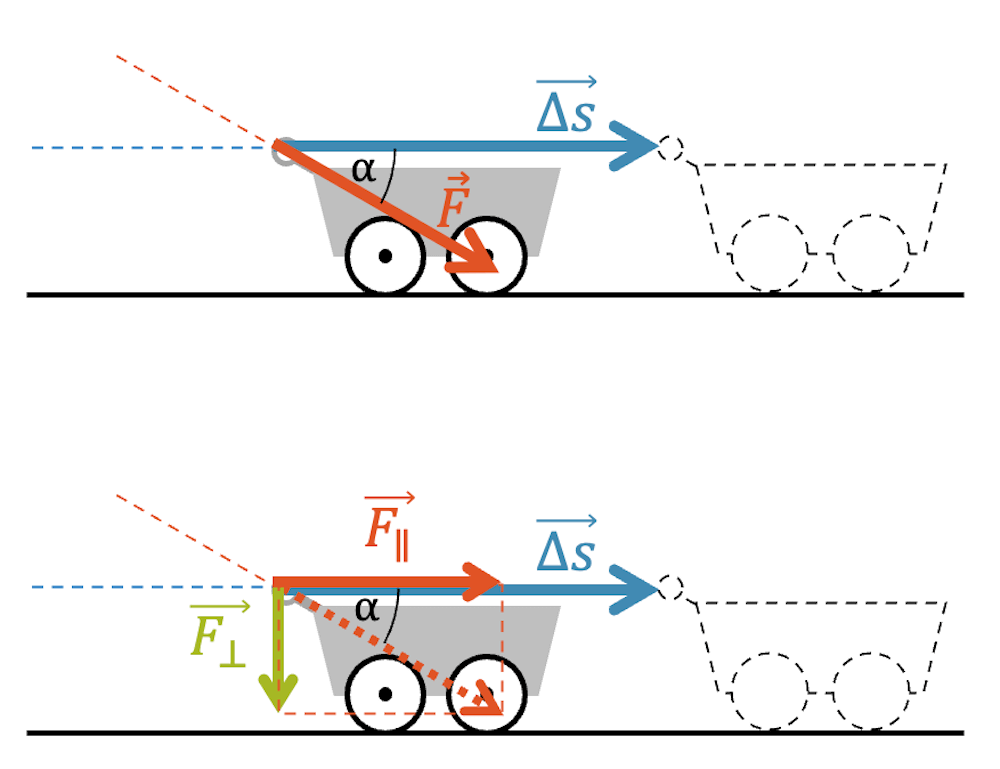
Wenn wir jetzt die Kraft \(\vec{F}\) in zwei Komponenten aufteilen, erhalten wir:
- Parallelkomponente \(\vec{F}_{\parallel}\), die genau gleich gerichtet ist wie \(\vec{\Delta s}\) und somit den vollen Beitrag zur Arbeit leistet
- Senkrechtkomponente \(\vec{F}_{\perp}\), die keinen Beitrag zur Arbeit leistet
Da die Parallelkomponente als einzige einen Beitrag zur Arbeit leistet, können wir schreiben:
\[ W = F_{\parallel} \cdot \Delta s \]
Jetzt können wir die Parallelkomponente \(F_{\parallel}\) mit der Kraft \(F\) ausdrücken:
\[ \frac{F_{\parallel}}{F} = \cos(\alpha) \quad \rightarrow \quad F_{\parallel} = F \cdot \cos(\alpha) \]
Einsetzt erhalten wir:
\[ W = F \cdot \Delta s \cdot \cos(\alpha) \]
Das Gleiche erhalten wir, wenn wir das Skalarprodukt der beiden Vektoren \(\vec{F}\) und \(\overrightarrow{\Delta s}\) bilden:
\[ W = \vec{F} \cdot \overrightarrow{\Delta s} \]
Wenn die beiden Vektoren genau gleich gerichtet sind, ist der Winkel \(\alpha = 0^\circ\) und der Kosinus davon ist 1, d.h. wir haben dann 100%-ige-Arbeitsleistung der Kraft.
Analog bei entgegengesetzter Richtung mit \(\alpha = 180^\circ\) und \(\cos(180^\circ)=-1\). Hier wird das Vorzeichen der Kraft negativ.
Vorzeichen der physikalischen Arbeit
Aus der allgemeinen Formel für die physikalischen Arbeit:
\[ W = F \cdot \Delta s \cdot \cos(\alpha) \]
erhalten wir die folgenden drei wichtigsten Fälle:
- Kraft \(\vec{F}\) und Wegstrecke \(\overrightarrow{\Delta s}\) sind gleich gerichtet (\(\alpha = 0^\circ\)): \(\;W>0\)
- Kraft \(\vec{F}\) und Wegstrecke \(\overrightarrow{\Delta s}\) sind entgegengesetzt (\(\alpha = 180^\circ\)): \(\;W<0\)
- Kraft \(\vec{F}\) und Wegstrecke \(\overrightarrow{\Delta s}\) stehen senkrecht aufeinander (\(\alpha = 90^\circ\)): \(\;W=0\)
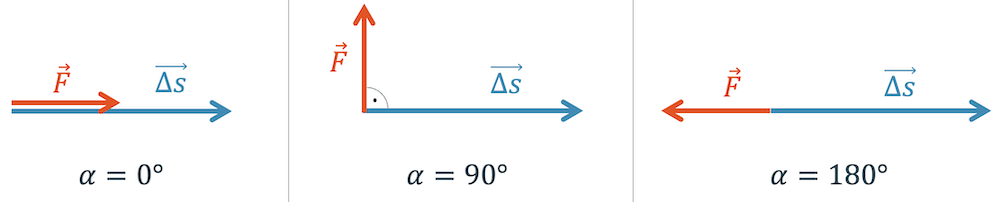
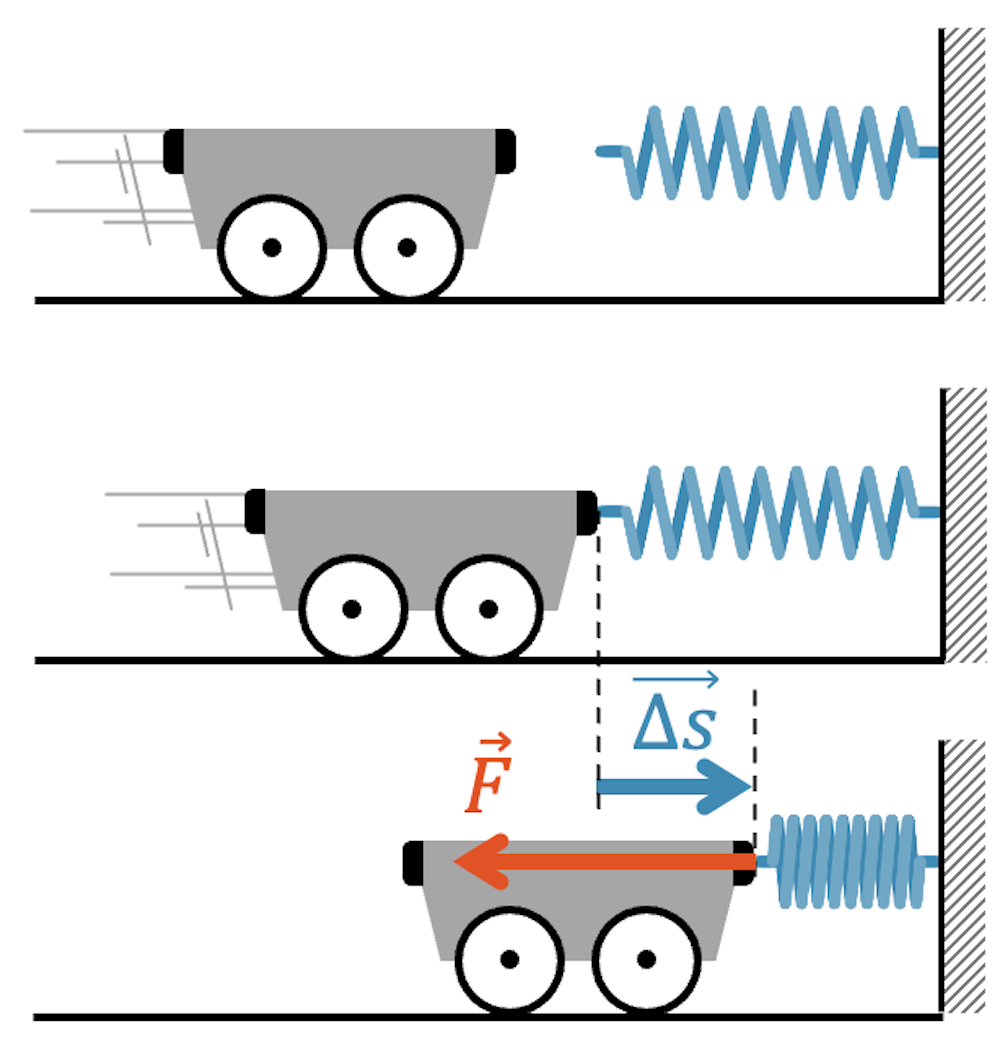
Wir betrachten dazu ein Beispiel: Eine gespannte Feder hat potenzielle Energie gespeichert. Wird die Feder per Knopfdruck freigegeben, so dass sie sich wieder entspannen kann, ist sie in der Lage ihre gespeicherte Energie abzugeben.
Im folgenden Beispiel dehnt sich die Feder aus und beschleunigt den Wagen.
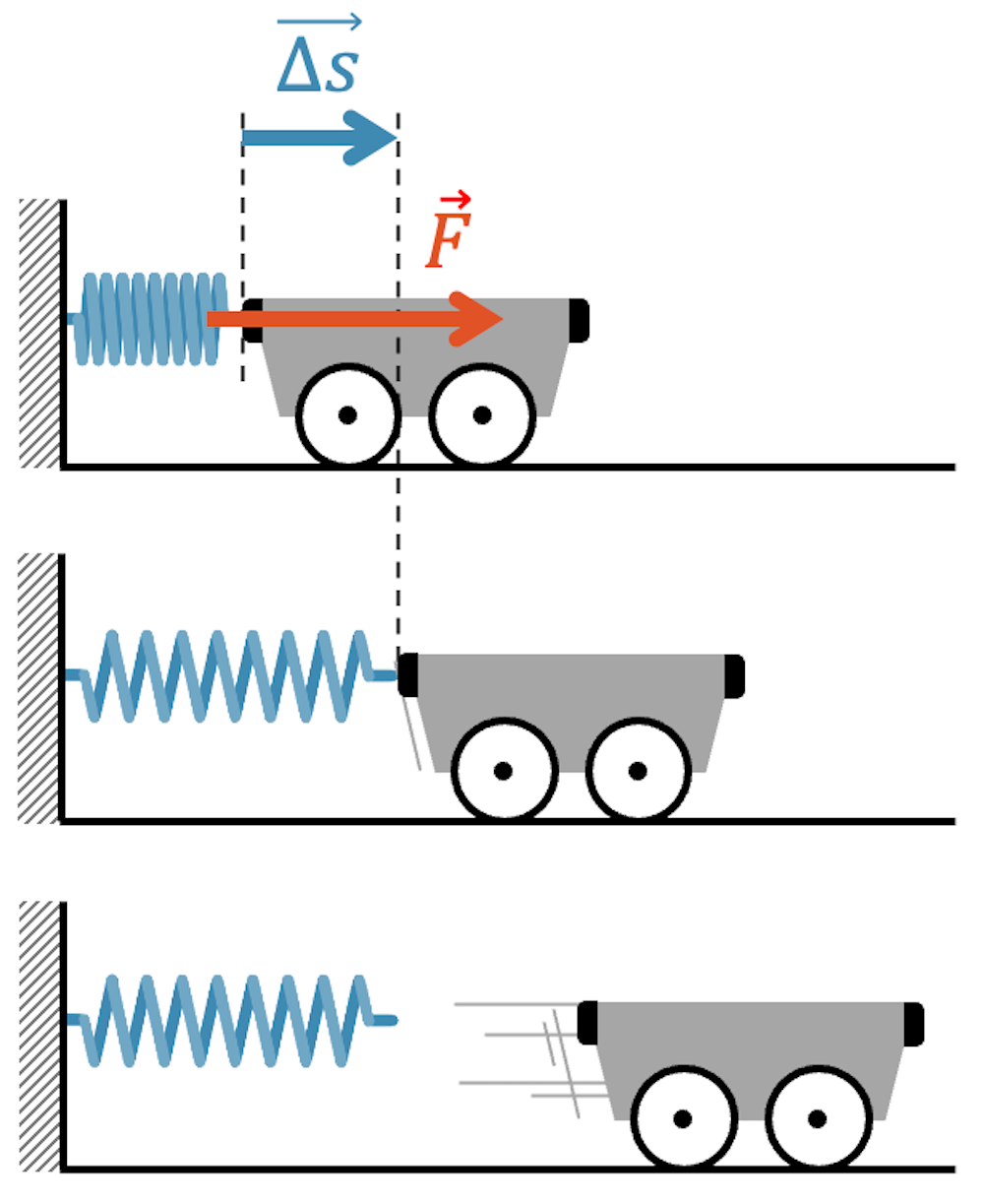
Aus Sicht der Feder gibt sie Spannarbeit ab (\(W<0\)).
Aus Sicht des Wagens, kriegt dieser Beschleunigungsarbeit (\(W>0\)).
Beachte, dass beide Sichtweise das Gleiche beschreiben. Das, was die Feder abgibt, ist das, was der Wagen bekommt.
Aus Sicht des Wagens ist die Federkraft nach rechts gerichtet, gleich gerichtet (\(\alpha = 0^\circ\)) wie die Bewegung selber, so dass wir daraus schliessen können, dass der Wagen damit Arbeit erhält, d.h. positiv ist: \(W>0\)
Wir schauen uns jetzt den umgekehrten Fall an: Der Wagen hat Energie, weil er am Rollen ist (er hat kinetische Energie) und trifft dann auf die noch ungespannte (d.h. energielose) Feder auf.
Beim Auftreffen wird die Federkraft auf den Wagen nach links, also entgegengesetzt (\(\alpha = 180^\circ\)) zur Bewegung. Die Arbeit ist für den Wagen deshalb negativ: \(W<0\)
Der Wagen gibt Arbeit ab an die Feder. An ihm wirkt eine abbremsende Beschleunigungsarbeit und er verrichtet an der Feder eine Spannarbeit, die die Feder zusammenstaucht und in ihr potenzielle Energie speichert.
Beispiel
Kraftwirkung mit/ohne Arbeit
Es gibt auch Fälle, wo zwar eine Kraft über eine Wegstrecke wirkt und trotzdem keinerlei Arbeit geleistet wird! Das ist genau dann der Fall, wenn die Kraft senkrecht auf der Bewegung steht.
Nehmen wir die Formel für die Berechnung der Arbeit:
\[ W = F \cdot \Delta s \cdot \cos(\alpha) \]
Die Arbeit kann null sein, selbst dann, wenn \(F\) und \(\Delta s\) beide nicht null sind. Es reicht, wenn der Kosinus null ist. Der Kosinus ist null für einen Winkel von 90°:
\[ \cos(90°) = 0 \]
Im folgenden Beispiel bewegt sich die Erde um die Sonne auf einer Kreisbahn. Damit ist die Bewegung tangential und die Gravitationskraft zwischen der Erde und der Sonne ist radial, d.h. die Kraft wirkt genau senkrecht zur Bewegung.
Die Arbeit ist null, so dass die Sonne keine Arbeit verrichtet und an der Erde keine Arbeit verrichtet wird. Die Erde behält ihre Bahngeschwindigkeit konstant.
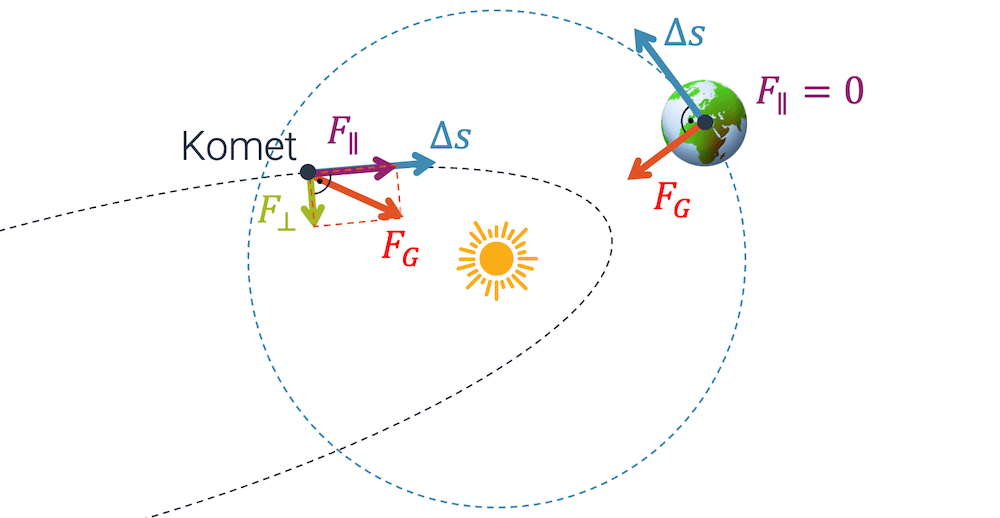
Beim Kometen ist das anders: Die Bahn des Kometen ist sehr elliptisch, so dass die Kraft nicht senkrecht zur Bahngeschwindigkeit sein kann.
Wir können die Kraft aufteilen in zwei Anteile:
- Kraft \(F_{\perp}\) steht senkrecht zur Bewegung und verrichtet damit keine Arbeit
- Kraft \(F_{\parallel}\) zeigt in die gleiche Richtung, wie die Bewegung und verrichtet damit am Kometen Arbeit
Der Komet wird in der Nähe der Sonne schneller, weil an ihm die Sonne mit einer Beschleunigungsarbeit wirkt (siehe auch Keplers Gesetze) 💫
Umgekehrt verrichtet der Komet Arbeit an der Sonne nachdem er sich wieder von der Sonne entfernt: Er verliert Energie und wird langsamer.
Wohin geht seine Energie? Die Sonne wird im Prozess ganz leicht beschleunigt. Da sie aber eine derart viel grössere Masse hat, ist die Beschleunigung vernachlässigbar.
Ein anderes Beispiel ist das Experiment des Fadenstrahlrohrs, das im Artikel zur Lorentzkraft genauer beschrieben wird.

Ein Strahl von Elektronen wird durch die Lorentzkraft umgelenkt, die genau senkrecht zur Geschwindigkeit der Elektronen gerichtet ist.
Weil der Winkel zwischen der Kraft und der Geschwindigkeit \(\alpha = 90^\circ\) beträgt, ist die Lorentzkraft nicht imstande, den Elektronen Energie zu geben oder von ihnen weg zu nehmen. Sie kann die Elektronen weder beschleunigen, noch kann sie sie abbremsen.
Die immer senkrecht wirkende Lorentzraft kann nur umlenken. Sie kann nicht beschleunigen oder abbremsen.
Arbeit als Fläche im Kraft-Weg-Diagramm (F,s-Diagramm)
Arbeit kann in einem Kraft-Weg-Diagramm (\(F,s\)-Diagramm) als Fläche dargestellt werden. Dies gilt bei allen Arten von Arbeit. Wir betrachten dazu dünne Flächenstücke mit der Höhe der Kraft:
\[ \Delta W_i=F_i \cdot \Delta s_i \]
Wenn wir nur eine sehr kleine Wegstrecke \(\Delta s\) zurücklegen, verändert sich die Kraft auch nur sehr geringfügig. Wir können deshalb näherungsweise annehmen, dass die Kraft \(F_i\) konstant ist und somit die Rechteckfläche nehmen.
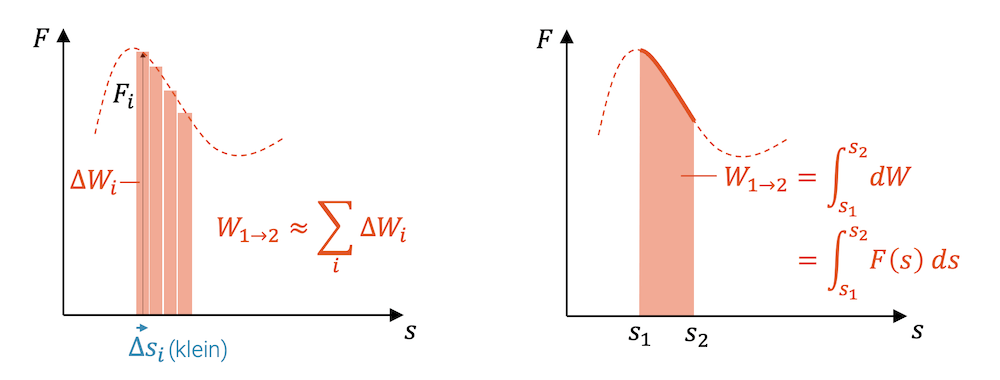
Diese Flächenstücke entsprechen kleinsten Mengen von Energie \(\Delta W_i\). Wenn wir sie alle summieren, kriegen wir die Arbeit, die durch die Kraft verrichtet wird:
\[ W \approx \sum_i \Delta W_i = \sum_i F_i \cdot \Delta s_i \]
Die Summe wird normalerweise als Integral geschrieben und die kurze Wegstrecke wird infinitesimal klein gemacht:
\[ \Delta s \rightarrow ds \]
\[ W = \int dW = \int_{s_1}^{s_2} F \cdot ds \]
Unter dem Verlauf der Kraft im Kraft-Weg-Diagramm entspricht die Fläche der geleisteten Arbeit \(W\). 👍
Weitere Videos
(keine externe Youtube-Videos zu diesem Thema)
Aufgabensammlung
Lernziele
Mini-Test
Um Zugang zum Mini-Test zu kriegen,
musst du vollwertiges Mitglied im Hacker-Club sein.
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt








Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.