Transformator

Transformatoren sind wichtige Geräte, die Wechselspannungen transformieren. Sie funktionieren nach dem Prinzip der Gegeninduktion. Eine angelegte Spannung \(U_1\) wird an die Primärspule des Transformators angelegt. Über das Windungsverhältnis \(\frac{N_2}{N_1}\) wird bestimmt, welche Spannung in der Sekundärspule induziert wird:

\[ \frac{U_2}{U_1} = -\frac{N_2}{N_1} \]

Wir können auch mit \(U_1\) multiplizieren und wie folgt schreiben:

\[ U_2 = – \frac{N_2}{N_1} \cdot U_1 \]

Für eine Wechselspannung mit der Kreisfrequenz \(\omega\) erhalten wir:

\[ U_2(t) = – \frac{N_2}{N_1} \cdot U_1 \cdot \sin(\omega t) \]

Die Spannung \(U_2\) ist wieder eine sinusförmige Wechselspannung mit einer Phasenverschiebung von 180° bzw. \(\pi\) (Bogenmass), was wir am Minuszeichen erkennen. Das Windungszahlenverhältnis \(\frac{N_2}{N_1}\) ist ein Vergrösserungs- oder Verkleinerungsfaktor mit welchem die Spannung \(U_1\) multipliziert wird.

Im weiteren schauen wir uns ein paar Beispiele von Transformatoren mit verschiedenen Windungsverhältnissen an. Die am Transformator angelegte Spannung beträgt jeweils:

\[ U_1(t) = 3\;\text{V} \cdot \sin(\omega t) \]

Beachte, dass der Kern es erlaubt, dass die beiden Spulen nicht in der gleichen Achse liegen, sondern einander gegenüber sind. Das ist in den meisten Fällen sehr praktisch, weil sehr grosse Windungszahlen entsprechenden Platz benötigen. Zudem wird mit dieser Anordnung verhindert, dass viel vom Magnetfeld nach aussen austritt. Beim Stabmagneten müssen die geschlossenen Magnetfedlinien ja alle irgendwie ihren Weg zurück zum anderen Pol finden. Hier sind sie im Kern und bleiben auch dort.

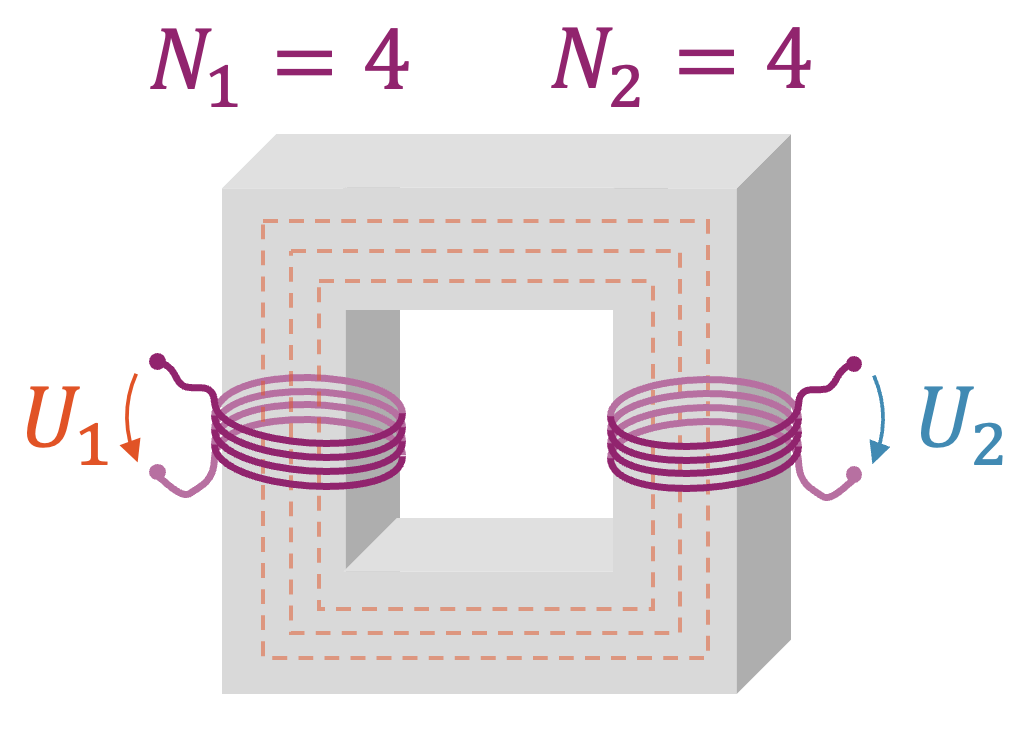
In obigen ersten Beispiel sind die Windungszahlen der Primär- und der Sekundärspulen gleich. Damit ist das Windungszahlenverhältnis \(\frac{N_2}{N_1}=1\) und die beiden Spannungen \(U_1\) und \(U_2\) sind bis auf das Vorzeichen gleich. Das Vorzeichen entspricht der 180°-, respektive der \(\pi\)-Phasenverschiebung in Bogenmass, denn es gilt:

\[ \sin(t) = -\sin(t+\pi) \]

Somit haben wir:

\[ U_2(t) = 3\;\text{V} \cdot \sin(\omega t + \pi) \]

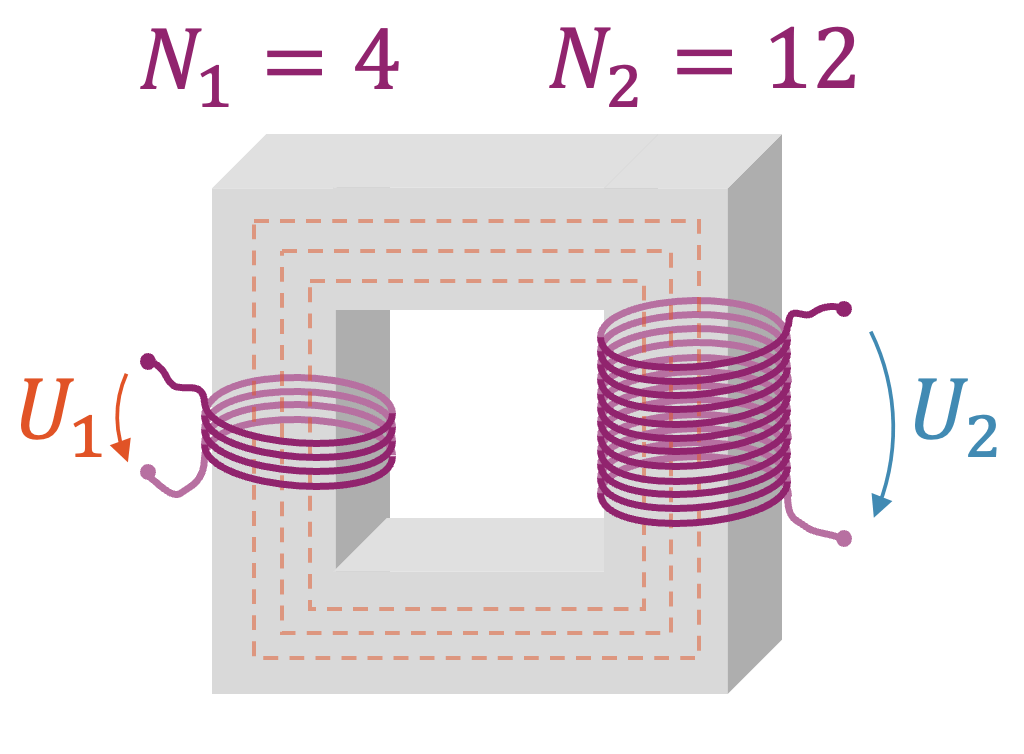
Im zweiten Beispiel haben wir in der Sekundärspule eine dreimal grössere Windungszahl \(N_2\) als in der Primärspule. Das Windungszahlenverhältnis ist demnach

\[ \frac{N_2}{N_1} = \frac{12}{4} = 3 \]

Damit folgt

\[ U_2(t) = -3 \cdot U_1(t) = 9\;\text{V} \cdot \sin(\omega t + \pi) \]

Man sagt auch, dass die Spannung \(U_1\) auf die dreimal grössere Spannung \(U_2\) hochtransformiert worden ist. Wir könnten uns natürlich ein noch grösseres Windungszahlenverhältnis vorstellen und damit noch grössere Spannungen erreichen. Auch könnten wir die Spannung \(U_2\) an die Primärspule eines zweiten Transformators anschliessen und damit eine nochmals vergrösserte Spannung \(U_3\) erzeugen.

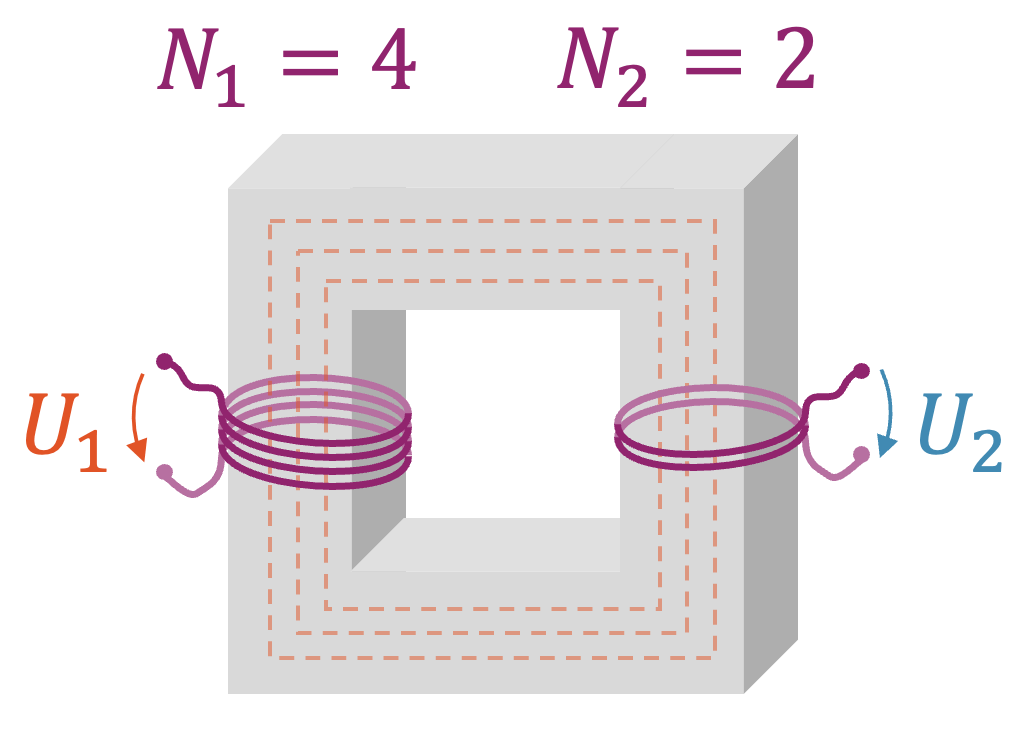
Im dritten Beispiel haben wir das folgende Windungszahlenverhältnis:

\[ \frac{N_2}{N_1}=\frac{1}{2} \]

Hier wird eine angelegte Spannung \(U_1\) heruntertransformiert auf eine halb so grosse Spannung \(U_2\). Auf diese Art und Weise können hohe Spannungen wieder herunter geholt werden.

\[ U_2 = 1.5\;\text{V} \cdot \sin(\omega t + \pi) \]