Videos

Image by Siemens, licensed under CC BY-SA 3.0
Der Generator ist ein umgekehrter Elektromotor. Statt dass elektrische Arbeit in mechanische Arbeit umgewandelt wird, geht es in die umgekehrte Richtung. Eine mechanische Arbeit wird in elektrische Arbeit umgewandelt. Wir sprechen von elektrischer Arbeit, weil sie sofort wieder anderswo ”verbraucht” wird. Sie wird z.B. umgewandelt durch einen elektrischen Motor.
Wir können die Umkehrung auch am einfachen Leiter erkennen. Wenn wir durch einen Leiter einen elektrischen Strom schicken und dieser Leiter durch ein Magnetfeld führt, stellt sich eine Lorentzkraft auf die Ladungsträger und somit auf den Leiter ein. Wir wenden die Rechte-Hand-Regel an: Der Daumen zeigt nach unten. Das Magnetfeld zeigt in die Zeichenebene hinein. In diese Richtung setzen wir den Zeigefinger. Die restlichen Finger geben uns die Richtung nach rechts für die Lorentzkraft.
Wäre dieser einfache Leiter beweglich, würde er sich jetzt nach rechts bewegen, d.h. aus elektrischer Arbeit würde mechanische Arbeit gemacht. Wir haben hier das Grundprinzip eines Elektromotors.
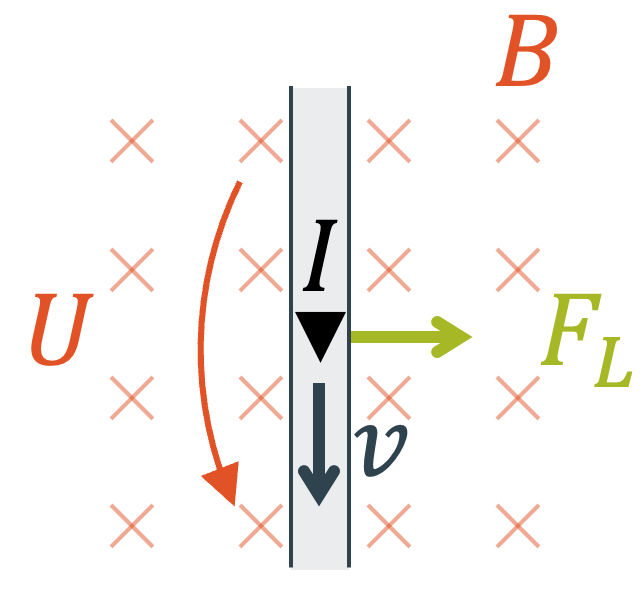
Wir nehmen den gleichen (beweglichen) Leiter. Dieses Mal wird aber kein Strom durch ihn geschickt, sondern wir bewegen diesen Leiter mechanisch durch das Magnetfeld. Die Lorentzkraft wirkt wieder, aber dieses Mal zeigt sie nach oben, d.h. die positiven Ladungen werden nach oben gedrückt, die negativen Ladungen drückt es nach unten. Diese Ladungstrennung lässt die elektrische Spannung \(U_{ind}\) entstehen, die z.B. einen elektrischen Verbraucher antreiben könnte.
Hier haben wir das Grundprinzip des Generators: Er wandelt mechanische Arbeit in elektrische Arbeit um.
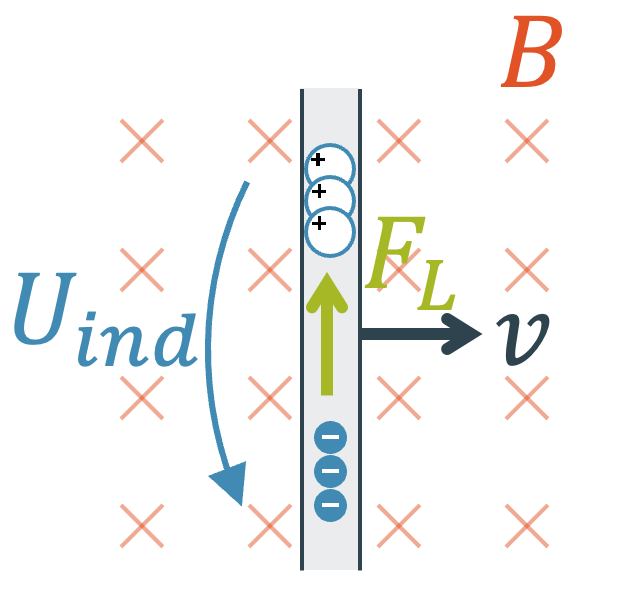
Grundprinzip des Generators: Mechanische Arbeit wird zu elektrischer Arbeit umgewandelt.
In Generatoren werden nicht gerade Leiter seitwärts bewegt, sondern Leiterschlaufen werden im Magnetfeld gedreht. Der Vorteil liegt darin, dass die Drehbewegung unbeschränkt wiederholt werden kann. Zudem bewirkt das dauernde neue Ausrichten der Leiterschlaufe im Magnetfeld ein andauerndes Ändern des magnetischen Flusses, so dass ebenfalls dauernd eine elektrische Spannung induziert wird. Wenn statt einer Leiterschlaufe eine ganze Spule mit \(N\) Windungen im Magnetfeld gedreht wird, ist die induzierte Spannung \(N\)-fach grösser, was auch wieder ein Vorteil ist.
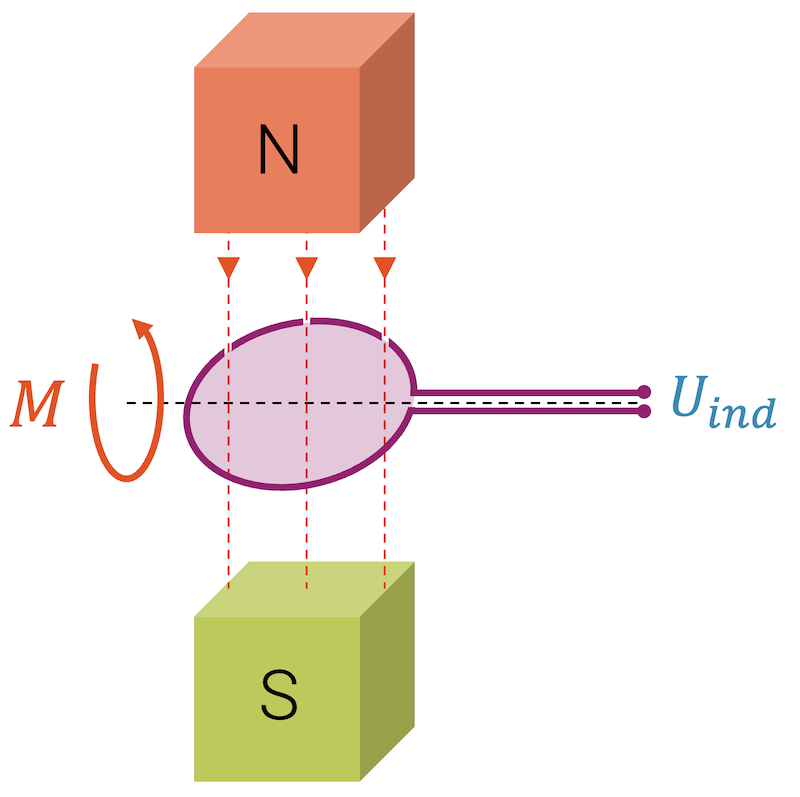
Die durch das äussere Drehmoment erzwungene Drehbewegung verändert den magnetischen Fluss in der Schlaufe (Spule) und induziert damit die Spannung \(U_{ind}\).
Der Generator ist die Umkehrung des elektrischen Motors, indem er mechanische Arbeit in elektrische Arbeit umwandelt.
Elektrische Motoren können auch als Generatoren verwendet werden: z.B. Rekuperation der kinetischen Energie beim Bremsen (Tram)
Entstehung der sinus-förmigen Wechselspannung
In der nachfolgenden Grafik sehen wir die Fläche der Leiterschlaufe von der Seite, wie sie mit der Zeit im konstanten Magnetfeld gedreht wird. Wenn sie die gleiche Richtung hat, wie das Magnetfeld, dann haben wir keinen magnetischen Fluss \(\Phi_B\). Wenn Sie hingegen senkrecht zum Magnetfeld steht, ist der magnetische Fluss \(\Phi_B\) maximal.
Der magnetische Fluss \(\Phi_B(t)\) nimmt die Form einer Sinus-Funktion mit der Winkelgeschwindigkeit \(\omega\) ein. Zur Vereinfachung ignorieren wir die Amplitude und setzen sie einfach 1:
\[ \Phi_B(t) = \sin(\omega t) \]
Mit dem Induktionsgesetz erhalten wir die induzierte Spannung \(U_{ind}\):
\[ U_{ind}(t) = – N \cdot \frac{d}{dt} \Phi_B(t) \]
\[ U_{ind}(t) = – N \cdot \frac{d}{dt} \sin (\omega t) \]
\[ = – N \omega \cdot \cos(\omega t) \]
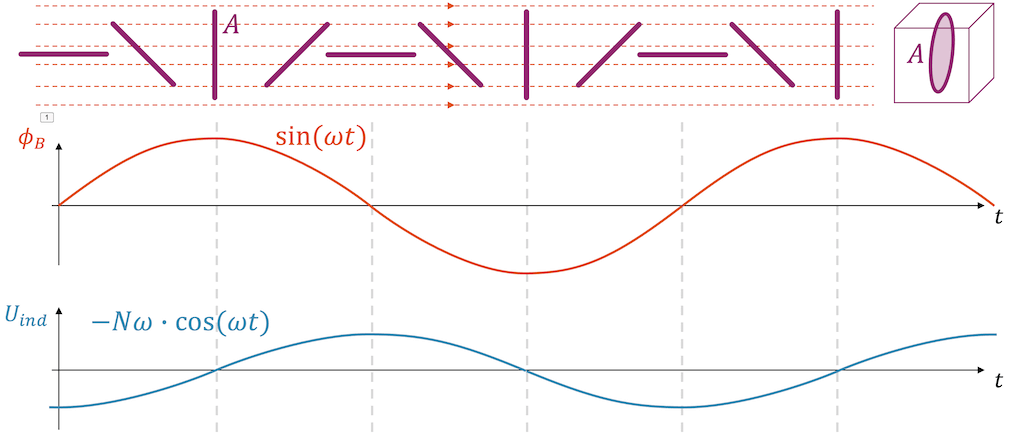
Wir erhalten eine Kosinusfunktion mit der gleichen Winkelgeschwindigkeit \(\omega\), d.h mit der gleichen Frequenz wie die Drehung der Leiterschlaufe. Ob Kosinus oder Sinus ist eigentlich egal, da beide Funktionen gleich sind, bis auf eine Phasenverschiebung. Wir haben eine kosinus- bzw. eine sinusförmige Wechselspannung erhalten.
Tatsächlich hat die Spannung an der Steckdose einen sinusförmigen Verlauf. Es ist eine Wechselspannung, weil sie, wie eben beschrieben, durch eine rotierende Leiterschlaufe entstanden ist. Dabei ist die Spannung von 230 V nicht die Amplitude der Sinusfunktion. Sie beträgt 325 V.
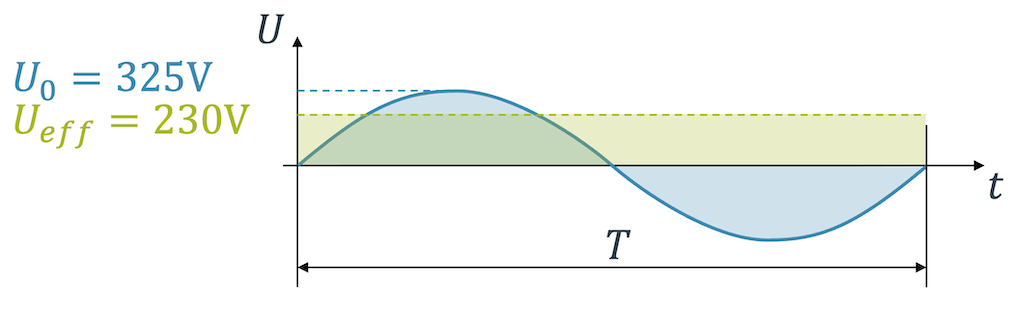
Die 230 V sind das quadratische Mittel der Spannung. Tatsächlich schwankt die Spannung ja zwischen +325V und -325V. Zwischendurch ist sie immer wieder auch 0 V. Im Mittel ist sie aber 230 V. Diese Spannung wird effektive Wechselspannung \(U_{eff}\) bezeichnet.
Die meisten Generatoren im westeuropäischen Stromnetz drehen mit 3000 Umdrehungen pro Minute. Das entspricht einer Frequenz von \(f=50\;\text{Hz}\) :
\[ f = \frac{3000}{1\;\mathrm{min}} = \frac{3000}{65\;\mathrm{s}} \]
\[ = \frac{50}{\mathrm{s}} = 50\;\text{Hz} \]
Durch die Drehbewegung entspricht der magnetische Fluss in der Schlaufe (Spule) einer Sinusfunktion. Die zeitliche Änderung dieser Funktion führt wieder zu einer Sinusfunktion für die induzierte Spannung, jedoch mit Phasenverschiebung. Ein Generator produziert deshalb eine sinusförmige Wechselspannung mit der gleichen Frequenz, wie die Kreisbewegung der Leiterschlaufe.
Die Kraftwerke im westeuropäischen Netz erzeugen alle eine synchrone Wechselspannung mit der gleichen Frequenz von 50 Hz.
Die Nennspannung von 230 V entspricht der effektiven Spannung \(U_{eff}\), die das quadratische Mittel der Wechselspannung ist. Die Amplitude der Wechselspannung ist mit rund 325 V deutlich grösser.
Aufgabensammlung
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.





Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.