Stromkreis/Schaltplan

Wir wissen, dass wir mit einem äusseren elektrischen Feld die freien Ladungsträger (Elektronen) im Metall der Leiter zum Fliessen bringen können. Wenn wir eine Batterie nehmen, haben wir zwischen den Polen eine elektrische Spannung bzw. Potenzialdifferenz:

\[ U = \varphi_A – \varphi_B \]

Aus der Beziehung \(U = E_0 d\) folgt \(E_0 = \frac{U}{d}\). Wir wissen jetzt nicht, welchen Abstand wir für \(d\) einsetzen müssten, aber wir erkennen, dass wir mit Hilfe der zwei Pole und ihrer elektrischen Spannung ein elektrisches Feld erzeugen können, das die Ladungen antreibt.

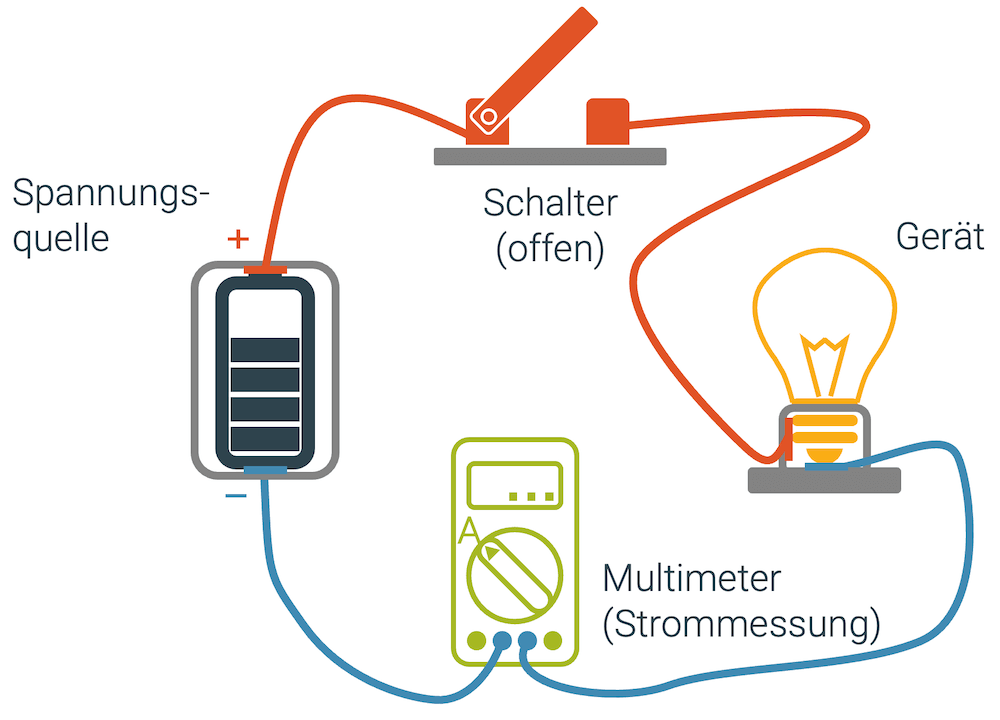
Genau das macht man in einem Stromkreis. Hier ist ein solcher einfacher Stromkreis gezeigt. Eine Batterie ist über einen Leiter an einen Schalter angeschlossen. Der Schalter ist offen, d.h. er macht noch keinen Kontakt und lässt die Ladungsträger noch nicht fliessen. Der Leiter führt weiter zu einer kleinen Lampe. Nach der Lampe führt ein Leiter zu einem Strommessgerät und schliesslich führt ein Leiter wieder zurück an die Batterie, dieses Mal aber an den anderen Pol.

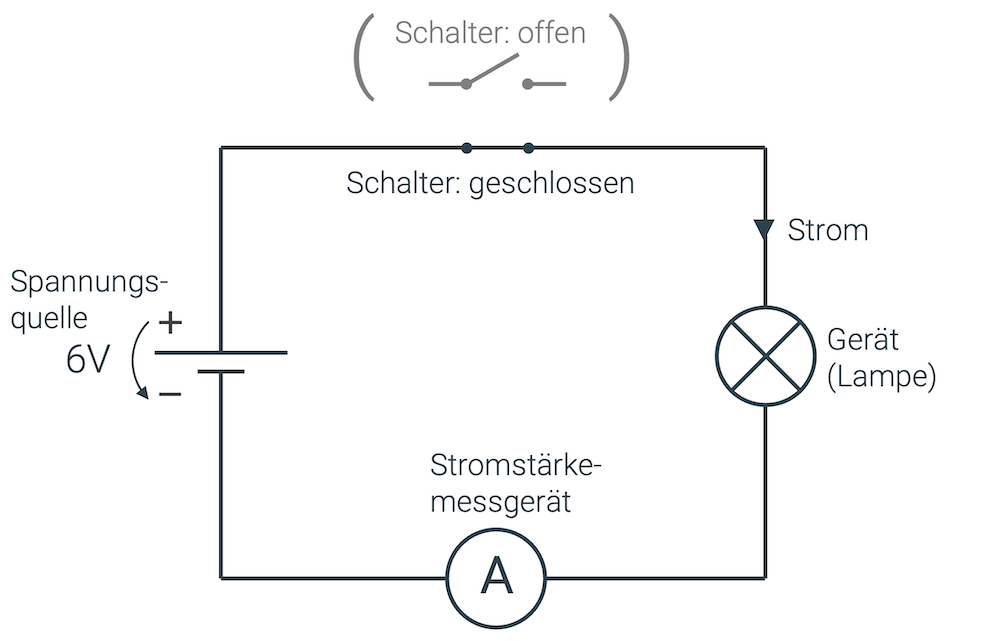
In der Skizze rechts ist ein sog. Schaltplan gezeichnet. Er zeigt das Gleiche wie die linke Skizze, ist jedoch minimalistisch gehalten, so dass wir auf einen Blick die Übersicht über den Stromkreis und seine Komponenten erhalten.

Wenn der Schalter und damit auch der Stromkreis geschlossen sind, können die Ladungen in diesem Stromkreis fliessen, ohne dass sie sich irgendwo anhäufen können. Wie gesagt: Eine Anhäufung der Ladungen wird nicht stattfinden, da sie sich gegenseitig abstossen und deshalb immer ideal verteilt bleiben. Einzige Ausnahme hier ist der Kondensator auf dessen Platten eine Anhäufung stattfindet, die aber mit der Anziehung zur anderen Platte begründet werden kann.

Wird der Stromkreis irgendwo unterbrochen, so spricht man von einem offenen Stromkreis. Es kann nichts fliessen, weder vor dem Unterbruch, noch hinter dem Unterbruch, denn das würde immer zu einer Anhäufung von Ladung von der einen oder der anderen Art führen. Ein einseitiges Abfliessen von negativer Ladung wäre ja eine Anhäufung von positiven Löchern.

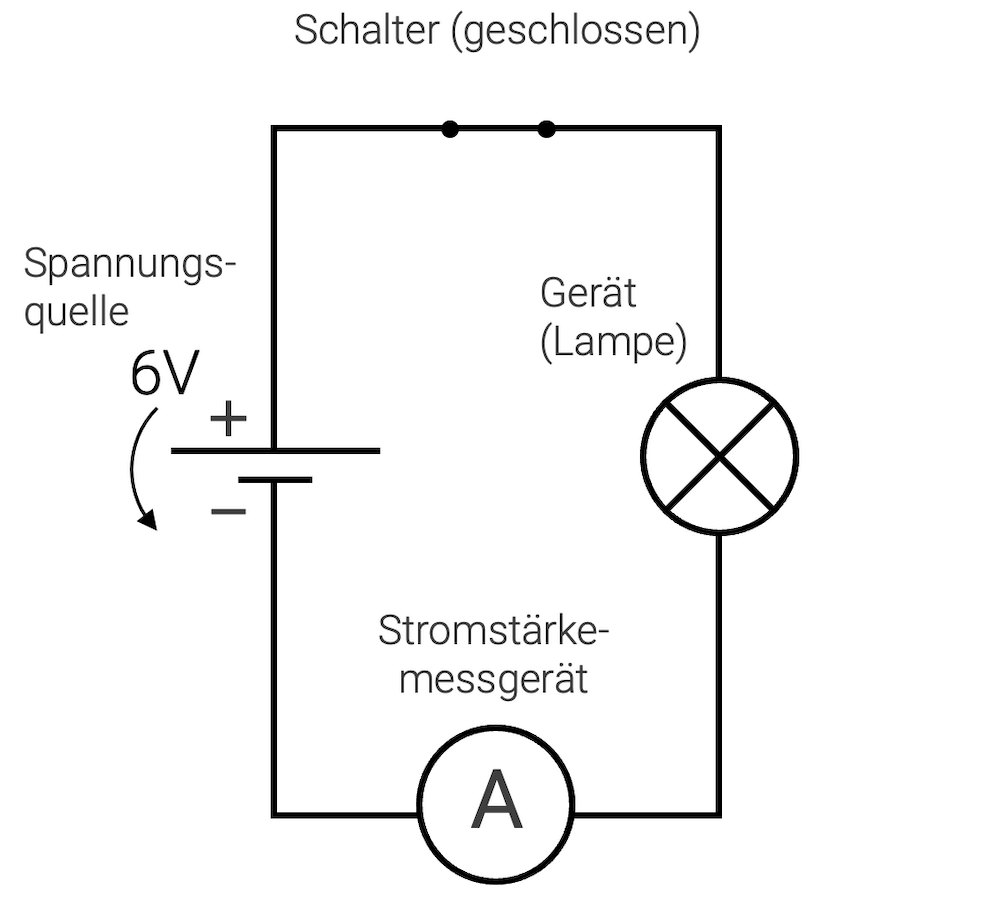
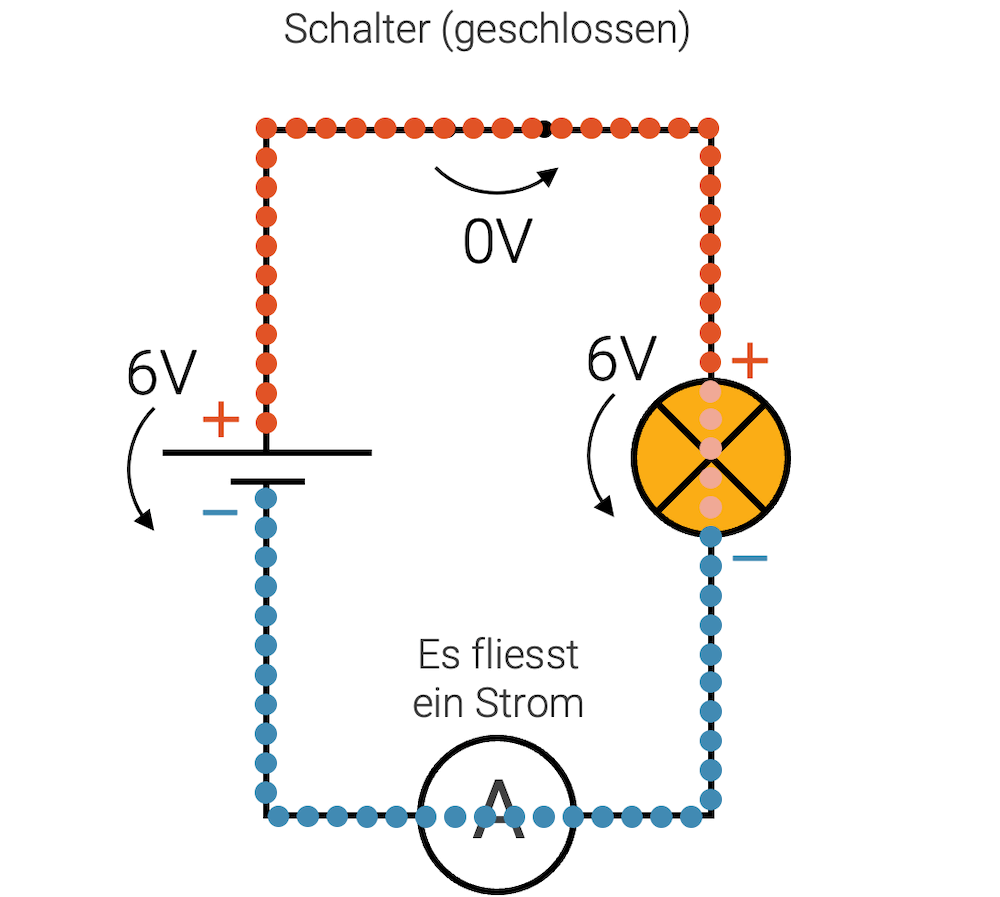
Zuerst schauen wir uns die Situation mit geschlossenem Schalter an: Die Ladungen im Leiter sind vom Pluspol der Batterie über den Schalter bis hin zum oberen Anschluss der Lampe auf dem Potenzial \(\varphi_A = +6\,\text{V}\) (rot). Starten wir vom Minuspol der Batterie aus, so sind alle Ladungsträger bis zum unteren Anschluss der Lampe auf dem Potenzial \(\varphi_B = 0\,\text{V}\) (blau).

An der Batterie zeichnen wir einen Pfeil vom hohen zum niederen Potenzial und schreiben die Potenzialdifferenz bzw. Spannung in Volt hin. An der Batterie haben wir \(6\,\text{V}\) Spannung. Da die beiden Potenziale \(\varphi_A\) und \(\varphi_B\) sich bis zu den beiden Anschlüssen der Lampe erstrecken, haben wir auch an der Lampe eine Spannung von \(6\,\text{V}\). Man sagt hier auch, dass über der Lampe eine Spannung von \(6\,\text{V}\) liegt. Für die Ladungen in der Lampe bedeutet das, dass sie ein treibendes elektrisches Feld haben. Der Strom fliesst im ganzen Stromkreis und die Lampe leuchtet.

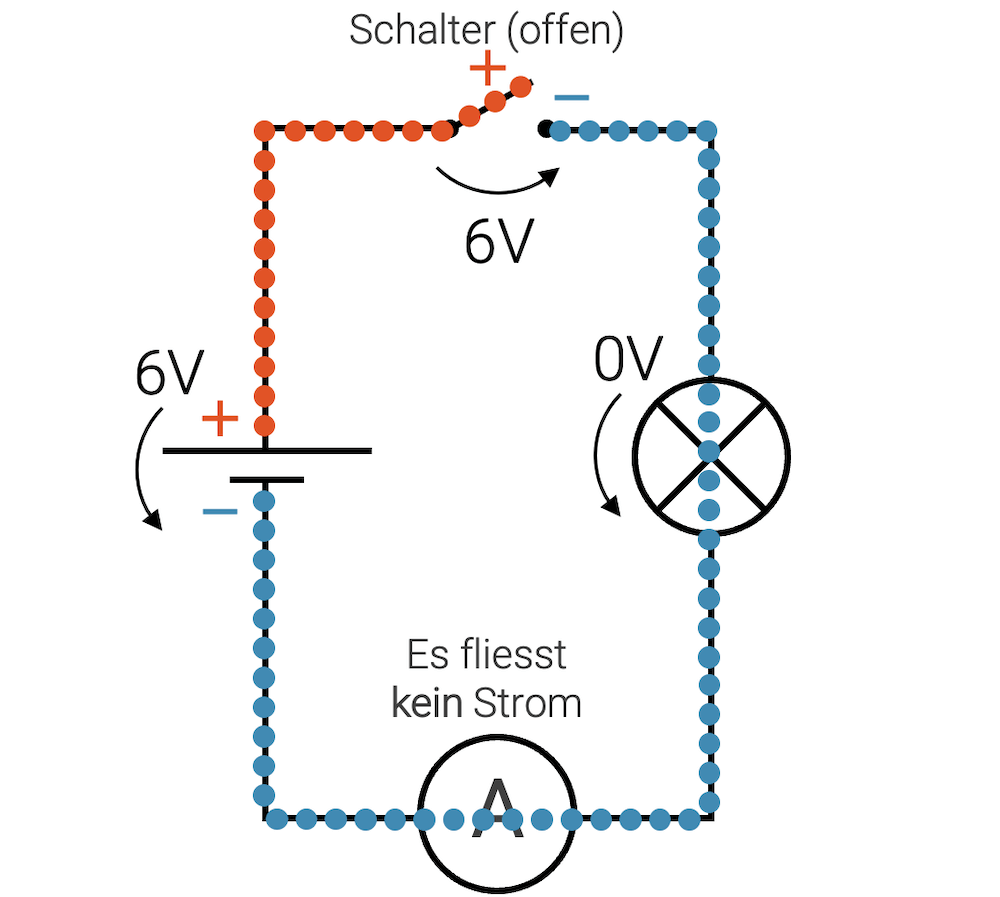
Im Fall des offenen Schalters kann das Potenzial \(\varphi_A\) von \(+6\,\text{V}\) nur bis zum linken Ende des Schalters gelangen (rot). Das Potenzial \(\varphi_B\) bei \(0\,\text{V}\) erstreckt sich jetzt vom Minuspol der Batterie bis zum rechten Ende des Schalters (blau). Über der Lampe haben wir keine Spannung mehr, d.h. es gibt dort keinen Antrieb für elektrischen Strom mehr. Die Spannung liegt jetzt über dem Schalter, doch da kann nichts fliessen. Im ganzen Stromkreis fliesst kein Strom und die Lampe bleibt dunkel.

Beispiel

In der folgenden Schaltung sind vier gleiche Lampen verbaut.

Was passiert, wenn wir den Schalter A öffnen?

Was passiert, wenn beide Schalter geschlossen sind?

Welche Lampe leuchtet am hellsten? Welche leuchtet nicht?

---

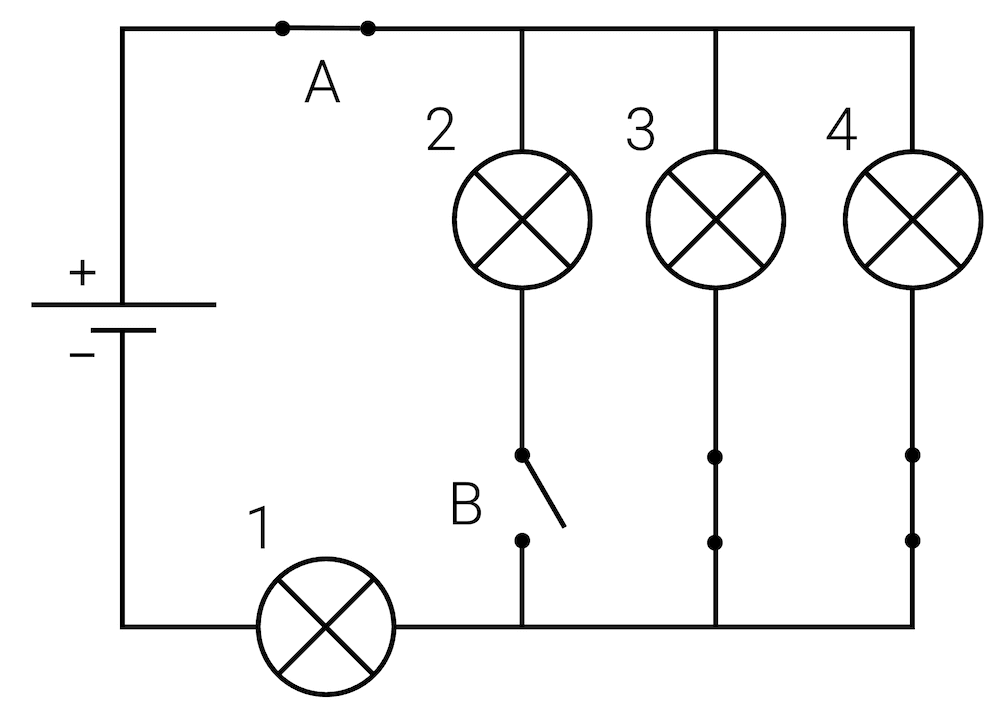
Eines vorweg: Wenn wir den Schalter A öffnen, unterbrechen wir den ganzen Stromkreis und nichts kann mehr fliessen. Alle Lampen würden dann ausgehen.

Jetzt schauen wir uns die Potenziale an: Wir sehen, dass das Potenzial \(\varphi_A\) vom Pluspol der Batterie bis zum Schalter B reicht, aber nicht weiter. Dann führen die Leiter das Potenzial \(\varphi_A\) auch zu den oberen Anschlüssen der Lampen 3 und 4 (rot). Das Potenzial des Minuspols \(\varphi_B\) geht zum linken Anschluss der Lampe 1. Zwischen den Lampen 1, 3 und 4 haben wir ein Zwischenpotenzial, irgendwo zwischen \(+6\,\text{V}\) (rot) und \(0\,\text{V}\) (blau). Wir haben diese “halbe Höhe” deshalb schwach rot eingefärbt.

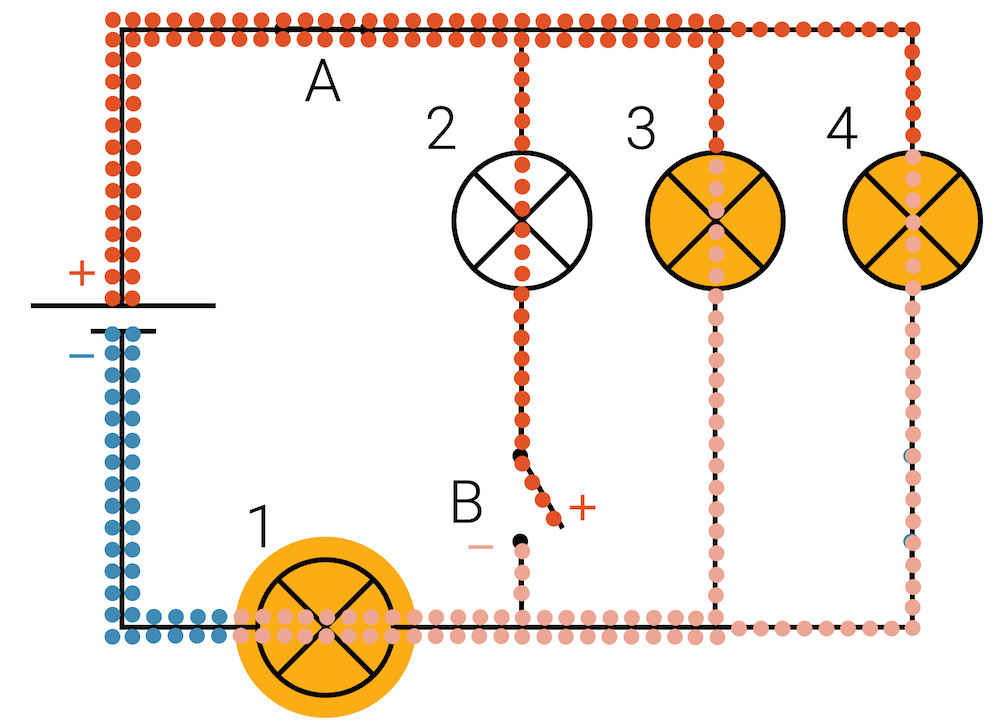
Da über der Lampe 2 keine Spannung anliegt, ist sie dunkel. Der Leiter ist auch eine Sackgasse und in einer Sackgasse kann keine Ladung fliessen, ohne dass sie sich anhäufen würde, was ja nicht geht. Lampe 2 ist definitiv aus.

Über den Lampen 3 und 4 haben wir eine unbekannte Spannung, die sicher weniger als \(6\,\text{V}\) beträgt. Wenn wir annehmen, dass das Zwischenpotenzial auf der Höhe von \(+4\,\text{V}\) steht, dann haben die Lampen 3 und 4 eine Spannung von \(2\,\text{V}\) (von \(+6\,\text{V}\) auf \(+4\,\text{V}\) runter). Beide Lampen leuchten.

Die Lampe 1 hätte unter der gleichen Annahme eine Spannung von \(4\,\text{V}\) (von \(+4\,\text{V}\) auf \(0\,\text{V}\) runter). Auch sie leuchtet. Sie leuchtet sogar heller, da doppelt so viele Ladungen durch sie durchfliessen als durch 3 und 4.

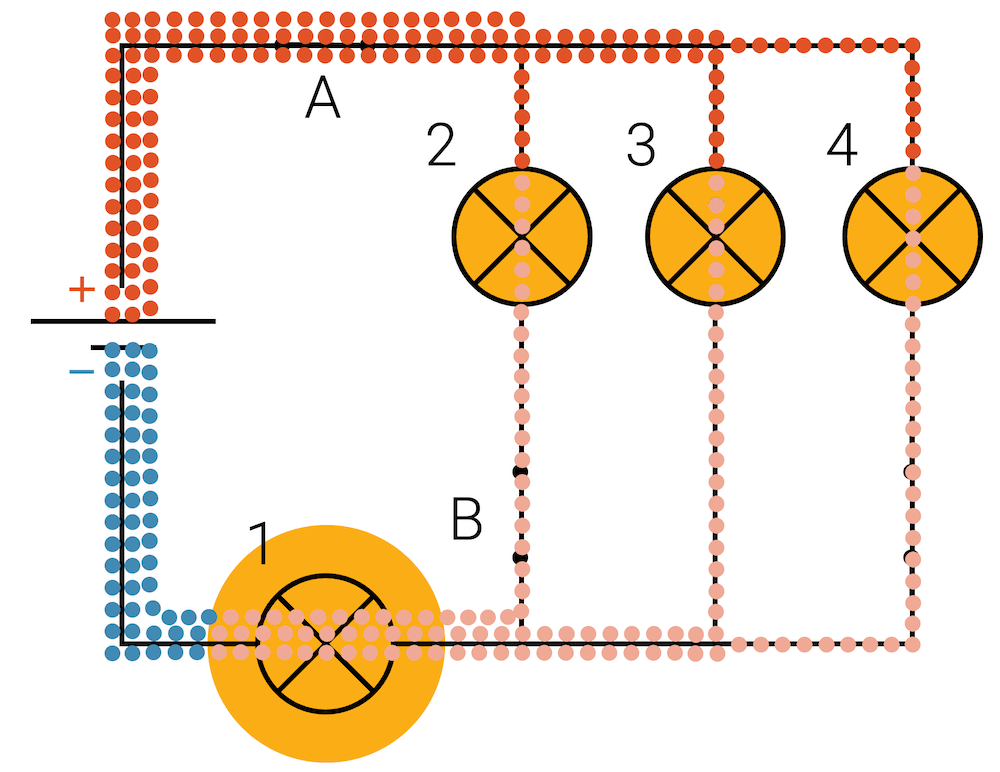
Jetzt schliessen wir den Schalter B. Dadurch kann sich das Zwischenpotenzial bis zum unteren Anschluss der Lampe 2 ausbreiten und die Lampe 2 steht damit unter Spannung. Alle drei Lampen 2, 3 und 4 sind jetzt gleich gestellt. Sie haben alle die gleiche Spannung und leuchten deshalb gleich stark. Die Lampe 1 wird am hellsten leuchten, da am meisten Ladung durch sie durchfliesst.