Inhalt
Das Wichtigste in Kürze
Die Summe zweier Vektoren \(\vec{a}\) und \(\vec{b}\) ergibt selber wieder einen Vektor. Der Summenvektor wird gebildet, indem die einzelnen Komponenten addiert werden.
\[ \begin{pmatrix} a_x \\ a_y \end{pmatrix} + \begin{pmatrix} b_x \\ b_y \end{pmatrix} = \begin{pmatrix} a_x+b_x \\ a_y+b_y \end{pmatrix} \]
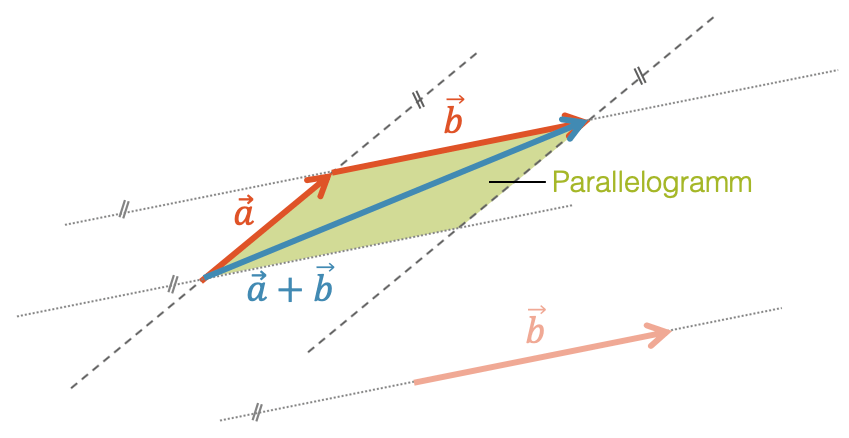
Die beiden Vektoren \(\vec{a}\) und \(\vec{b}\) bilden ein Parallelogramm. Der Summenvektor \((\vec{a} + \vec{b})\) ist die Diagonale des Parallelogramms.
Videos
Vektoren addieren
Wir schauen uns ein Beispiel an und addieren die beiden Vektoren \(\vec{a} = \begin{pmatrix} 1 \\ 2 \end{pmatrix}\) und \(\vec{b} = \begin{pmatrix} -3 \\ 1 \end{pmatrix}\). Wir addieren dabei die Koeffizienten der gleichen Dimension und erhalten so einen neuen Vektor:
\[ \vec{a} + \vec{b} = \begin{pmatrix} 1 \\ 2 \end{pmatrix} + \begin{pmatrix} -3 \\ 1 \end{pmatrix} \]
\[ = \begin{pmatrix} 1+(-3) \\ 2+1 \end{pmatrix} = \begin{pmatrix} -2 \\ 3 \end{pmatrix} \]
Es wird sofort klar, dass wir auch in der anderen Reihenfolge addieren können und dabei das gleiche Resultat erhalten:
\[ \vec{b} + \vec{a} = \begin{pmatrix} -3 \\ 1 \end{pmatrix} + \begin{pmatrix} 1 \\ 2 \end{pmatrix} \]
\[ = \begin{pmatrix} (-3)+1 \\ 1+2 \end{pmatrix} = \begin{pmatrix} -2 \\ 3 \end{pmatrix} \]
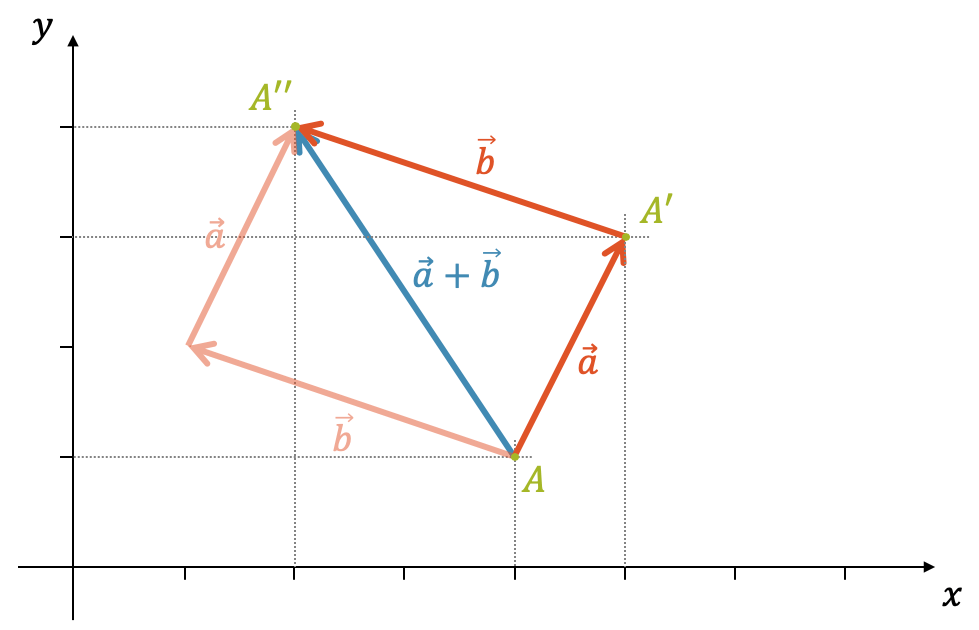
Nun schauen wir uns die Addition im zweidimensionalen Koordinatensystem an. Der erste Vektor \(\vec{a}\) bildet \(A\) auf \(A’\) ab, der zweite Vektor \(b\) bildet \(A’\) auf \(A”\) ab. Die Summe der beiden Vektoren \((\vec{a}+\vec{b})\) ist somit eine Abbildung von \(A\) direkt auf \(A”\).
Wir sehen, dass die umgekehrte Reihenfolge der Addition zum gleichen Resultat führen:
\[ (\vec{a}+\vec{b}) = (\vec{b}+\vec{a}) = \overrightarrow{AA”} \]
\[ = \begin{pmatrix} -2 \\ 3 \end{pmatrix} \]
Die Summe zweier Vektoren \(\vec{a}\) und \(\vec{b}\) ergibt selber wieder einen Vektor. Der Summenvektor wird gebildet, indem die einzelnen Komponenten addiert werden.
\[ \begin{pmatrix} a_x \\ a_y \end{pmatrix} + \begin{pmatrix} b_x \\ b_y \end{pmatrix} = \begin{pmatrix} a_x+b_x \\ a_y+b_y \end{pmatrix} \]
Die beiden Vektoren \(\vec{a}\) und \(\vec{b}\) bilden ein Parallelogramm. Der Summenvektor \((\vec{a} + \vec{b})\) ist die Diagonale des Parallelogramms.
Beispiel
Gegeben sind die beiden Vektoren \(\vec{a}\) und \(\vec{b}\). Addiere die beiden Vektoren grafisch.
Wir bilden das Parallelogramm, indem wir z.B. den Vektor \(\vec{b}\) parallel verschieben, so dass je eine Linie von \(\vec{b}\) durch den Anfang und das Ende von \(\vec{a}\) verläuft. Dann ziehen wir die Parallele zu \(\vec{a}\) und erhalten so das Parallelogramm.
Sobald wir das Parallelogramm haben, können wir die Diagonale zeichnen. Sie ist die Summe \((\vec{a} + \vec{b})\).
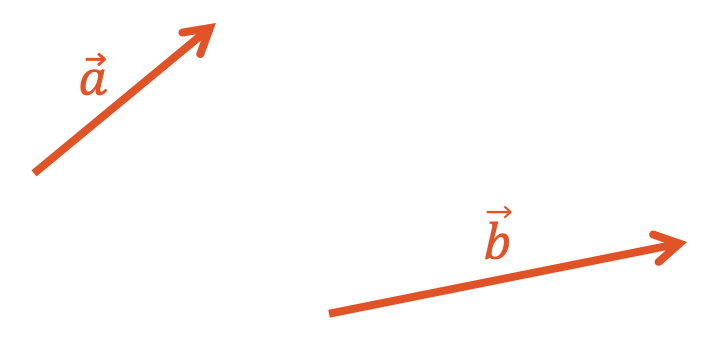
Vektoren subtrahieren
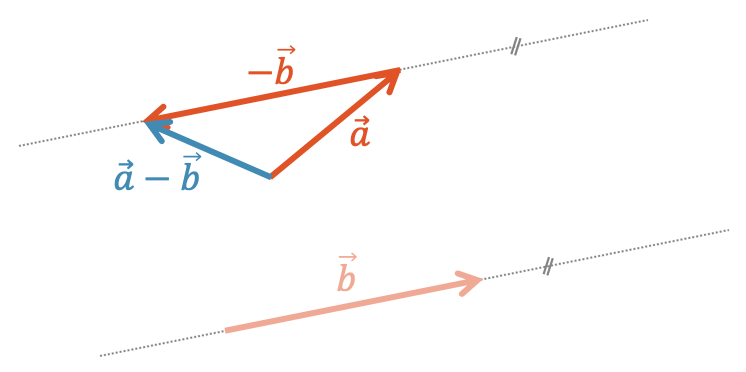
Wenn wir z.B. den Vektor \(\vec{b}\) vom Vektor \(\vec{a}\) subtrahieren müssen, benutzen wir den Gegenvektor von \(\vec{b}\). So können wir jederzeit aus einer Subtraktion wieder eine Addition von zwei Vektoren machen, die wir ja kennen.
Für die Subtraktion von zwei Vektoren \(\vec{a}-\vec{b}\) brauchen wir den Gegenvektor von \(\vec{b}\): \((-\vec{b})\)
Wir addieren \(\vec{a}\) mit dem Gegenvektor von \(\vec{b}\):
\[ \vec{a} – \vec{b} \quad = \quad \vec{a} + (-\vec{b}) \]
Beispiel
Subtrahiere den Vektor \(\vec{b}\) vom \(\vec{a}\) mit der grafischen Methode.
Wir ziehen wieder die Parallele von \(\vec{b}\) durch den Endpunkt von \(\vec{a}\) und zeichnen nun den Gegenvektor zu \(\vec{b}\). So kriegen wir die grafische Summe \(\vec{a} + (-\vec{b}) = \vec{a} – \vec{b}\).
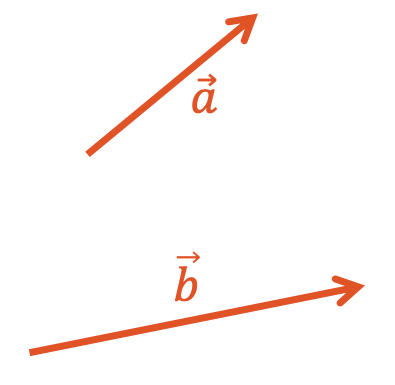
Beispiel
Berechne die Differenz \((\vec{a}-\vec{b})\) und stelle sie grafisch dar.
\[ \vec{a} = \begin{pmatrix} 2 \\ 0 \end{pmatrix}, \quad \vec{b} = \begin{pmatrix} 0 \\ -1 \end{pmatrix} \]
Wir schreiben die Differenz als Summe von \(\vec{a}\) und Gegenvektor \(-\vec{b}\) und addieren die Vektorkomponenten:
\[ (\vec{a} – \vec{b}) = \vec{a} + (-\vec{b}) \]
\[ = \begin{pmatrix} 2 \\ 0 \end{pmatrix} + \begin{pmatrix} 0 \\ -(-1) \end{pmatrix} = \underline{\begin{pmatrix} 2 \\ 1 \end{pmatrix}} \]
Aufgabensammlung
Mini-Test
Um Zugang zum Mini-Test zu kriegen,
musst du vollwertiges Mitglied im Hacker-Club sein.
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt
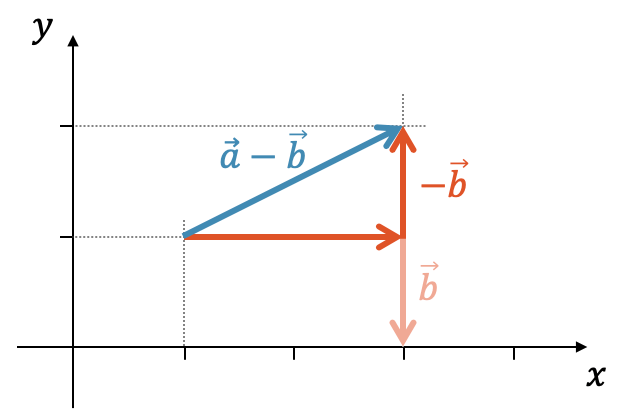
Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.