Inhalt
Videos
Nehmen wir einen Vektor und addieren ihn dreimal, so entsteht das Dreifache des Vektors:
\[ \vec{a}+\vec{a}+\vec{a} = 3 \cdot \vec{a} \]
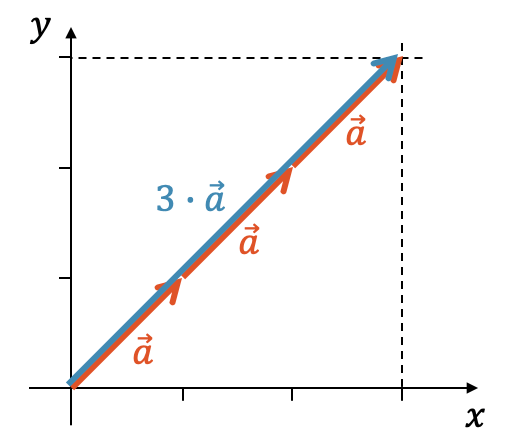
Die Richtung des Vektors \(\vec{a}\) wird beibehalten. Die Länge wird verdreifacht.
\[ \vec{a}+\vec{a}+\vec{a} = \begin{pmatrix}a_x \\ a_y \end{pmatrix} + \begin{pmatrix}a_x \\ a_y \end{pmatrix} + \begin{pmatrix}a_x \\ a_y \end{pmatrix} \]
\[ = \begin{pmatrix}a_x+a_x+a_x \\ a_y+a_y+a_y \end{pmatrix} = \begin{pmatrix} 3 \cdot a_x \\ 3 \cdot a_y \end{pmatrix} \]
\[ 3 \cdot \vec{a} = \begin{pmatrix} 3 \cdot a_x \\ 3 \cdot a_y \end{pmatrix} \]
Wir können das jetzt auch verallgemeinern mit dem Faktor \(k\):
\[ k \cdot \vec{a} = \begin{pmatrix} k \cdot a_x \\ k \cdot a_y \end{pmatrix} \]
Wird ein Vektor \(\vec{v}\) mit einer Zahl (Skalar) multipliziert, so multipliziert sich jede Komponente des Vektors mit dieser Zahl.
\[ k \cdot \vec{v} = \begin{pmatrix} k \cdot v_x \\ k \cdot v_y \end{pmatrix} \]
Der Vektor wird \(k\)-fach verlängert. Ist der Betrag von \(k\) kleiner eins, so wird der Vektor entsprechend verkürzt. Ein negatives \(k\) kehrt die Richtung des Vektors um.
Beispiel
Berechne den Vektor \(\vec{w}\), der die gleiche Richtung hat wie \(\;\vec{v} = \begin{pmatrix} 3 \\ -4 \end{pmatrix}\;\), aber die Länge 10 hat.
Mini-Test
Um Zugang zum Mini-Test zu kriegen,
musst du vollwertiges Mitglied im Hacker-Club sein.
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt







Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.