Inhalt
Das Wichtigste in Kürze
Die drei Vektoren \(\vec{a}\), \(\vec{b}\) und \(\vec{c}\) heissen komplanar, wenn wir die drei Vektoren in eine gemeinsame Ebene verschieben können.
Videos
Die drei Vektoren \(\vec{a}\), \(\vec{b}\) und \(\vec{c}\) heissen komplanar, wenn wir die drei Vektoren in eine gemeinsame Ebene verschieben können.
Warum reden wir hier von drei Vektoren? Ganz einfach: Zwei Vektoren sind immer komplanar. Wir könnten deshalb keine Bedingung aufstellen. Bei drei Vektoren ist das anders. Zwei Vektoren spannen eine gemeinsame Ebene auf. Es ist aber nicht unbedingt so, dass ein dritter Vektor automatisch in der gleichen Ebene liegt. Nur ein komplanarer Vektor tut das. Die Bezeichnung komplanar besteht aus den Teilen kom(mit) und planar (eben). Ein komplanarer Vektor ist mit den anderen beiden Vektoren in der gleichen Ebene.
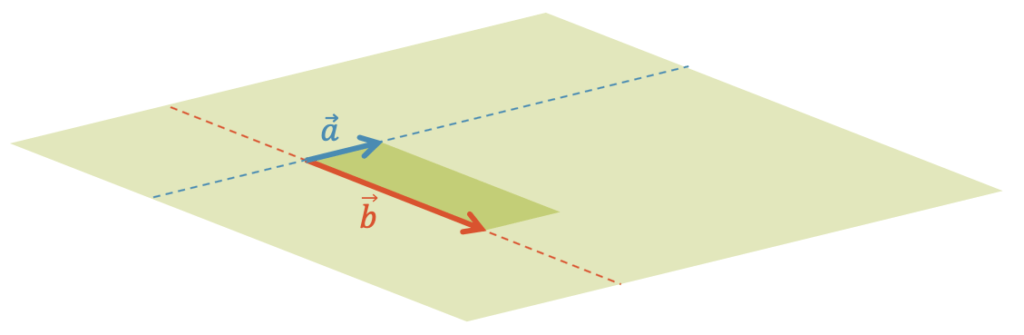
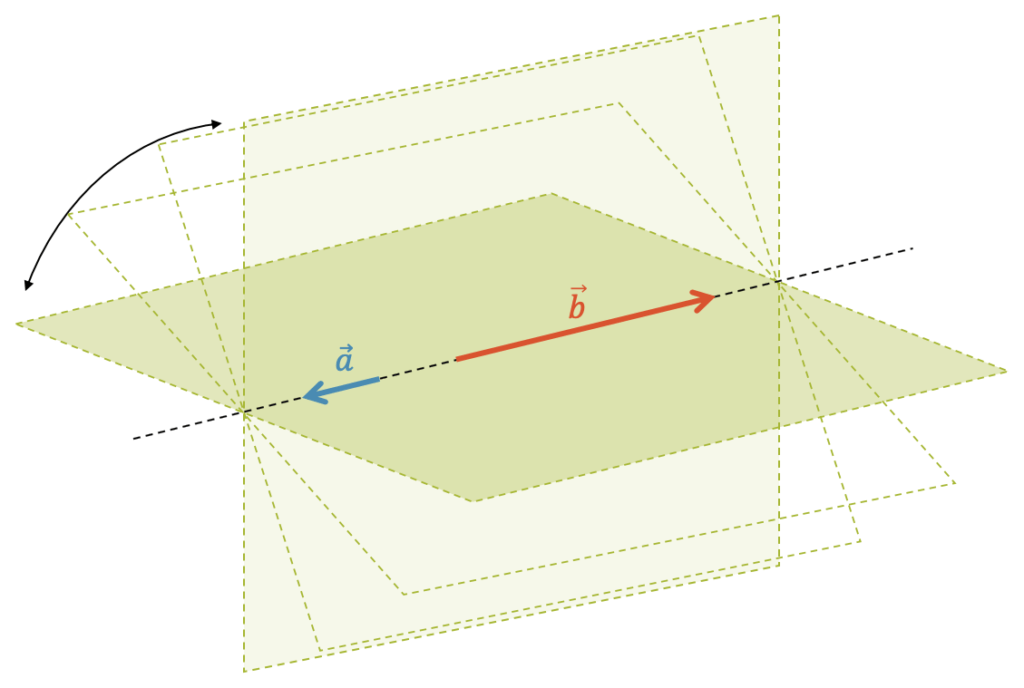
Können zwei Vektoren mehr als nur eine Ebene aufspannen? Ja, zwei kollineare Vektoren liegen auf einer gemeinsamen Gerade. Sie können keine Ebene aufspannen. Allerdings sind sie Bestandteil von von unendlich vielen Ebenen, nämlich all jenen, die die Gerade beinhalten und beliebig rotiert sind.
Beispiel
Erkläre, warum der Einheitsvektor in \(x\)-Richtung \(\vec{e}_x\), der Einheitsvektor in \(y\)-Richtung \(\vec{e}_y\) und der Vektor \(\vec{a}=\vec{e}_x + \vec{e}_y\) komplanar sind.
Aufgabensammlung
Mini-Test
Um Zugang zum Mini-Test zu kriegen,
musst du vollwertiges Mitglied im Hacker-Club sein.
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt









Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.