Inhalt
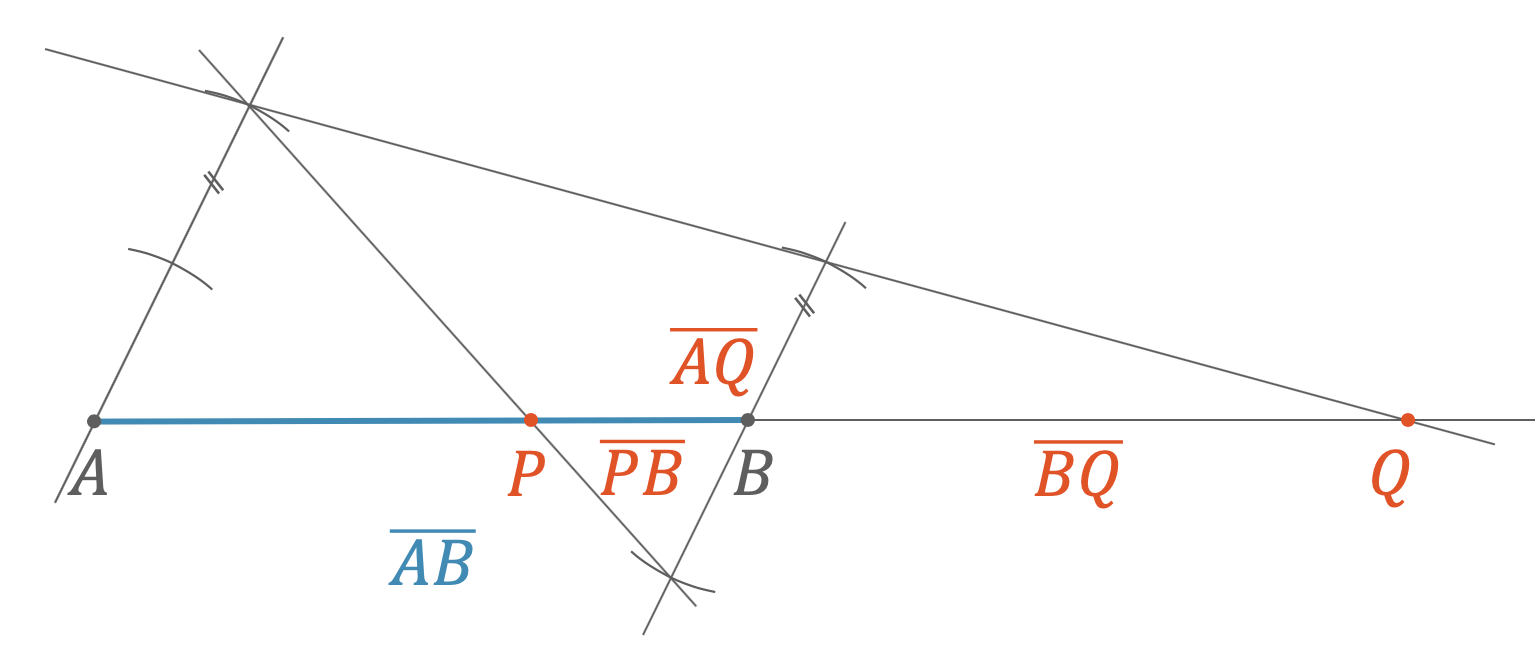
Wenn wir die innere und die äussere Teilung einer Strecke mit dem gleichen Verhältnis durchführen, wird die Strecke harmonisch geteilt mit den beiden Teilungspunkten \(P\) und \(Q\). Die Verhältnisse der Teilstrecken sind:
\[ \frac{\;\overline{AP}\;}{\overline{PB}} = \frac{\;\overline{AQ}\;}{\overline{BQ}} \]
Anwendung
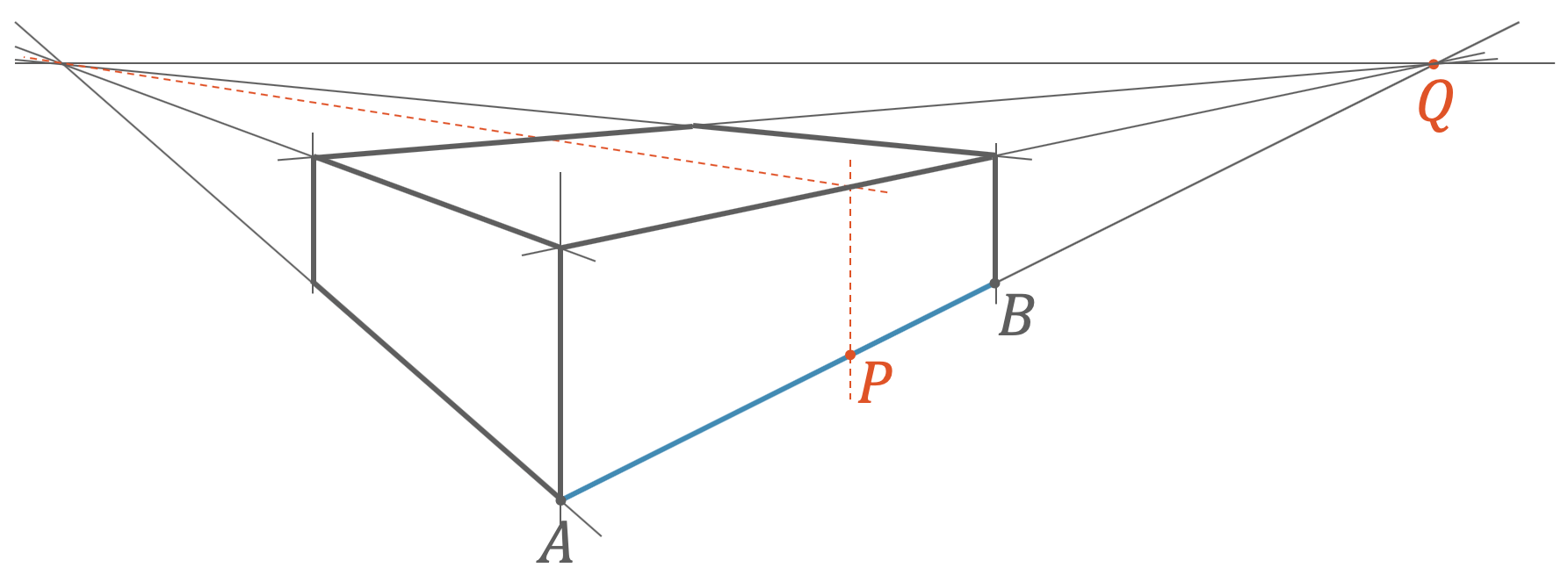
Mit Hilfe der harmonischen Teilung kann die Aufteilung einer Strecke in zwei gleich lange Teilstrecken in die zentralperspektivische Darstellung übertragen werden. Im unten dargestellten Beispiel wird der Quader in der halben Länge aufgeteilt. Perspektivisch erscheint die hintere Hälfte etwas kürzer als die vordere Hälfte, da sie schon weiter hinten ist. Wie viel kürzer? Nun, mit der harmonischen Teilung der Strecke \([AB]\) im Verhältnis \(2:1\) erhalten wir die Punkte \(P\) und \(Q\). Der Erstere gibt uns die Aufteilung der Quaders. Der andere Punkt \(Q\) entspricht dem Fluchtpunkt.
Weitere Videos
-
Harmonische Teilung: Berechnungen und Konstruktion (5001-5)
14 min 44 s
Du musst dich hier einloggen, um zum Video zu gelangen.
Noch kein Login?
Aufgabensammlung
-
Teilung einer Strecke (5001) – Aufg. 5
3 Teilaufgaben (pdf/Video-Lösung):
Harmonische Teilung: Berechnungen und KonstruktionDu musst dich hier einloggen, um zur Aufgabe zu gelangen.
Noch kein Login?
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt
Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.