Appolloniuskreis

Appolloniuskreis als Punktschar

Der Appolloniuskreis wird auch Kreis des Apollonios, Kreis des Apollonius oder apollonischer Kreis genannt.

Appollonius von Perga (im heutigen Anatolien) war ein griechischer Geometer und Astronom, der Ende drittes, Anfang zweites Jahrhundert vor Christus lebte.

Er ging mit der harmonischen Teilung noch einen Schritt weiter und überlegte sich, wo alle Teilungspunkte wohl liegen würden, deren Abstände zu den Endpunkten der zu teilenden Strecke das gleiche Verhältnis zu einander haben.

Der Appolloniuskreis ist diese Punktschar aller Teilungspunkte (inkl. \(P\) und \(Q\) der harmonischen Teilung), deren Abstände zu den Endpunkten \(A\) und \(B\) einer Strecke immer im gleichen Verhältnis \(a:b\) stehen.

Eine Strecke wird in einem bestimmten Verhältnis geteilt.

Zu dieser Strecke und diesem Teilungsverhältnis gibt es einen Appolloniuskreis als Punktschar aller möglichen Teilungspunkte.

Jeder Punkt auf dem Kreis hat zu den beiden Endpunkten der Strecke je einen Abstand, die im Teilungsverhältnis zueinander stehen.

Konstruktion

• Konstruiere zuerst die beiden Teilungspunkte \(P\) und \(Q\) der harmonischen Teilung.
• Halbiere mit dem Zirkel den Abstand \(\overline{PQ}\) und ermittle so das Zentrum \(M\) des Kreises
• Ziehe den Kreis mit Radius \(\overline{MP}\) bzw. \(\overline{MQ}\)

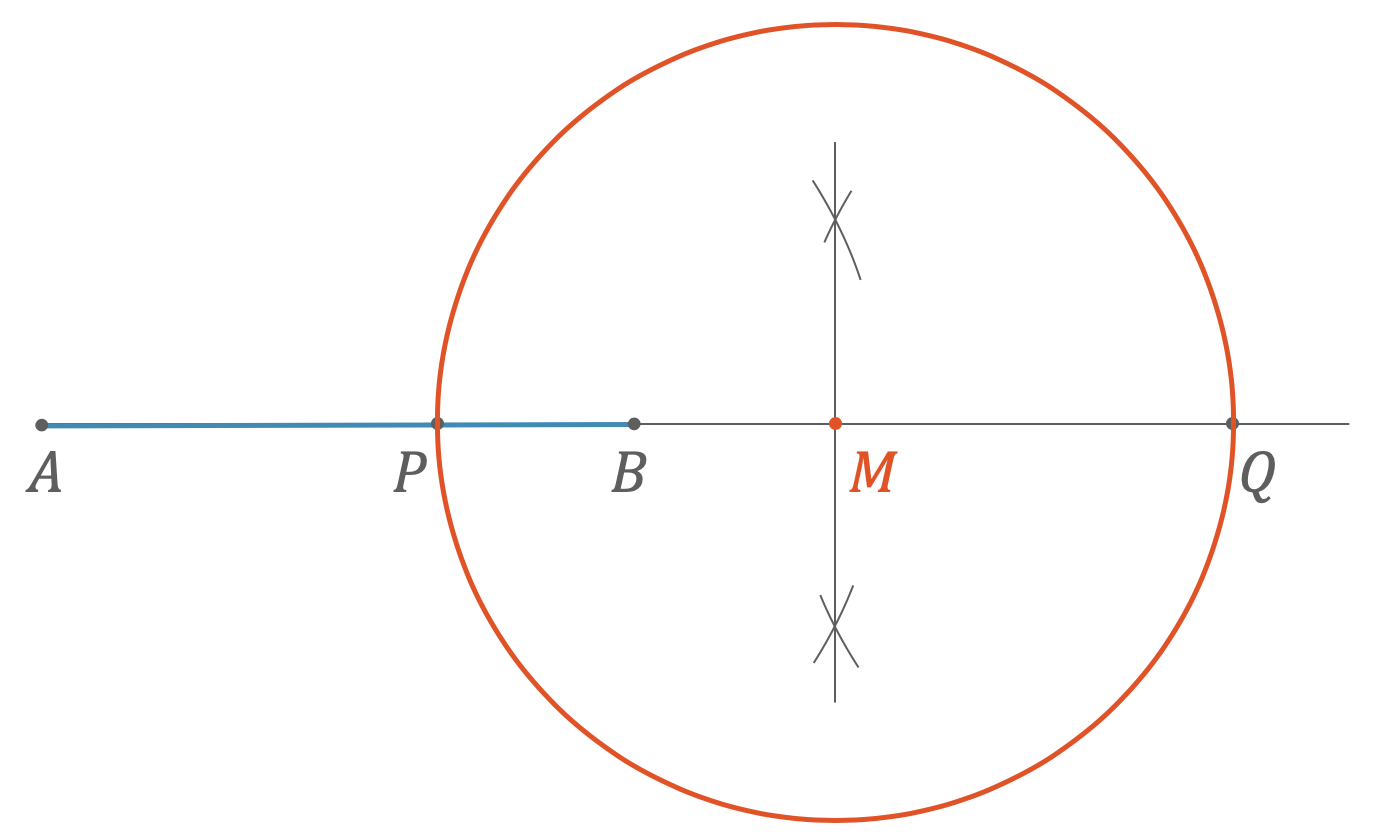
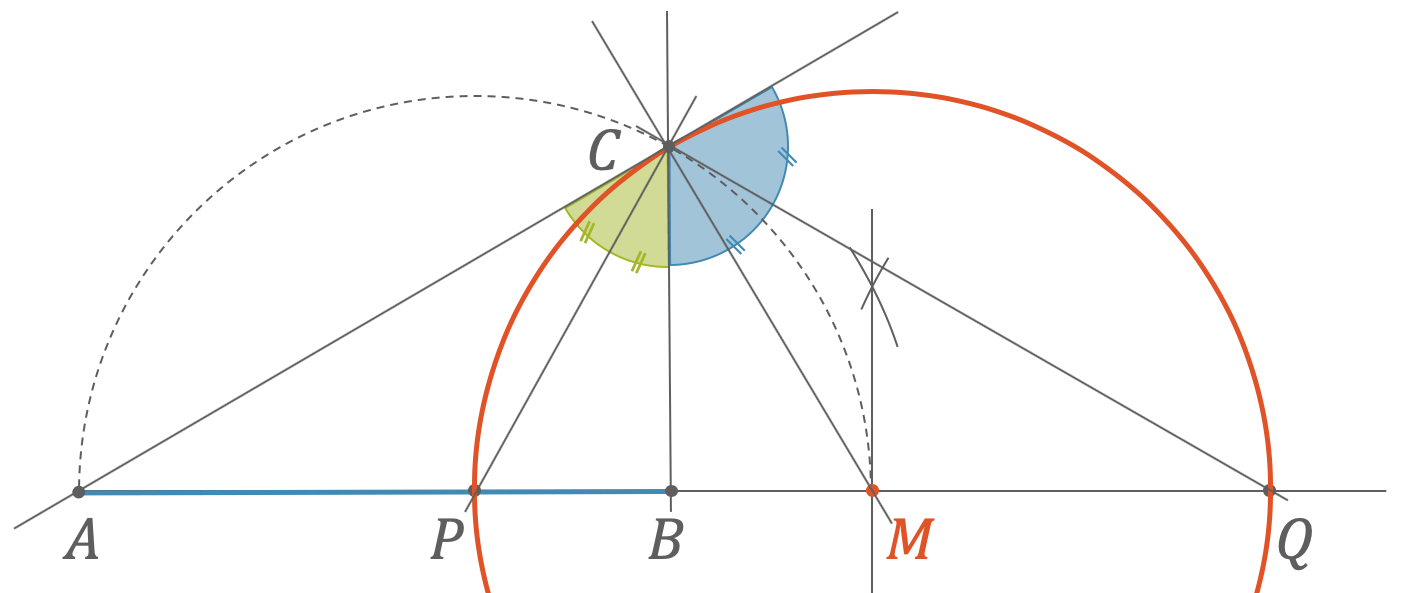
Beachte, dass wir mit einem Thaleskreis über \(AM\) eine Tangente an den Appolloniuskreis legen können. Diese Tangente berührt den Appolloniuskreis im Punkt \(C\).

Von diesem Punkt aus schliessen die Verbindungen \(CA\) und \(CB\) einen grünen Winkel ein. Die Verbindung \(CP\) ist die Winkelhalbierende, die den Winkel in der Mitte schneidet. Auf der anderen Seite wird der blaue Winkel durch die Verbindung \(CQ\) halbiert.