Trigonometrische Funktionen

Anwendung und Bedeutung

Die trigonometrischen Funktionen sind das Wundermittel für Berechnungen in der Geometrie. Man kann mit ihnen fast alle geometrischen Probleme lösen bzw. berechnen.

Wir schauen uns zuerst die Situation im rechtwinkligen Dreieck an, wo sie definiert sind. Es ist wichtig, dass wir diese Anwendung im rechtwinkligen Dreieck gut verstehen und sie uns auch gut einprägen.

Wir werden später in einem geometrischen Problem wie folgt vorgehen:

• Rechtwinkliges Dreieck suchen
• Falls kein rechtwinkliges Dreieck gefunden wurde, ein solches zeichnen ✍️, (z.B. durch Einführung einer Höhe, die rechtwinklig zu ihrer Grundseite steht)
• Aufstellen einer Gleichung ⚖️ mit Hilfe der Definition der trigonometrischen Funktionen

Definition der trigonometrischen Funktionen

In einem rechtwinkligen Dreieck haben die Seiten bestimmte Namen, die wir uns einprägen sollten:

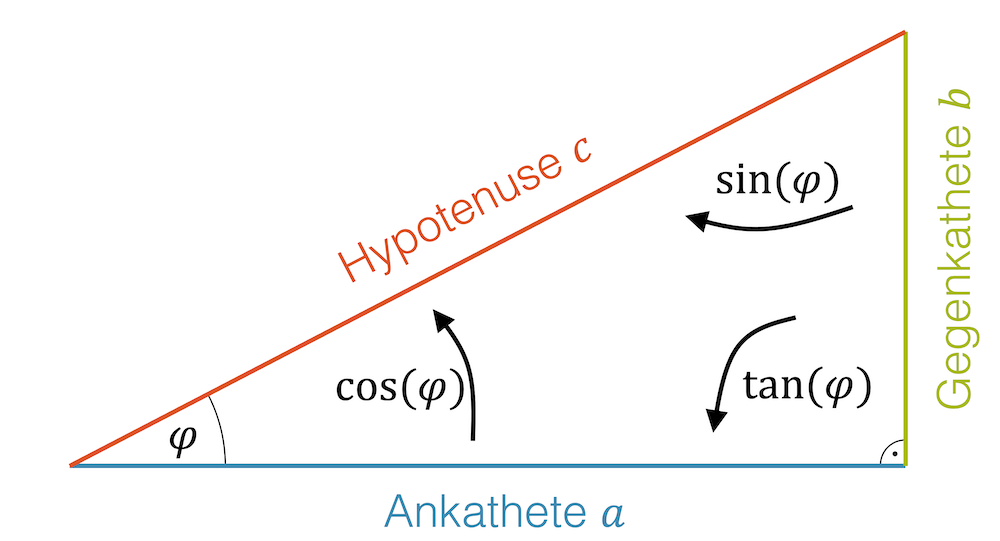
• Hypotenuse: Sie ist die längste Seite im rechtwinkligen Dreieck und steht dem rechten Winkel gegenüber.
• Ankathete: Die Kathete, die am betrachteten Winkel \(\alpha\) ist, heisst Ankathete.
• Gegenkathete: Sie steht dem betrachteten Winkel \(\alpha\) gegenüber.

Beachte: Hätten wir den anderen Winkel gewählt, hätten die beiden Katheten ihren Namen getauscht. Die Hypotenuse ist von der Wahl des Winkels nicht abhängig. Sie ist so oder so die längste Seite im Dreieck.

Die trigonometrischen Funktionen sind jetzt die folgenden Seitenverhältnisse:

Sinus: \(\sin(\alpha)=\frac{\text{Gegenkathete}}{\text{Hypotenuse}}\)

Kosinus: \(\cos(\alpha)=\frac{\text{Ankathete}}{\text{Hypotenuse}}\)

Tangens: \(\tan(\alpha)=\frac{\text{Gegenkathete}}{\text{Ankathete}}\)

Beachte, dass die Werte dieser Seitenverhältnisse und damit der Funktionswerte der trigonometrischen Funktionen unabhängig sind von der Grösse des Dreiecks, wohl aber von den Winkeln im Dreieck.

Wir werden das ausnützen, indem wir manchmal irgendein Dreieck mit falscher Grösse nehmen werden. Da es aber geometrisch ähnlich ist, hat es die gleichen Winkel und damit auch die gleichen Funktionswerte.

Im Einheitskreis

Wir betrachten jetzt den Einheitskreis im \(x,y\)-Koordinatensystem. Der Einheitskreis hat einen Radius von \(r=1\). Das ist besonders praktisch, wie wir gleich sehen werden. Nun wählen wir einen beliebigen Punkt A auf dem Kreis aus (siehe Abbildung).

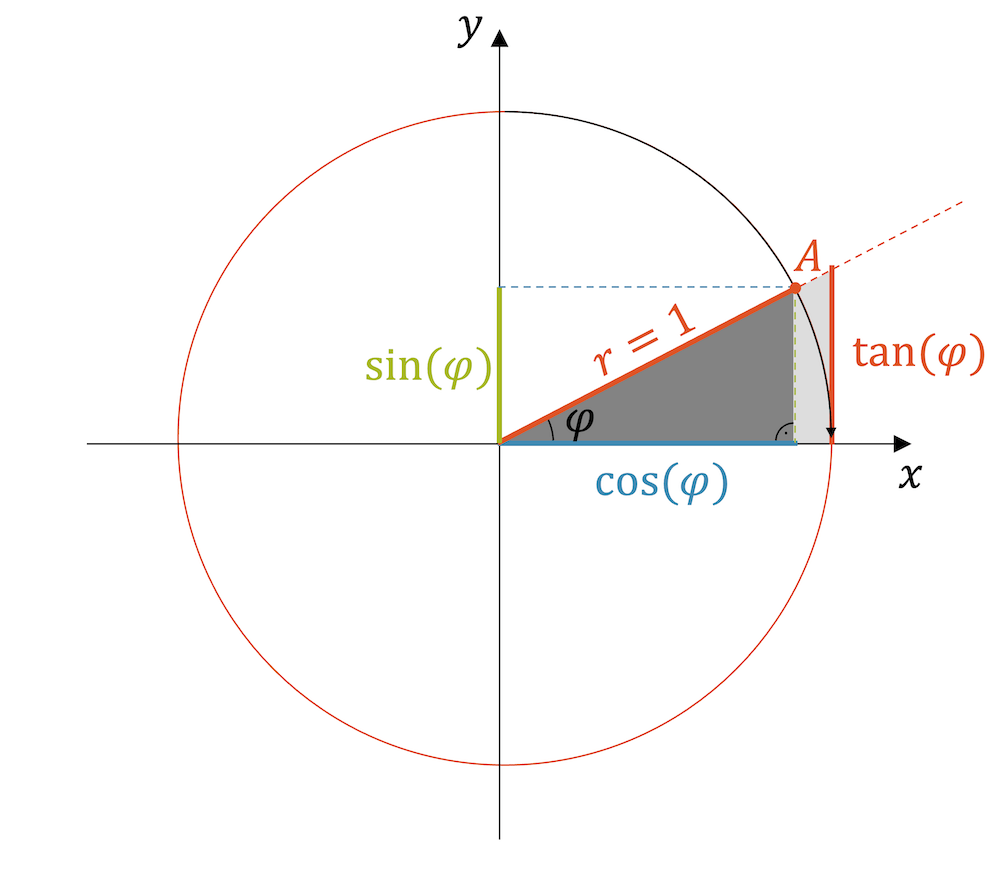
Wir können diesen Punkt eindeutig mit dem Winkel \(\varphi\) beschreiben und der zusätzlichen Bedingung, dass der Punkt auf dem Einheitskreis liegen muss.

Wenn wir den Punkt mit \(x,y\)-Koordinaten beschreiben möchten, benutzen wir die trigonometrischen Funktionen:

\[ A=\Bigl (\cos(\varphi),\sin(\varphi) \Bigr) \]

Wir wollen das kurz anhand der \(y\)-Koordinate überprüfen. Das Verhältnis von Gegenkathete zu Hypotenuse ist gleich dem Sinus von \(\varphi\). Die Hypotenuse ist 1, da es sich um den Einheitskreis handelt:

\[ \sin(\alpha)=\frac{b}{c}=\frac{b}{1}=b \]

Somit ist die Gegenkathete \(b\) gleich dem Sinus von \(\varphi\). Mit der gleichen Überlegung können wir schliessen, dass die Ankathete gleich dem Kosinus von \(\varphi\) ist.

Wie können wir den Tangens am Einheitskreis verstehen? Wir wissen ja, dass der Tangens das Verhältnis von Gegenkathete zu Ankathete ist. Im kleinen dunklen Dreieck gilt:

\[ \tan(\varphi)=\frac{\sin(\varphi)}{\cos(\varphi)} \]

Im grösseren, hellen Dreieck mit dem Einheitsradius als Ankathete gilt:

\[ \tan(\varphi)=\frac{\text{Gegenkathete}}{1} = \text{Gegenkathete} \]

Somit ist die Gegenkathete des hellen (grösseren) Dreiecks gleich dem Tangens von \(\varphi\).

Trigonometrische Funktionen für spezielle Winkel

Die trigonometrischen Funktionen haben wir im rechtwinkligen Dreieck definiert und ein solches rechtwinkliges Dreieck im Einheitskreis gefunden.

Wenn wir den Winkel \(\varphi\) nun grösser machen, erhalten wir für \(\varphi > 90^\circ\) ein stumpfes Dreieck. Für \(\varphi>180^\circ\) können wir schon gar nicht mehr von einem Dreieck sprechen, denn ein Winkel im Dreieck kann ja gar nicht grösser sein, als die Summe aller Winkel von 180°!

Dennoch können wir im Einheitskreis den Winkel \(\varphi\) beliebig gross oder klein, ja sogar negativ werden lassen (wenn wir im Uhrzeigersinn drehen).

Die Funktionswerte der trigonometrischen Funktionen sind dann wie folgt definiert:

• Sinus: \(y\)-Koordinate des Punkts A, wobei die Koordinaten oberhalb der \(x\)-Achse positiv, diejenigen unter der \(x\)-Achse negativ sind.
• Kosinus: \(x\)-Koordinate des Punkts A, wobei die Koordinaten rechts der \(y\)-Achse positiv, diejenigen links der \(y\)-Achse negativ sind.

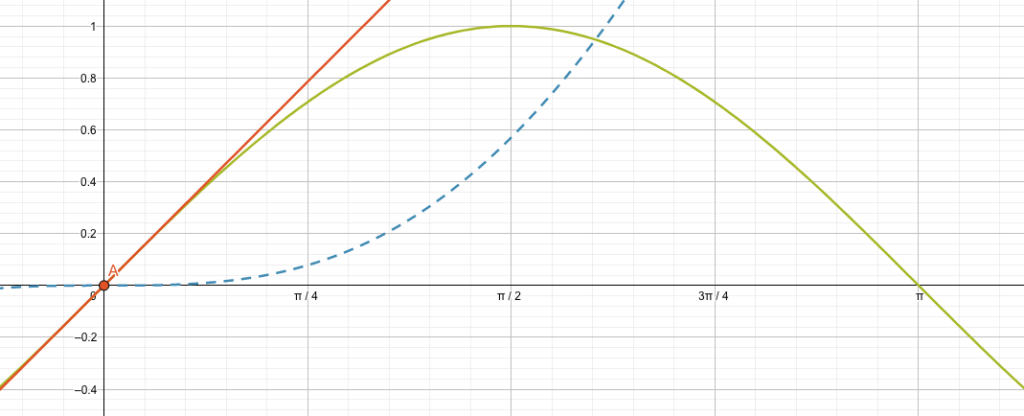
Für die Werte des Tangens erinnern wir uns daran, dass sie der Länge der Gegenkathete des hellen grossen Dreiecks entsprechen.

Diese wachsen für \(\varphi\) in der Nähe von 90° immer stärker an, d.h. sie werden für 90° unendlich gross:

\[ \lim_{\varphi \rightarrow 90^\circ}\big( \tan(\varphi) \big) \rightarrow \infty \]

Oberhalb der Unstetigkeit bei 90°, ist der Tangens negativ, denn der Tangens ist ja “Sinus durch Kosinus geteilt”. Der Sinus ist z.B. für 91° positiv, der Kosinus jedoch negativ. Der ganze Bruch (der Tangens) ist damit negativ.

Ableitung trigonometrische Funktionen

Dieser Artikel befasst sich im Speziellen mit der Ableitung der trigonometrischen Funktionen. Für Aufgabensammlungen, Lernziele, Mini-Tests etc. schaust du am besten im Hauptartikel zu den Ableitungsfunktionen nach.

Wie wir dort gesehen haben, ist die erste Ableitung der Sinus-Funktion gleich dem Kosinus. Andererseits ist die Ableitung der Kosinus-Funktion gleich dem Sinus mit (-1) multipliziert.

Ableitung trigonometrische Funktionen:

\[ \frac{d}{dx}\big( \sin(x) \big) \quad = \quad \cos(x) \]

\[ \frac{d}{dx}\big( \cos(x) \big) \quad = \quad -\sin(x) \]

\[ \frac{d}{dx}\big( \tan(x) \big) \quad = \quad \frac{1}{\cos^2(x)} \quad = \quad  1+\tan^2(x) \]

\[ \frac{d}{dx}\big( \cot(x) \big) \quad = \quad -\frac{1}{\sin^2(x)} \quad = \quad -\big(1+\cot^2(x)\big) \]