Tangens-Funktion
Während Sinus und Kosinus sich sehr ähneln, ist der Tangens dann doch ziemlich anders. Wir gehen wieder gleich vor und überlegen uns den Tangens für verschiedene Winkel \(\alpha\), den wir im Einheitskreis immer grösser wählen. Im Einheitskreis entspricht der Tangens der Länge der Gegenkathete des hellen, grösseren Dreiecks. Jedoch ist das Verhältnis von Gegenkathete zu Ankathete im hellen Dreieck gleich wie im dunkelgrauen Dreieck (Strahlensatz):
\[ \tan(\alpha) : 1 \quad = \quad \sin(\alpha) : \cos(\alpha) \]
Deshalb ist der Tangens auch gleich dem Verhältnis von Sinus zu Kosinus:
\[ \tan(\alpha) = \frac{\sin(\alpha)}{\cos(\alpha)} \]
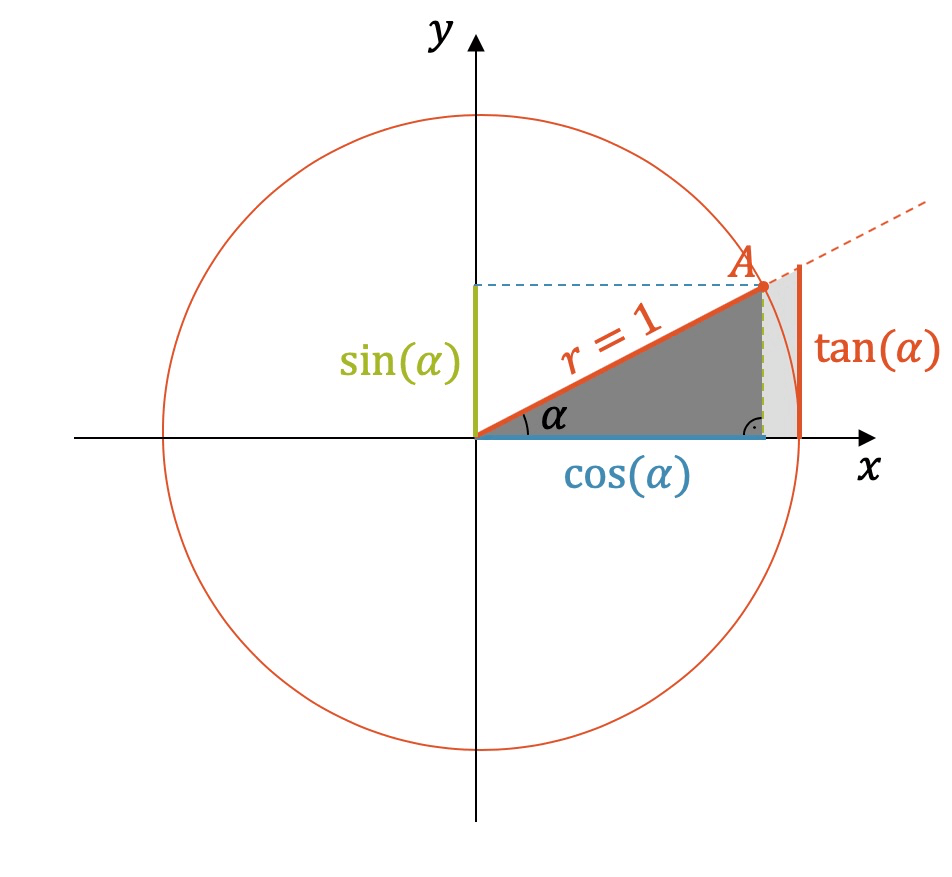
Bei \(\alpha= 0°\) haben wir natürlich null, weil die Ankathete dann null ist. Dann nimmt der Tangens zu. Bei \(\alpha=45°\) haben wir eine gleich lange Ankathete wie die Gegenkathete. Hier gilt also \(\tan(45°)=1\). Für \(\alpha=30°\) nehmen wir die Werte der Sinus- und Kosinusfunktion und setzen ein:
\[ \tan(30°) = \frac{\sin(30°)}{\cos(30°)} = \frac{\quad\frac{1}{2}\quad}{\frac{\sqrt{3}}{2}} = \frac{1}{\sqrt{3}} \]
Für den Winkel \(\alpha=60°\) gehen wir analog vor:
\[ \tan(60°) = \frac{\sin(60°)}{\cos(60°)} = \frac{\quad\frac{\sqrt{3}}{2}\quad}{\frac{1}{2}} = \sqrt{3} \]
Beachte, dass wir für \(\alpha>45°\) Tangenswerte haben, die grösser als 1 sind. Das ist ein erster grosser Unterschied zum Sinus und zum Kosinus: Der Tangens ist nicht auf einen ”Werte-Schlauch” beschränkt.
Wir machen jetzt \(\alpha\) immer grösser und stoppen kurz vor 90°. Die Gegenkathete des dunkelgrauen Dreiecks ist fast 1 und die Ankathete ist praktisch null. Der Tangens ist sehr sehr gross und ”explodiert” nächstens ins Unendliche.
Obwohl wir nicht durch null teilen dürfen, können wir sagen, dass die Zahl umso grösser wird, je näher wir an den Punkt \(\alpha=90°\) kommen. Was passiert aber, wenn der Winkel ganz leicht grösser als 90° ist? Die Gegenkathete ist immer noch fast 1, wenn auch ganz leicht kleiner. Die Ankathete bzw. der Kosinus ist nicht mehr null, aber immer noch sehr klein im Betrag. Neuerdings ist er aber negativ, d.h. das Vorzeichen des ganzen Bruchs wechselt.
Bei \(\alpha=90°\) haben wir eine Unstetigkeitsstelle, wo der Tangens von \(+\infty\) auf \(-\infty\) springt. Wir schreiben deshalb für den \(\tan(90°)\) in der Wertetabelle \(\pm\infty\). Das ist mathematisch gesehen etwas ”sloppy”, aber wir sind uns im klaren, dass der Tangens von 90° eigentlich gar nicht definiert ist, da wir durch null teilen müssten. Die kleine Wertetabelle für den Tangens sieht jetzt folgendermassen aus:
| \(\alpha\) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| \(x=\tan(\alpha)\) | 0 | \(\frac{1}{\sqrt{3}}\) | 1 | \(\sqrt{3}\) | \(\pm\infty\) | 0 | \(\pm\infty\) | 0 |
Der Graph der Tangens-Funktion ist in der folgenden Abbildung dargestellt. Wir erkennen sofort die Unstetigkeitsstellen bei -90°, 90°, 270° usw. Tatsächlich ”explodiert” der Tangens zu einer unendlich grossen Zahl, kommt dann aber gleich aus dem Minus-Unendlichen wieder hoch. Beachte bitte auch, dass der Tangens bei 45°, aber auch bei 180° + 45° = 225° genau +1 entspricht.
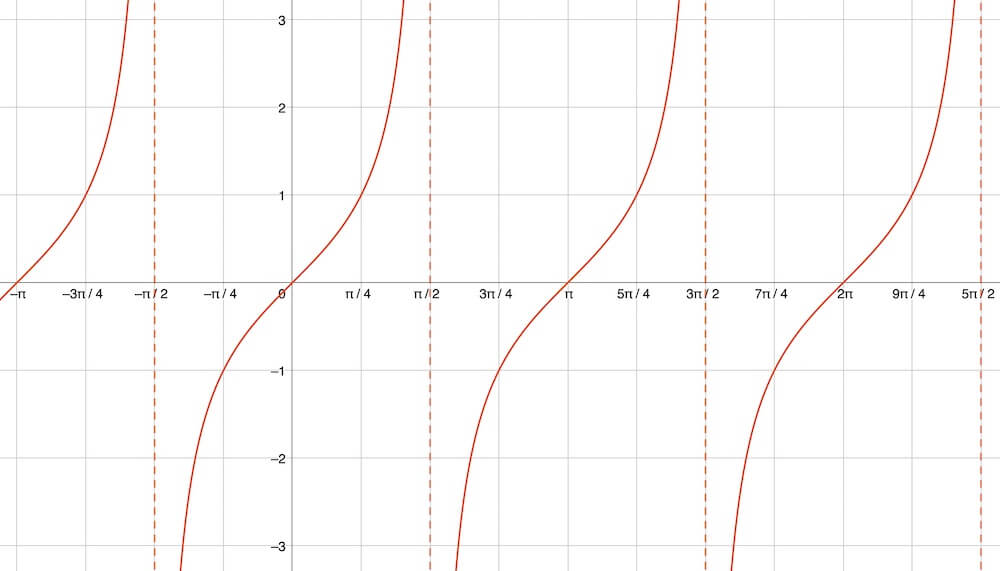
Eigenschaften der Tangens-Funktion:
- startet mit null: \(\tan(0)=0\)
- ”explodiert” bei 90° und wieder bei 270°, wobei das Vorzeichen an der Unstetigkeitsstelle wechselt
- Null-Durchgänge bei 0°, 180°, 360° etc.
- vollendet eine Periode bei 180° (!)
- ist eine ungerade Funktion: \(\tan(x)=-\tan(-x)\)
Kotangens-Funktion
Sobald irgendwo die Kotangens-Funktion auftaucht, verdrehen die meisten ihre Augen. Sie kann eigentlich nichts dafür und ist auch nicht viel schlimmer als die Tangens-Funktion, aber viele Anhänger hat sie definitiv nicht. Wir werden unsere Besprechung der Kotangens-Funktion deshalb auch möglichst kurz und schmerzlos halten.
Wir merken uns eigentlich nur folgendes:
Der Kotangens ist der Kehrwert des Tangens’
\[ \cot(\alpha) = \frac{1}{\tan(\alpha)} \]
Was passiert, wenn wir vom Tangens den Kehrbruch nehmen? Nun, jetzt entstehen die Unstetigkeitsstellen wo der Tangens null war, d.h. bei 0°, 180° 360° usw. Wo der Tangens klein war, ist der Kotangens gross und umgekehrt. Dort wo der Tangens wächst, nimmt der Kotangens im Betrag ab und natürlich auch umgekehrt. Die Steigung des Kotangens ist deshalb immer umgekehrt zur Steigung des Tangens.
Aus all diesen Überlegungen kriegen den folgenden Verlauf:
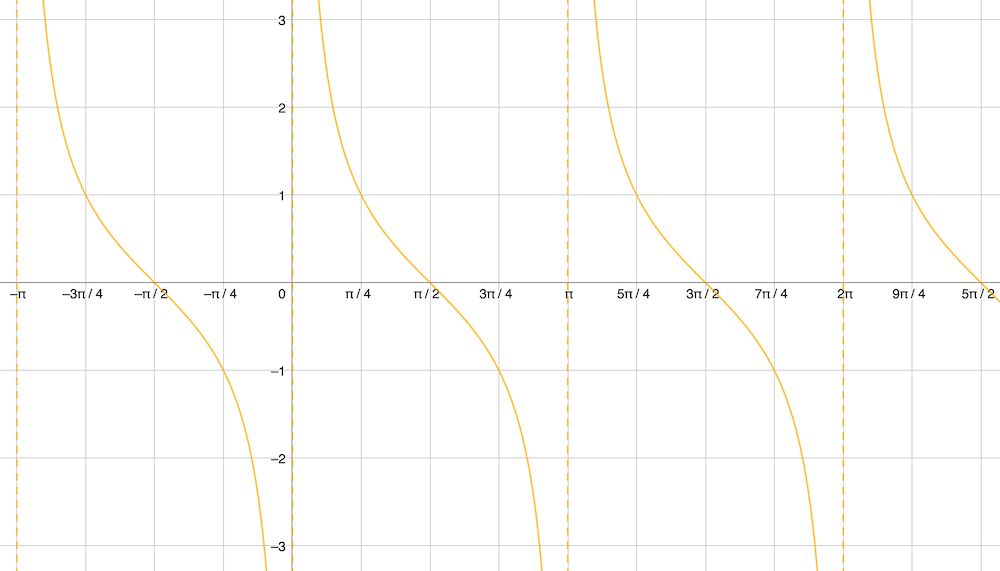
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.



Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.