Das Wichtigste in Kürze

Additionstheoreme der Trigonometrie:

\[ \sin^2(\alpha)+\cos^2(\alpha)=1 \]

\[ \sin(\alpha\pm\beta) = \sin(\alpha) \cdot \cos(\beta) \pm \cos(\alpha) \cdot \sin(\beta) \]

\[ \cos(\alpha\pm\beta) = \cos(\alpha) \cdot \cos(\beta) \mp \sin(\alpha) \cdot \sin(\beta) \]

In dieser kompakten Schreibweise werden entweder alle oberen oder alle unteren Vorzeichen benutzt.

Mit Hilfe dieser Formeln lassen sich auch Ausdrücke für doppelte, dreifache, halbe Winkel etc. finden. Dazu wird der Trick benutzt:

\[ \sin(2x) = \sin(x+x) \qquad \sin(x) = \sin\Big(\frac{x}{2}+\frac{x}{2}\Big) \]

Videos

    • Nachweis von trigonometrischen Identitäten (5039-1)

    • Nachweis einer trigonometrischen Identität (5039-2)

    Mit den Additionstheoremen haben wir ein paar wichtige Formeln zur Hand, die uns erlauben, trigonometrische Funktionen umzurechnen.

    “Mit Hilfe dieser Formel können wir jederzeit aus einem Sinus einen Kosinus machen oder umgekehrt!”

    Summe der Quadrate von Sinus und Kosinus

    Wenn wir uns den Einheitskreis anschauen und einen Punkt A festlegen, idealerweise mit einem nicht allzugrossen Winkel \(\varphi\), dann entspricht der Kosinus der \(x\)-Koordinate und der Sinus der \(y\)-Koordinate von A:

    \[ A\big(\cos(\varphi), \sin(\varphi)\big) \]

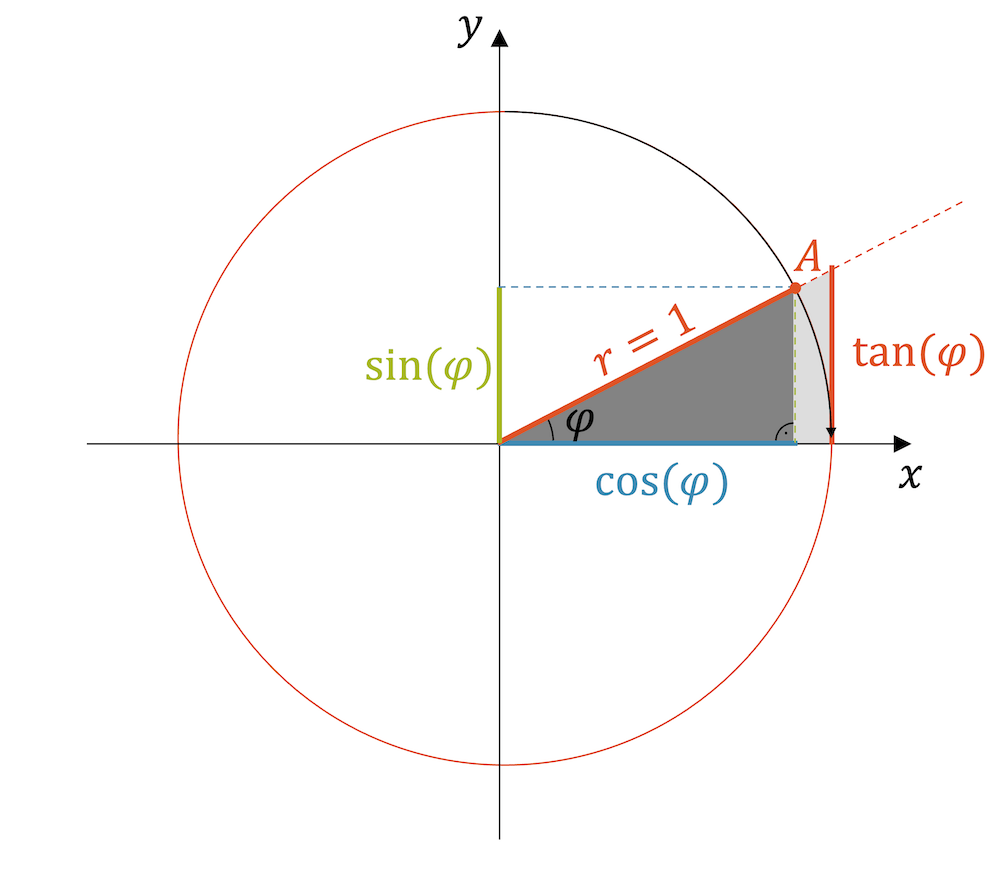
    Die Seiten des kleinen rechtwinkligen Dreieck (dunkel eingefärbt) haben die folgenden Längen:

    • Horizontale Kathete: \(a = \cos(\varphi)\)
    • Vertikale Kathete: \(b = \sin(\varphi)\)
    • Hypotenuse: \(c=1\) (da es der Einheitskreis ist)

    Wir stellen den Satz des Pythagoras \(a^2 + b^2 = c^2\) auf und setzen die Längen von oben ein:

    \[ \cos^2(\varphi) + \sin^2(\varphi) = 1^2 \]

    Für die allgemeine Formel wird meistens \(x\), statt \(\varphi\) verwendet, deshalb schreiben wir die gefundene Formel:

    \[ \cos^2(x) + \sin^2(x) = 1 \]

    Das Erstaunliche an dieser Formel: Sie gilt für alle \(x\)!

    Nicht nur für den spitzen Winkel, den wir für die Darstellung im Einheitskreis benutzt haben, sondern für alle möglichen \(x\)-Werte.

    Sinus einer Summe von zwei Winkeln

    Die nächsten zwei Formeln seien hier ohne Herleitung gegeben:

    \[ \sin(\alpha + \beta) = \sin(\alpha) \cdot \cos(\beta) + \cos(\alpha) \cdot \sin(\beta) \]

    \[ \sin(\alpha – \beta) = \sin(\alpha) \cdot \cos(\beta) – \cos(\alpha) \cdot \sin(\beta) \]

    Es ist üblich, hier eine kompakte Schreibweise für die Vorzeichen zu benutzen. Aus den beiden obigen Formeln machen wir so nur eine Zeile:

    \[ \sin(\alpha\pm\beta) = \sin(\alpha) \cdot \cos(\beta) \pm \cos(\alpha) \cdot \sin(\beta) \]

    So wird sie benutzt: Die Gleichung wird entweder mit allen oberen Vorzeichen oder mit allen unteren Vorzeichen.

    Beispiel

    Zeige, dass \(\;\; \sin(2x) = 2\sin(x)\cos(x)\;\;\) gilt.

    Wir benutzen das Additionstheorem für den Sinus mit dem oberen Vorzeichen, denn wir machen aus \(\sin(2x)\) einfach \(\sin(x+x)\):

    \[ \sin(x+x) = \sin(x) \cdot \cos(x) + \cos(x) \cdot \sin(x) \]

    Rechts stellen wir das Produkt noch um…

    \[ \sin(2x) = \sin(x) \cdot \cos(x) + \sin(x) \cdot \cos(x) \]

    …und erhalten direkt:

    \[ \sin(2x) = 2\sin(x)\cos(x) \]

    Kosinus einer Summe von zwei Winkeln

    Die Formel für den Kosinus führen wir hier auch ohne Herleitung ein:

    \[ \cos(\alpha\pm\beta) = \cos(\alpha) \cdot \cos(\beta) \mp \sin(\alpha) \cdot \sin(\beta) \]

    Auch hier enthält die Gleichung zwei Gleichungen in kompakter Schreibweise, entweder mit allen oberen Vorzeichen oder mit allen unteren Vorzeichen.

    Beispiel

    Zeige, dass \(\;\; \sin(x) = \cos(x-\frac{\pi}{2})\;\;\) gilt.

    Wir benutzen das Additionstheorem für den Kosinus mit den unteren Vorzeichen:

    \[ \cos(x-\frac{\pi}{2}) = \cos(x) \cdot \cos(\frac{\pi}{2}) + \sin(x) \cdot \sin(\frac{\pi}{2}) \]

    Jetzt setzen wir die Werte für \(\cos(\frac{\pi}{2})=0\) und \(\sin(\frac{\pi}{2})=1\) ein:

    \[ \cos(x-\frac{\pi}{2}) = \cos(x) \cdot 0 + \sin(x) \cdot 1 = \sin(x) \]

    Damit ist gezeigt, dass der nach rechts verschobene Kosinus dem Sinus entspricht.

    Beispiel

    Zeige, dass \(\;\; \sin^2(x) = \frac{1}{2}\cdot\bigl(1-\cos(2x)\bigr)\;\;\) gilt.

    Wir suchen eine Formel, in welcher \(\sin^2(x)\) vorkommt. Das Additionstheorem für den Kosinus hat diesen Term, sofern \(\alpha=\beta=x\):

    \[ \cos(\alpha + \beta) = \cos(\alpha) \cdot \cos(\beta) – \sin(\alpha) \cdot \sin(\beta) \]

    \[ \cos(x + x) = \cos^2(x) – \sin^2(x) \]

    Mit der bekannten Formel \(\sin^2(x)+\cos^2(x)=1\) ersetzen wir \(\cos^2(x)\) mit \(\bigl(1-\sin^2(x)\bigr)\):

    \[ \cos(2x) = \bigl(1-\sin^2(x)\bigr)- \sin^2(x) = 1 – 2\sin^2(x) \]

    Wir addieren \(2\sin(x)^2\) und subtrahieren \(\cos(2x)\):

    \[ 2\sin^2(x) = 1-\cos(2x) \]

    \[ \sin^2(x) = \frac{1}{2}\cdot\bigl(1-\cos(2x)\bigr) \]

    Doppelte, dreifache oder halbe Winkel

    In den bisherigen Beispielen haben wir den Trick 🪄 des doppelten Winkels schon verwendet, z.B.

    \[ \sin(2x) = \sin(x+x) \]

    Das erlaubt uns dann die Additionstheoreme zu zücken und einen Ausdruck mit dem einfachen Winkel \(x\) zu finden.

    Was machen wir, wenn wir einen dreifachen Winkel in der trigonometrischen Funktion haben? Da müssen wir einfach den Vorgang zwei Mal wiederholen.

    Beispiel: Sinus eines dreifachen Winkels

    Finde eine Formel mit einfachen Winkeln \(x\) für:

    \[ \sin(3x) \]

    Wir machen folgenden Split: \(\sin(3x) = \sin(x+2x)\) und wenden das Additionstheorem für den Sinus an:

    \[ \sin(x+2x) = \sin(x)\underline{\cos(2x)} + \cos(x)\underline{\sin(2x)} \]

    Jetzt berechnen wir als Zwischenresultat die beiden unterstrichenen Funktionen. Starten wir mit dem Kosinus mit zweifachem Winkel:

    \[ \underline{\cos(2x)} = \cos(x)\cos(x) – \sin(x)\sin(x) = \cos^2(x) – \sin^2(x) \]

    Das Gleiche machen wir für den Sinus des zweifachen Winkels:

    \[ \underline{\sin(2x)} = \sin(x)\cos(x) + \cos(x)\sin(x) = 2\sin(x)\cos(x) \]

    Dann setzen wir diese beiden Zwischenresultate oben ein:

    \[ \sin(3x) = \sin(x)\cdot\Big(\cos^2(x) – \sin^2(x)\Big) + \cos(x)\cdot\Big(2\sin(x)\cos(x)\Big) \]

    \[ = \sin(x)\cos^2(x) – \sin^3(x) + 2\sin(x)\cos^2(x) \]

    \[ = 3\sin(x)\cos^2(x) – \sin^3(x) \]

    Nun ersetzen wir mit \(\sin^2(x) + \cos^2(x) = 1\) bzw. \(\cos^2(x) = 1 – \sin^2(x)\) den Kosinus im Quadrat:

    \[ = 3\sin(x) \cdot \Big( 1- \sin^2(x) \Big) – \sin^3(x) \]

    \[ = 3\sin(x) – 3\sin^3(x) – \sin^3(x) \]

    Schliesslich erhalten wir:

    \[ \underline{\sin(3x) = 3\sin(x) -4\sin^3(x)} \]

    Für halbe Winkel benutzen wir die gleiche Idee umgekehrt: 🙃

    \[ \sin(x) = \sin\Big(\frac{x}{2}+\frac{x}{2}\Big) \]

    Es ist ein bisschen trickreicher, weil wir jetzt auf der anderen Seite der Additionstheoreme anfangen.

    Es empfiehlt sich mit dem Additionstheorem des Kosinus zu arbeiten. Beispielsweise kann ich schreiben:

    \[ \cos(x) = \cos(\frac{x}{2}+\frac{x}{2}) = \cos^2(\frac{x}{2}) – \sin^2(\frac{x}{2}) \]

    Beispiel: Sinus eines halben Winkels

    Finde eine Formel mit einfachen Winkel \(x\) für:

    \[ \sin\Big(\frac{x}{2}\Big) \]

    Wir benutzen \(\cos(x) = \cos(\frac{x}{2}+\frac{x}{2})\).

    Warum starten wir mit dem Kosinus? Weil das Additionstheorem des Kosinus auf der rechten Seite die Quadrate von Sinus und Kosinus hat. Das ist praktischer als die Mischterme im Additionstheorem des Sinus.

    \[ \cos\Big(\frac{x}{2}+\frac{x}{2}\Big) = \cos^2\Big(\frac{x}{2}\Big) – \sin^2\Big(\frac{x}{2}\Big) \]

    Um aus dem Kosinus einen Sinus zu machen, benutzen wir wieder \(\sin^2(x)+\cos^2(x)=1\), halt einfach mit dem halben Winkel \(\frac{x}{2}\) statt \(x\):

    \[ \cos(x) = \Big( 1 – \sin^2\Big(\frac{x}{2}\Big) \Big) – \sin^2\Big(\frac{x}{2}\Big) = 1 – 2\sin^2\Big(\frac{x}{2}\Big) \]

    Wir vertauschen die Seiten, subtrahieren 1 und dividieren durch (-2):

    \[ 1 – 2\sin^2\Big(\frac{x}{2}\Big) = \cos(x) \]

    \[ -2\sin^2\Big(\frac{x}{2}\Big) = \cos(x) -1 \]

    \[ \sin^2\Big(\frac{x}{2}\Big) = -\frac{\cos(x)-1}{2} \]

    \[ \sin^2\Big(\frac{x}{2}\Big) = \frac{1-\cos(x)}{2} \]

    Schliesslich ziehen wir die Quadratwurzeln und fertig:

    \[ \underline{\sin\Big(\frac{x}{2}\Big)\;\;=\;\;\pm\sqrt{\frac{1-\cos(x)}{2}}} \]

    Aufgabensammlung

    • Additionstheoreme, Sinus- und Kosinussatz (5039) – Aufg. 1

      3 Teilaufgaben (pdf/Video-Lösung):
      Nachweis von trigonometrischen Identitäten

      zur Aufgabe

    • Additionstheoreme, Sinus- und Kosinussatz (5039) – Aufg. 2

      1 Aufgabe (pdf/Video-Lösung):
      Anspruchsvoll: Nachweis einer trigonometrischen Identität

      zur Aufgabe

    Lernziele

    • Du kennst die Formel mit den Quadraten von Sinus und Kosinus auswendig
    • Du verstehst die kompakte Schreibweise der Additionstheoreme der Trigonometrie (mit dem doppelten Vorzeichen) und kannst sie anwenden

    Weitere Links

    Trigonometrische Funktionen

    Beziehungen zwischen trigonometrischen Funktionen

    Formelsammlung Trigonometrie (Wikipedia)

    Feedback

    Post Feedback Form

    Autor dieses Artikels:

    David John Brunner

    Lehrer für Physik und Mathematik | Mehr erfahren

    Kontakt

    publiziert:

    überarbeitet:

    publiziert:

    überarbeitet:

    Frage oder Kommentar?

    Frage/Kommentar?

    Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.

    Schreibe einen Kommentar