Lösungsmengen

Die Lösung einer Gleichung oder einer Ungleichung kann auch als Menge ausgedrückt werden. Beim einfachen Beispiel der Gleichung \(x+1=4\) ist die einzige Lösung \(x=3\). In der Mengenschreibweise sagen wir: “Die Menge aller Lösungen \(\boldsymbol{L}\) enthält das Element 3”

\[ \boldsymbol{L} = \bigl \{ 3 \bigr \} \]

Das bringt in diesem Fall keine Vorteile, ist aber bei Gleichungen mit mehreren Lösungen sehr praktisch.

Beispiel

Was sind die Lösungen der Gleichung \(x^4=16\)?

---

Wir wissen, dass \(2^4=16\) ist, somit ist \(x=2\) sicher eine Lösung. Bei Potenzen mit geraden Exponenten besteht aber immer auch die Möglichkeit, dass ein Vorzeichenwechsel stattgefunden hat. Tatsächlich ist auch \((-2)^4=16\), so dass \(x=(-2)\) auch eine Lösung ist.

Die Lösungsmenge ist deshalb:

\[ \boldsymbol{L} = \underline{\bigl \{ 2, -2 \bigr \}} \]

Der grösste Nutzen der Lösungsmenge sehen wir aber bei Ungleichungen. Nehmen wir einmal die folgende Ungleichung:

\[ x > x^2-4x+4 \]

Wir benutzen die grafische Methode und stellen dazu wieder eine Gleichung für die linke und eine Gleichung für die rechte Seite auf:

\[ y_1=x \]

\[ y_2= x^2-4x+4 \]

Dieses Mal haben wir die beiden Seiten nicht gleich \(y\) genannt, da sie nicht unbedingt gleich sein müssen. Die Ungleichung von oben lautet jetzt:

\[ y_1 > y_2 \]

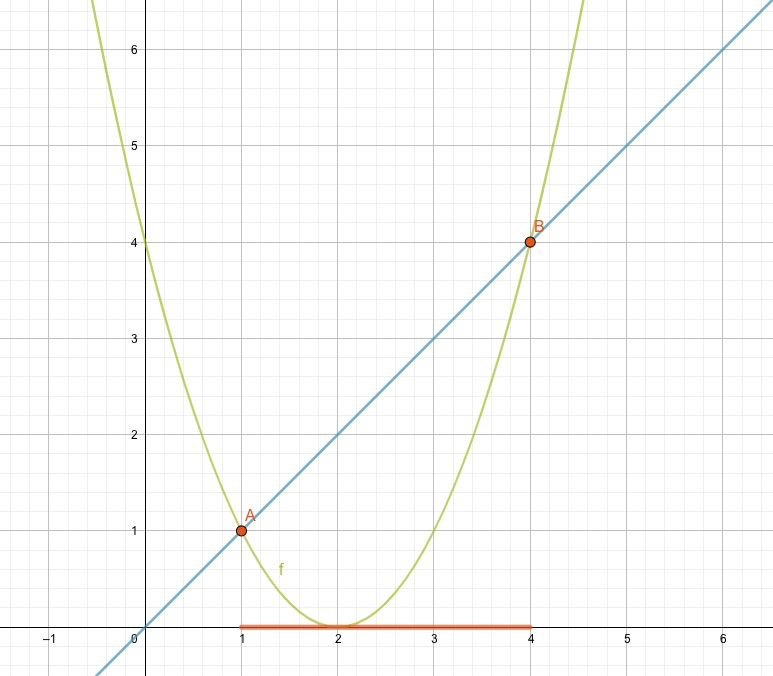
In der Abbildung sind die beiden Verläufe für \(y_1\) und \(y_2\) aufgezeichnet. \(y_1\) ist die blaue Linie, \(y_2\) ist als grüne Kurve dargestellt. Die Ungleichung verlangt \(y_1 > y_2\), d.h. blau soll höher liegen als grün. Für welche Werte unserer Unbekannten \(x\) ist diese Bedingung erfüllt?

Grafisch sehen wir das sofort, dass im Bereich zwischen 1 und 4 die grüne Kurve unter die blaue Linie zu liegen kommt und somit die Ungleichung erfüllt.

Die Lösungen für \(x\) sind alle Werte zwischen dem Schnittpunkt A und dem Schnittpunkt B. Sie sind in der Abbildung rot eingefärbt. Wie können wir diese Schar roter Lösungspunkte mit einer Lösungsmenge niederschreiben? Das Problem liegt darin, dass die Punkte unendlich zahlreich sind und wir sie nicht alle aufzählen können. Die Lösungen sind reelle Zahlen (\(\mathbb{R}\)), die ja unendlich nahe bei einander liegen.

Für solche Fälle benutzen wir die sog. Intervall-Schreibweise. Die Lösungen liegen in unserem Beispiel zwischen den Punkten A (\(x=1\)) und B (\(x=4\)). Wir schreiben deshalb:

\[ \boldsymbol{L} = \,\, ] 1,4 [ \]

Die eckigen Klammern sind absichtlich “verkehrt” geschrieben. Sie deuten damit an, dass die Werte \(x=1\) und \(x=4\) nicht zum Intervall und somit zu den Lösungen gehören: Sie sind von der Lösungsmenge ausgeschlossen. Die Ungleichung verlangt ja, dass \(y_1 > y_2\). Für \(x=1\) und \(x=4\) gilt jedoch \(y_1 = y_2\), was die Ungleichung nicht erfüllt. Die Ungleichung ist erfüllt, sobald \(x\) nur ein ganz kleines Bisschen über der Grenze 1 oder unter der Grenze 4 liegt.

Beispiel

Was ist die Lösungsmenge \(\boldsymbol{L}\) für folgende Ungleichung?

\[ x^2-4x+4 \leq 1 \]

---

In der Abbildung von oben haben wir den Verlauf der linken Seite in grün. Nun schauen wir, für welche \(x\) diese grüne Kurve gleich oder unter dem Wert von 1 liegt. Aus der Grafik lesen wir ab, dass die beiden Schnittpunkte (1,1) und (3,1) sind. Die Lösungen liegen deshalb im Intervall zwischen \(x=1\) und \(x=3\).

Da die linke und die rechte Seite der Ungleichung auch gleich sein dürfen, sind die Schnittpunkte dieses Mal Teil der Lösung. Die Lösungsmenge ist deshalb:

\[ \boldsymbol{L}=[1,3] \]