Inhalt
Das Wichtigste in Kürze
Streckung des Funktionsverlaufs in vertikaler Richtung:
Die Original-Funktion sei \(f(x)\). Wir können einen neuen Funktionsgraphen \(g(x)\) erhalten, der um den Faktor \(\boldsymbol{k}\), von der \(x\)-Achse aus, in vertikaler Richtung gestreckt ist, mit:
\[ g(x)=\boldsymbol{k} \cdot f(x) \]
Wenn \(\boldsymbol{k}<1\) ist, wird die Funktion entsprechend gestaucht. Der Faktor der Stauchung entspricht dem Kehrwert \(\frac{1}{k}\).
Stauchung des Funktionsverlaufs in horizontaler Richtung:
Aus der Funktion \(f(x)\) erhalten wir die neue Funktion \(g(x)\), die um \(\boldsymbol{k}>1\) in der Horizontalen gestaucht ist, mit:
\[ g(x)=f(\boldsymbol{k} \cdot x) \]
Wenn der Graph um den Faktor \(\boldsymbol{k}>1\) in der Horizontalen gestreckt werden soll, multiplizieren wir das Argument mit dem Kehrwert \(\frac{1}{k}\)
\[ g(x)=f(\frac{1}{\boldsymbol{k}} \cdot x) \]
Tutorial Videos
(Es gibt leider keine Tutorial Videos zu diesem Thema)
Häufigste Fragen
Funktionen vertikal strecken und stauchen
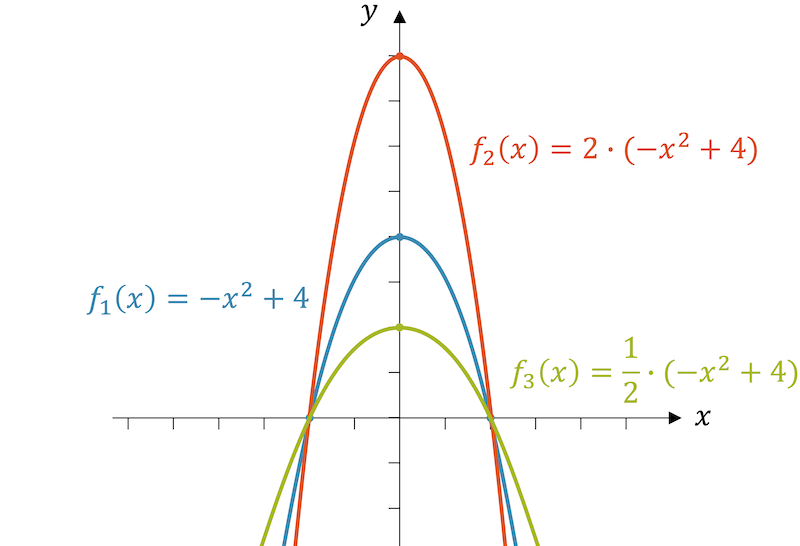
Wenn wir jeden Funktionswert mit einem Faktor \(k\) multiplizieren, dann wird der Verlauf der Funktion von der \(x\)-Achse her nach oben gestreckt.
Sie wird aber auch unterhalb der \(x\)-Achse nach unten gestreckt, denn die negativen Funktionswerte werden mit den Streckfaktor multipliziert und sind dann noch negativer.
Streckung des Funktionsverlaufs in vertikaler Richtung:
Die Funktionswerte der Original-Funktion \(f(x)\) werden mit dem Faktor \(k\) multipliziert. Wir erhalten so einen neuen Funktionsgraphen \(g(x)\), der um den Faktor \(\boldsymbol{k}\) in vertikaler Richtung gestreckt ist:
\[ g(x)=\boldsymbol{k} \cdot f(x) \]
Wenn \(\boldsymbol{k}<1\) ist, wird die Funktion entsprechend gestaucht. Der Faktor der Stauchung entspricht dem Kehrwert \(\frac{1}{k}\).
Stauchung des Funktionsverlaufs in vertikaler Richtung mit Faktor \(k\) (Streckung mit Faktor \(\frac{1}{k}\)):
\[ g(x)=\frac{1}{\boldsymbol{k}} \cdot f(x) \]
Beispiel
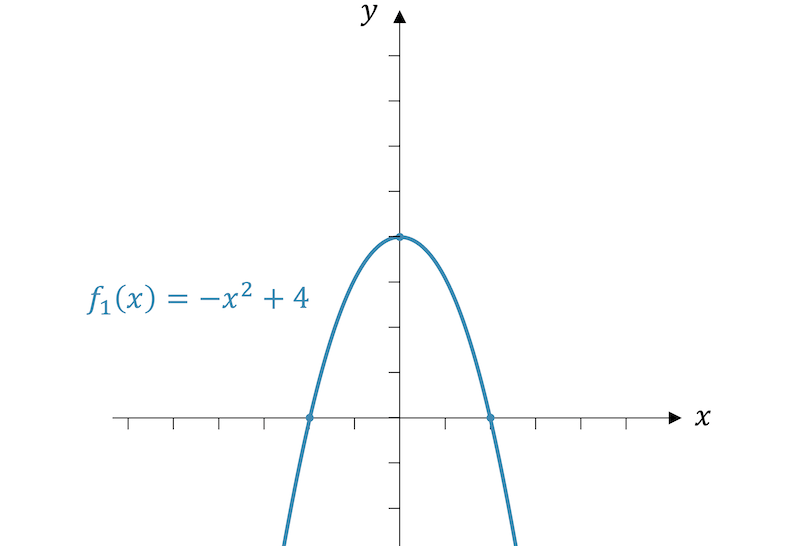
“Strecken und stauchen in der Horizontalen: Einfach die Änderung an der Funktionsvariablen (Argument) vornehmen und daran denken: Ist immer umgekehrt!”
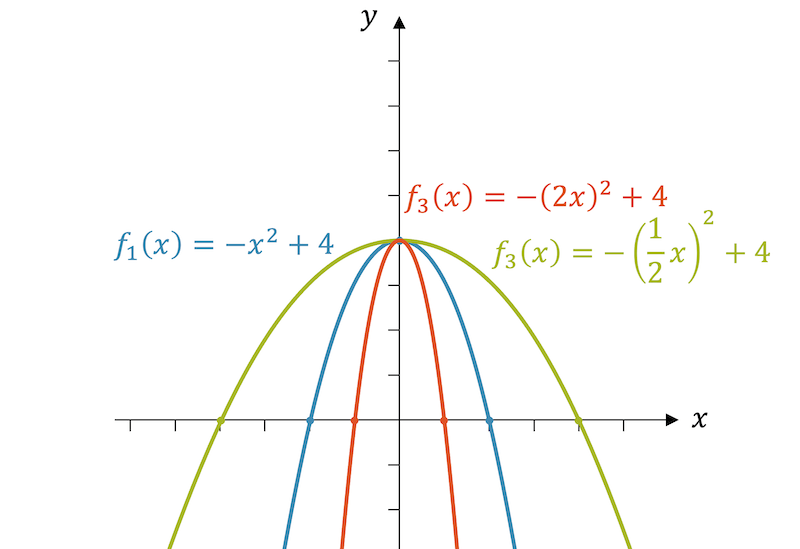
Funktionen horizontal strecken und stauchen
Wie schon beim Verschieben von Funktionen, müssen wir jetzt die Funktionsvariable \(x\) verändern, statt den Funktionswert \(y=f(x)\) und wir müssen umdenken, weil es immer etwas umgekehrt ist.
Eine Multiplikation der Funktionsvariablen \(x\) mit dem Streckfaktor \(k\) für jetzt zu einer horizontalen Stauchung:
\[ g(x)=f(\boldsymbol{k} \cdot x) \]
Wenn es uns aber um eine horizontale Streckung mit dem Faktor \(k\) geht, stauchen wir mit dem Kehrwert \(\frac{1}{k}\):
\[ g(x)=f(\frac{1}{\boldsymbol{k}} \cdot x) \]
Beispiel
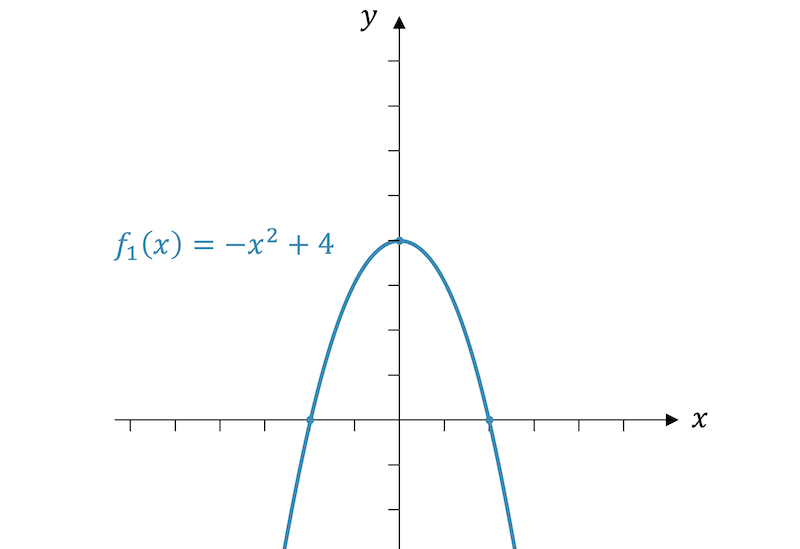
Weitere Videos
(keine externe Youtube-Videos zu diesem Thema)
Aufgabensammlung
Lernziele
Mini-Test
Um Zugang zum Mini-Test zu kriegen,
musst du vollwertiges Mitglied im Hacker-Club sein.
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt






Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.