Inhalt
Das Wichtigste in Kürze
Eine Funktion ist eine eindeutige Zuweisung von einem Element \(x\) aus dem Definitionsbereich \(\boldsymbol{D}\) zu einem Element \(y\) aus dem Wertebereich \(\boldsymbol{W}\).
Mathematisch wird die Zuweisung von \(x\) zu \(y\) aus der ersten Menge \(\boldsymbol{D}\) in die zweite Menge \(\boldsymbol{W}\) wie folgt geschrieben:
\[ f: \quad \boldsymbol{D} \rightarrow \boldsymbol{W},\;x \mapsto y \]
Die exakte Umkehrung der Zuweisung von \(f\) nimmt die Umkehrfunktion vor:
\[ f^{-1}: \quad \boldsymbol{W} \rightarrow \boldsymbol{D},\;y \mapsto x \]
Tutorial Videos
(Es gibt leider keine Tutorial Videos zu diesem Thema)
Die Zahlenmenge der Werte, die die Funktion aufnehmen kann, nennen wir Definitionsbereich \(\boldsymbol{D}\) und die Menge der Zahlen, die die Funktion ausgibt, den Wertebereich \(\boldsymbol{W}\). In unserer Analogie umfasst \(\boldsymbol{D}\) alle Arten von Münzen, die der Automat akzeptiert und \(\boldsymbol{W}\) enthält alle Produkte des Automaten.
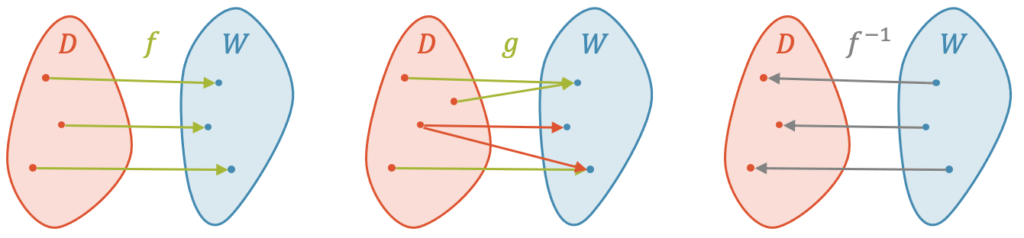
In der linken Skizze ordnet die Funktion \(f\) jedem der drei Argumente einen eindeutigen Funktionswert zu. Die Skizze ganz rechts zeigt die Umkehrfunktion \(f^{-1}\). Sie existiert, da die Zuweisungen eindeutig umkehrbar sind.
Die mittlere Skizze zeigt uns die Funktion \(g\) und zwei wichtige Spezialfälle:
- Verschiedene Werte in \(\boldsymbol{D}\) werden dem gleichen Wert in \(\boldsymbol{W}\) zugewiesen: Das ist zulässig.
- Ein Wert in \(\boldsymbol{D}\) wird verschiedenen Werten in \(\boldsymbol{W}\) zugewiesen (rot). Das ist nicht zulässig, denn dadurch ist die Zuweisung nicht eindeutig definiert.
Funktionen müssen in der Mathematik immer eindeutig zuweisen. Wenn mehrere Argumente zum gleichen Funktionswert zugewiesen werden, dann ist das zulässig. Allerdings gibt es hierfür keine Umkehrfunktion \(g^{-1}\), da die Umkehrung nicht eindeutig wäre.
Beispiel
Eine Funktion \(f\) nimmt als Argument eine natürliche Zahl auf (Input). Sie gibt dann immer genau die Hälfte davon wieder heraus (Output): z.B. \(1\mapsto\frac{1}{2},\;2\mapsto 1,\; 3\mapsto \frac{3}{2},\;\) usw.
Wie lautet die Definition der Funktion (inkl. Definitions- und Wertebereich)?
Die Definitionsmenge entspricht der Menge der natürlichen Zahlen \(\mathbb{N}\). Die Werte, die die Funktion ausgibt sind aber nicht immer natürliche Zahlen. Es sind aber immer Brüche und somit rationale Zahlen der Menge \(\mathbb{Q}\). Die Funktion \(f\) ist wie folgt definiert:
\[ \underline{f:\;\;\mathbb{N}\rightarrow\mathbb{Q},\;x\mapsto\frac{x}{2}} \]
Mit dem speziellen Pfeil \((\mapsto)\) wird gezeigt, wie die Funktion \(f\) aus einem Argument \(x \in \mathbb{N}\) den Output \(\frac{x}{2} \in \mathbb{Q}\) produziert.
Weitere Videos
(keine externe Youtube-Videos zu diesem Thema)
Aufgabensammlung
Mini-Test
Um Zugang zum Mini-Test zu kriegen,
musst du vollwertiges Mitglied im Hacker-Club sein.
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt






Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.