Das Wichtigste in Kürze
Der Logarithmus ist eine andere Schreibweise für eine Potenz, die v.a. dann benutzt wird, wenn der Exponent gesucht ist:
\[ a^b = x \quad \leftrightarrow \quad \log_a(x) = b \]
Die Formulierung lautet wie folgt: “\(a\) hoch wie viel gibt uns das Argument \(x\)? Es ist \(b\)”.
Der Logarithmus kann eine beliebige Basis (positive) \(a\) haben, sofern die gleichen Anforderungen erfüllt sind, wie bei der Exponentialfunktion:
\[ a \in \mathbb{R}^+ , \quad a \neq 1 \]
Für die natürliche Basis \(e\) nennen wir den Logarithmus den natürlichen Logarithmus \(\log_e(x) = \ln(x)\):
\[ \ln(x) = b \quad \Leftrightarrow \quad e^b = x \]
Oft kommt auch der sog. Zehnerlogarithmus \(\log_{10}(x) = \lg(x)\) vor, dessen Basis \(a=10\) ist:
\[ \lg(x) = b \quad \Leftrightarrow \quad 10^b = x \]
Die Funktionswerte der Logarithmusfunktion sind in der Regel irrational und nur mit dem Taschenrechner zu berechnen.
Eigenschaften von Logarithmen für beliebige, jedoch zulässige Basen \(a\):
\[ \log_a(1) = 0 \]
\[ \log_a(a) = 1 \]
\[ log_a \big( a^x \big) = x \]
\[ a^{(\log_a(x))} = x \]
Erste Ableitung Logarithmusfunktion:
\[ \frac{d}{dx}\Big(\ln(x)\Big) = \frac{1}{x} \]
\[ \frac{d}{dx}\Big(\log_a(x)\Big) = \frac{1}{\ln (a) \cdot x} \]
Videos
Häufigste Fragen
Andere Schreibweise für eine Potenz
Der Logarithmus ist nichts anderes als eine andere Schreibweise für eine Potenz. Warum eine neue Schreibweise? Was bringt das?
Wenn wir Gleichungen lösen, dann ist die Unbekannte meistens in der Basis, z.B. \(x^2\) in einer quadratischen Gleichung. Eine solche Gleichung lösen wir mit einer Wurzel, übrigens ebenfalls eine andere Schreibweise für eine Potenz.
Bei Exponentialfunktionen ist die Unbekannte im Exponenten und wir können sie mit einem Logarithmus.
\[ a^b = x \quad \leftrightarrow \quad \log_a(x) = b \]
Wir lesen den Logarithmus wie folgt:
“\(a\) hoch wie viel gibt \(x\)? Die Lösung: \(a\) hoch \(b\) gibt \(x\).”
Auch wenn es am Anfang etwas komisch ist, gewöhnt man sich relativ schnell daran.
Aufgrund der Eigenschaften von Potenzen, kriegen wir folgende Identität, gültig für jede Basis \(a\):
\[ \log_a(1) = 0 \]
Diese Identität folgt direkt daraus, dass \(a^0 = 1\), egal wie gross \(a\) ist.
Aus \(a^1=a\) folgt die nächste Identität:
\[ \log_a(a) = 1 \]
Damit wissen wir, dass der Logarithmus von 1 immer null ergibt und dass wir 1 kriegen, wenn wir die Basis in den Logarithmus eingeben.
Beispiel: Einfachste Anwendung
Was ist der Wert von \(x\) in der folgenden Gleichung?
\[ 3^x = 243 \]
Beispiel: Einfache Berechnungen ohne Taschenrechner
Berechne für die folgenden einfachen Logarithmen die Unbekannte \(y\) ohne Taschenrechner:
\[ \text{a)} \;\; y = \log_2 (8), \quad \text{b)} \;\; \log_3 (y) = 3, \quad \text{c)} \;\; \log_y \Big (\frac{1}{2} \Big ) = 2 \]
Logarithmus als Umkehrfunktion
Wir wissen, dass der Logarithmus eigentlich zu einer Potenz gehört:
\[ \log_a(x) = b \quad \Leftrightarrow \quad a^b = x \]
Wenn wir die Potenz auf der rechten Seite als unsere Funktion \(f\) betrachten, dann weist sie dem Argument \(b\) den Funktionswert \(x\) zu. Sie nimmt ein \(b\) und macht daraus eine Potenz, deren Wert \(x\) entspricht:
\[ f: \; b \mapsto x, \quad f(b) = a^b = x \]
Der Logarithmus macht genau das Umgekehrte: Er nimmt das \(x\) und macht daraus das passende \(b\):
\[ f^{-1}: \, x \mapsto b, \quad f^{-1} = \log_a(x) = b \]
Deshalb ist der Logarithmus mit Basis \(a\) die Umkehrfunktion der Exponentialfunktion mit Basis \(a\).
Allgemein gilt, dass wenn wir eine Funktion und ihre Umkehrung gleich nacheinander ausführen, erhalten wir wieder das ursprüngliche Argument:
\[ f(b) = f\Big( f^{-1}(x)\Big) = x \]
\[ f^{-1}(x) = f^{-1}\Big( f(b)\Big) = b \]
Der Logarithmus ist die Umkehrfunktion der Exponentialfunktion mit der gleichen Basis:
\[ a^{\big( \log_a(x)\big)} = x \]
\[ \log_a\big( a^b \big) = b \]
Analog gilt es auch für den natürlichen Logarithmus…
\[ e^{\big( \ln(x)\big)} = x \]
\[ \ln\big( e^b \big) = b \]
…und für den Zehnerlogarithmus:
\[ 10^{\big( \lg(x)\big)} = x \]
\[ \lg\big( 10^b \big) = b \]
Beispiel: Zellteilungen
Wie viele Zellteilungen braucht es, damit aus einer Zelle mindestens Tausend bzw. eine Million Zellen entstanden sind?
Gleichungen mit Logarithmus lösen
Wenn wir eine Exponentialgleichung haben und die Unbekannte im Exponenten ist, können wir sie sehr einfach mit dem “Gegenmittel Logarithmus” 💊 lösen, wie wir im nachfolgenden Beispiel zeigen.
Beispiel: Lösen einer Exponentialgleichung
Welcher Wert von \(x\) erfüllt die folgende Gleichung?
\[ \frac{e^{(x+1)}}{3} = 1 \]
“Nichts steigt langsamer als der Logarithmus!”
Graph des Logarithmus
Da der Logarithmus die Umkehrfunktion der Exponentialfunktion (mit der gleichen Basis) ist, erhalten wir den Graphen des Logarithmus mit einer Spiegelung an der 45°-Geraden \((y=x)\).
Wir wählen die natürliche Basis \(e\) :
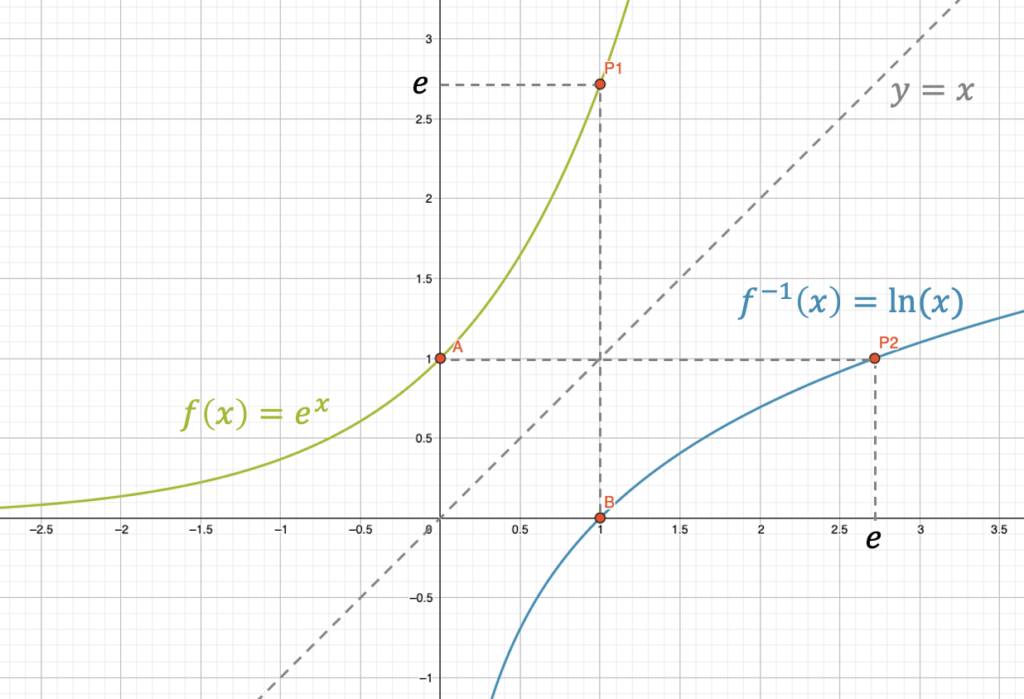
Wir sehen, dass der Logarithmus nur auf der rechten Hälfte vorkommt, d.h. nur für \(x>0\).
Für \(x\)-Werte, die nahe zu null liegen, fällt der Logarithmus fast senkrecht runter ins Negative. Das ist eine Asymptote, die wir wie folgt ausdrücken können:
\[ \lim_{x \rightarrow 0}\Big( \log(x) \Big) \rightarrow -\infty\]
Nach rechts steigt der Logarithmus und flacht immer mehr ab. Es wichtig zu wissen, dass er nie komplett abflacht, d.h. er steigt immer weiter, wenn auch immer weniger schnell.
Der Logarithmus ist, je weiter rechts wir gehen, die langsamste, steigende Funktion überhaupt!
Weil der Logarithmus aber trotz allem immer noch weiter steigt, gibt es keinen Grenzwert, den er anstrebt, sondern er steigt ins Unendliche:
\[ \lim_{x \rightarrow \infty}\Big( \log(x) \Big) \rightarrow +\infty\]
“Obwohl der Logarithmus immer mehr abflacht, erreicht er die Unendlichkeit…irgendwann…aber definitiv als letzter aller Funktionen.”
Beispiel: Graphen bestimmen
Bestimme die Basen der drei Logarithmusfunktionen im folgenden Graphen:
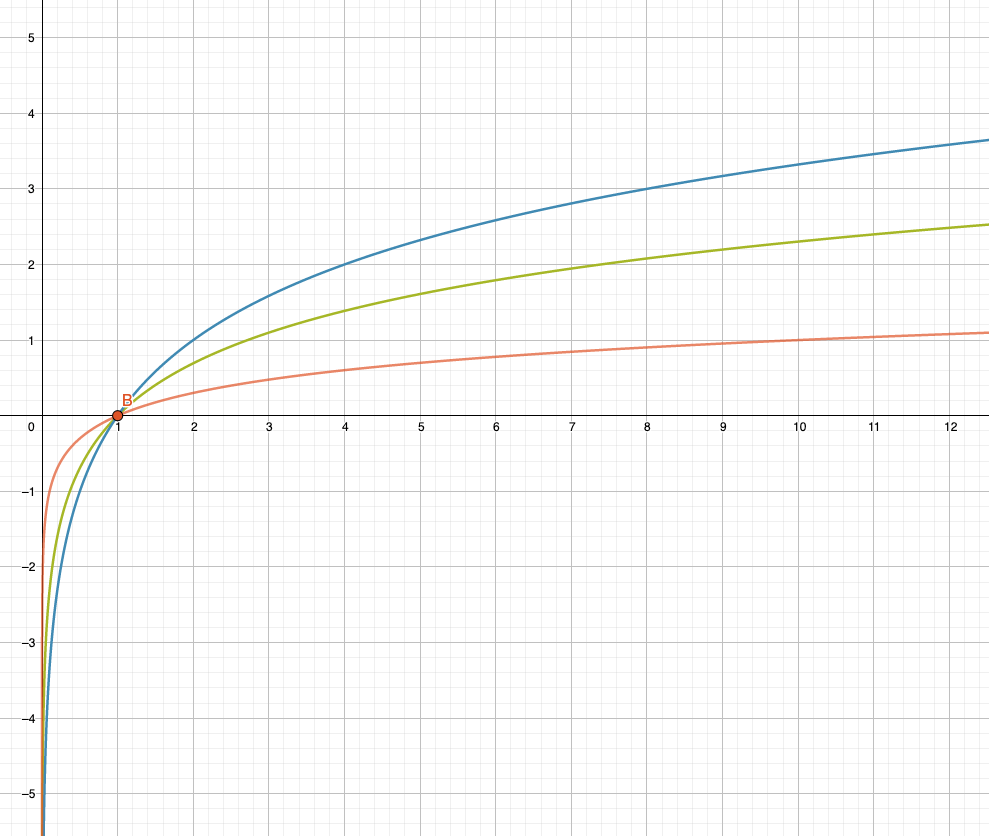
Logarithmen für Basen a<1
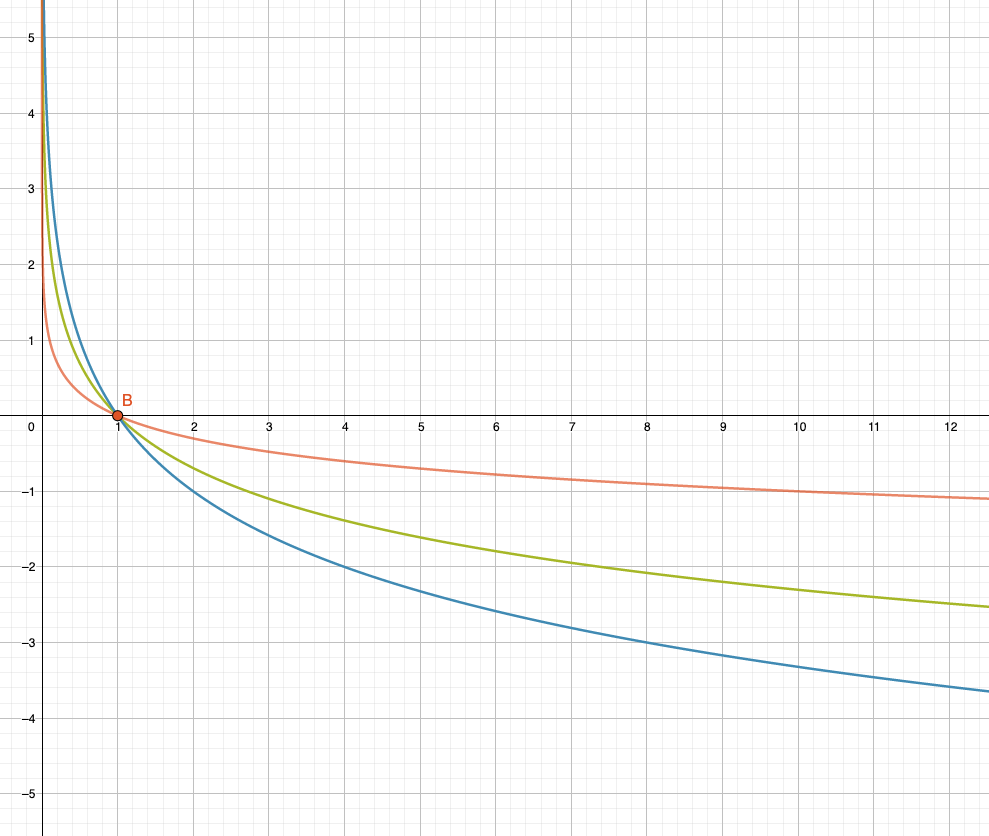
Für die Basis haben wir uns bis hierher auf \(a>1\) beschränkt, wie z.B. \(a=2\), \(a=e\) oder \(a=10\). Wie steht es mit sehr kleinen Basen aus, die zwar positiv (Bedingung!), aber kleiner als 1 sind? Wie wäre z.B. der Verlauf eines Logarithmus mit Basis \(a=\frac{1}{2}\) ?
Für diese Basis gilt beispielsweise:
\[ \log_{(1/2)}\Big( \frac{1}{2} \Big) = 1 \quad \Leftrightarrow \quad \Big( \frac{1}{2} \Big)^1 = \frac{1}{2} \]
\[ \log_{(1/2)} (2) = -1 \quad \Leftrightarrow \quad \Big( \frac{1}{2} \Big)^{-1} = \frac{1}{2^{-1}} = 2^1 = 2 \]
Ausserdem wird diese Kurve auch durch den Punkt B(1,0) gehen, der allen Logarithmen gemeinsam ist. Wir haben somit die folgenden drei Punkte, die diese Kurve ausmachen:
\[ (\frac{1}{2},1), \;\; B(1,0), \;\; (2,-1)\]
Es ist eine fallende Kurve, die von oben links oben nach unten rechts abfällt. In der folgenden Grafik ist es die blaue Kurve:
Ableitung Logarithmus
Die Ableitung der Logarithmusfunktion erhalten wir sehr einfach mit Hilfe der Ableitung einer Umkehrfunktion. Sie wird dort als Beispiel vorgerechnet. Der Logarithmus ist ja die Umkehrfunktion der Exponentialfunktion.
Erste Ableitung Logarithmusfunktion:
\[ \frac{d}{dx}\Big(\ln(x)\Big) = \frac{1}{x} \]
\[ \frac{d}{dx}\Big(\log_a(x)\Big) = \frac{1}{\ln (a) \cdot x} \]
Beispiel: Steigung in der Nullstelle
Welche Steigung hat der natürliche Logarithmus in seiner Nullstelle?
Aufgabensammlung
Lernziele
- Du weisst, wie der Logarithmus definiert ist und wie die Fragestellung heisst, mit welcher du dir die Bedeutung des Logarithmus merken solltest. Du kannst den Logarithmus in eine äquivalente Potenz umwandeln und umgekehrt.
- Du weisst, dass der Logarithmus das schwächste Wachstum überhaupt hat und somit die geringste Mächtigkeit hat, auch wenn die Logarithmusfunktion anfangs (für kleine x) unendlich steil ist.
- Du weisst, dass der Logarithmus die Umkehrfunktion der Exponentialfunktion ist.
- Du weisst, dass der Logarithmus einer Potenz (mit gleicher Basis) und die Potenz eines Logarithmus (mit gleicher Basis) sich gegenseitig aufheben und wir damit einen Logarithmus oder eine Potenz (mit Unbekannter im Exponenten) weg kriegen.
- Du kannst Exponentialgleichungen lösen, indem du den Logarithmus auf die ganze Gleichung anwendest.
- Du kannst den Verlauf der Logarithmusfunktion zu einer gegeben Basis a zeichnen.
- Du kannst die Logarithmusfunktion ableiten.
Weitere Links
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.





Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.