Exponentielle Abklingfunktion

Mit der Abklingfunktion ist ein exponentieller Zerfall gemeint, der sich einem Grenzwert nähert. Solche Verläufe über die Zeit sind in den Naturwissenschaften und in der Technik sehr verbreitet. Die Abklingfunktion kann aber auch eine Funktion des Ortes sein, z.B. wenn die Temperatur oder die Konzentration eines Stoffs mit zunehmendem Abstand abnimmt.

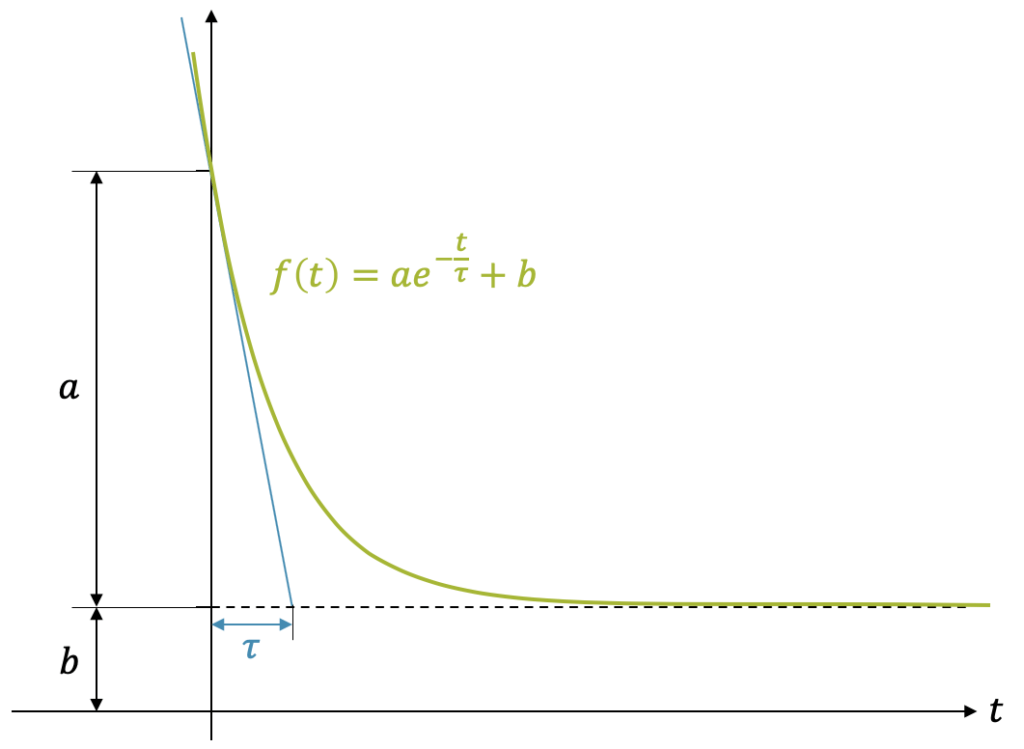
Es gibt unendlich viele Varianten von Abklingfunktionen. Mit drei Kenngrössen bzw. Informationen wird die Abklingfunktion aber fertig beschrieben:

• Funktionswert beim Start (erster Punkt bei \(t=0\))
• Grenzwert für \(t \rightarrow \infty\) oder zweiter Punkt für \(t>0\)
• Abklingrate, d.h. wie schnell das Abklingen ist

Die Zeitkonstante wird mit dem griechischen Buchstaben \(\tau\) (“tau”) definiert. Sie ist die Zeit, die verstreichen würde, wenn die Funktion linear abfallen und den Grenzwert erreichen würde (siehe Grafik). Eine andere Definition besagt, dass zum Zeitpunkt \(\tau\) der Funktionswert auf den “\)e\)-ten” Teil des Startwerts über Grenzwert gefallen ist, d.h. \(\frac{1}{e} = 0.368 \approx \frac{1}{3}\) noch etwa einen Drittel verbleibend oder um rund zwei Drittel abgeklungen. Wir können uns dem vergewissern, indem wir den Funktionswert am Anfang \(f_0=f(0)\) mit dem Funktionswert \(f_1=f(\tau)\) zum Zeitpunkt \(\tau\) vergleichen:

\[ f_0 = a \cdot e^{-\frac{0}{\tau}} + b = a \cdot 1 + b = a + b \]

\[ f_1 = a \cdot e^{-\frac{\tau}{\tau}} + b = a \cdot e^{-1} + b = \frac{a}{e} + b \]

\[ f_0 – f_1 = \big(a + b \big) – \Big(\frac{a}{e} + b \Big) = \Big(1- \frac{1}{e} \Big) \cdot a = (1-0.368) \cdot a = 0.632 \cdot a \]

Für sehr grosse Zeiten \(t \rightarrow \infty\) nähert sich die Abklingfunktion asymptotisch dem Grenzwert b an, weil die exponentielle Zerfallsfunktion ja gegen null geht:

\[ \require{cancel} \lim_{t \rightarrow \infty}\Big( a \cdot e^{-\frac{t}{\tau}} + b \Big) = a \cdot \cancel{\lim_{t \rightarrow \infty}\Big( e^{-\frac{t}{\tau}} \Big)} + b = 0 + b = b \]