Geometrische Reihen (GR)

Endliche geometrische Reihe

Addieren wir laufend die Glieder einer geometrischen Folge, so erhalten wir eine geometrische Reihe.

Eine geometrische Folge ist entweder in der rekursiven Definition…

\[ a_n = a_{n-1} \cdot q\]

…oder in der expliziten Definition gegeben:

\[ a_n = a_1 \cdot q^{n-1} \]

Auf jeden Fall brauchen wir das Anfangsglied \(a_1\) (oder ein anderes) und den Faktor \(q\), mit welchem von einem Glied zum nächsten multipliziert wird.

Die geometrische Reihe ist die laufende Summe aller Folgeglieder \(a_k\) für die Positionen \(k=1\) bis \(k=n\):

\[ s_n = \sum_{k=1}^n a_k \]

Für die endliche geometrische Reihe gilt:

\[ s_n = a_1 \cdot \frac{q^n – 1}{q – 1} \]

Beachte dabei, dass \(q \neq 1\), da wir sonst durch null dividieren würden. Die Herleitung dieser Formel folgt weiter unten.

Im nachfolgenden Beispiel vergewissern wir uns zuerst, dass es sich um eine geometrische Folge handelt, bestimmen \(a_1\) und \(q\) und berechnen dann das Resultat mit Hilfe der Formel für die geometrische Reihe.

Herleitung

Wir betrachten als erstes die ausgeschriebene Summe für \(s_n\):

\[ s_n = a_1 + a_2 + a_3 + … + a_n \]

Jetzt ersetzen wir jedes Glied der geometrischen Folge \(a_i\) mit der expliziten Definition \(a_i = a_1 \cdot q^{(i-1)}\):

\[ s_n = a_1 + (a_1 \cdot q) +  (a_1 \cdot q^2) + … + (a_1 \cdot q^{(n-1)}) \]

Wir klammern \(a_1\) aus und erhalten:

\[ s_n = a_1 \cdot (1 + q + q^2 + … + q^{(n-1)}) \]

Jetzt multiplizieren wir die ganze Gleichung mit \(q\), wobei wir auf der rechten Seite die Klammer mit \(q\) ausmultiplizieren:

\[ q \cdot s_n = a_1 \cdot (q + q^2 + q^3 + … + q^{n}) \]

Dann bilden wir die Differenz \(s_n – q \cdot s_n\) der beiden vorigen Gleichungen:

\[ a_1 \cdot (1 + q + q^2 + … + q^{(n-1)}) \;\;-\;\; a_1 \cdot (q + q^2 + q^3 + … + q^{n}) \]

Links wird \(s_n\) ausgeklammert. Rechts packen wir die beiden Klammern zu einer zusammen:

\[ \require{cancel} a_1 \cdot (1 + \cancel{q} + \cancel{q^2} + \cancel{q^3} + … + \cancel{q^{(n-1)}} – \cancel{q} – \cancel{q^2} – \cancel{q^3} – … – \cancel{q^{(n-1)}}- q^{n}) \]

Die meisten Terme in der Klammer heben sich gegenseitig auf. Wir finden ein \(q\), aber auch ein \(-q\), dann gibt es ein \(q^2\), das vom \(-q^2\) aufgehoben wird etc. Übrig bleibt nur der erste (\(+1\)) und der letzte Term (\(-q^n\)):

\[ s_n \cdot (1- q) = a_1 \cdot (1 – q^{n}) \]

Wenn wir die Gleichung mit \((-1)\) multiplizieren, erhalten wir

\[ s_n \cdot (q- 1) = a_1 \cdot (q^{n} – 1) \]

Schliesslich dividieren wir durch \((q-1)\), wobei wir einschränken, dass das nur für \(q \neq 1\) gilt:

\[ s_n = a_1 \cdot \frac{q^{n} – 1}{q-1} \]

Unendliche geometrische Reihe

Die unendliche geometrische Reihe ist von besonderem Interesse, denn wir bilden eine Summe mit unendlich vielen Summanden und in den interessanten Fällen bleibt die Summe endlich!

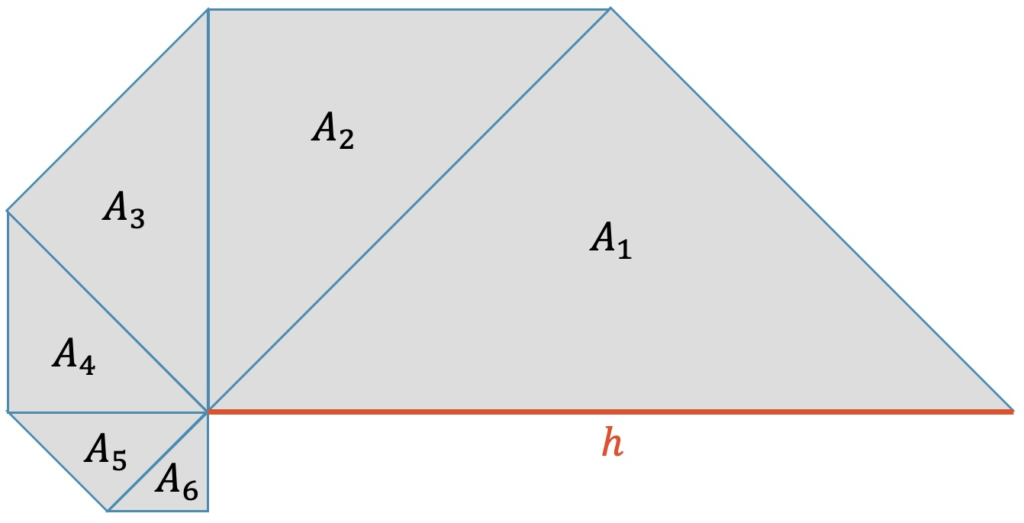
Schau dir die untenstehende Figur an. Wir beginnen mit einem ”L”, das \(\frac{3}{4}\) eines Quadrats entspricht. Dann legen wir ein genau halb so grosses ”L” hinein.

Da die Seiten des zweiten “L” halb so gross sind, ist die Fläche nur noch ein Viertel des ersten “L”.

Wie du siehst, ist mit 6 solchen ”L” schon fast die ganze Quadratfläche ausgefüllt. Natürlich bleibt immer ein kleines Stückchen oben rechts, das noch nicht ausgefüllt ist.

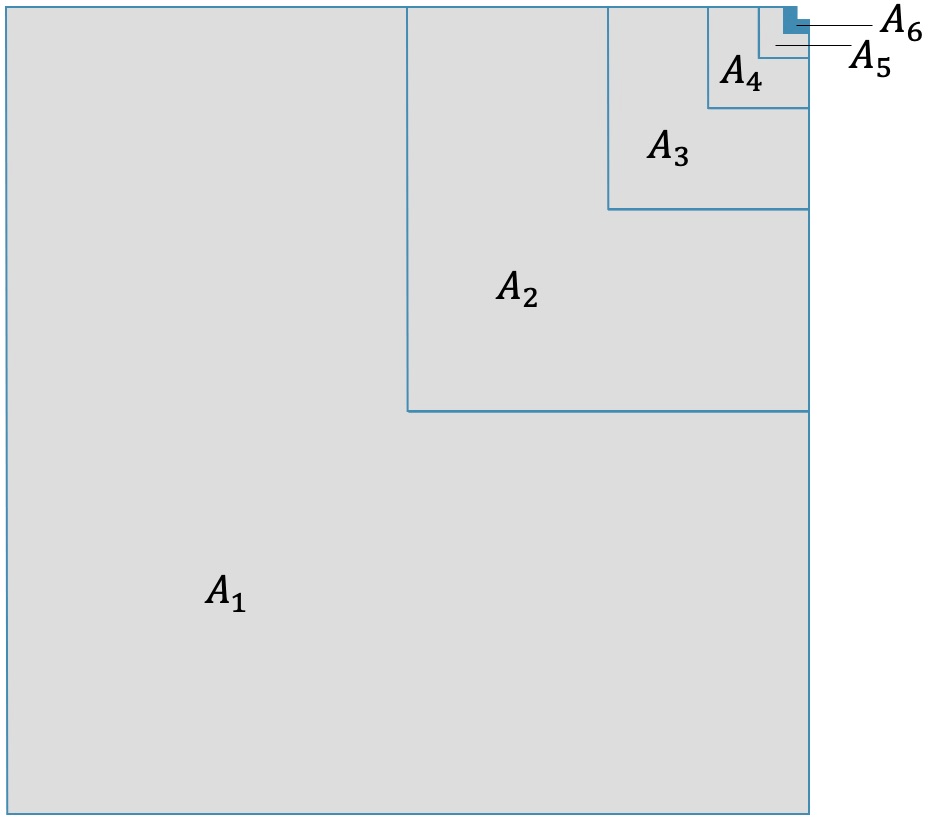
Was passiert, wenn wir bei \(A_6\) nicht stoppen, sondern bis ins Unendliche gehen, d.h. bis \(A_\infty\)?

\[ A = A_1 + A_2 + A_3 + … + A_\infty \]

Das gibt natürlich die Fläche des Quadrats. Sie ist definitiv nicht unendlich, kann aber als Summe mit unendlich vielen Summanden berechnen!

Angenommen, du realisierst ein solches Quadrat als Kunstwerk in einer Grösse von 1 m x 1 m und du bemalst alle ”L’-Flächen’ mit unterschiedlichen Farben. Obwohl es unendlich viele Flächen sind und du gar nie fertig sein kannst mit malen, brauchst du nur Farbe für einen Quadratmeter Fläche!

Der Grund für dieses scheinbare Paradoxon liegt natürlich darin, dass die Summanden in der Summe immer kleiner werden. Das werden sie aber nur, wenn in der geometrischen Folge \(|q|<1\) gilt.

Wir können die unendliche geometrische Reihe \(s_\infty\) berechnen mit der folgenden einfachen Formel. Beachte, dass wir auch hier nur den Startwert \(a_1\) und den Faktor \(q\) brauchen:

\[ s_\infty = \frac{a_1}{1-q} \]

Für unser Quadrat mit Seitenlänge \(s\) gilt:

\[ A_1 = \frac{3}{4}s^2 \qquad q=\frac{1}{4} \]

somit erhalten wir für \(s_\infty\):

\[ s_\infty = \frac{\frac{3}{4}s^2}{1-\frac{1}{4}} = \frac{\Big(\frac{3}{4}\Big)}{\Big(\frac{3}{4}\Big)} \cdot s^2 = s^2 \]

Die Rechnung bestätigt, dass wir im Unendlichen das ganze Quadrat mit der Fläche \(s^2\) erhalten würden!

Herleitung

\[ s_\infty = \lim_{n \to \infty} s_n = \lim_{n \to \infty} \Big( a_1 \cdot \frac{q^{n} – 1}{q-1} \Big) \]

Den Faktor \(a_1\) können wir aus dem limes ausklammern, da er ja konstant ist und von \(n\) nicht abhängt:

\[ s_\infty = a_1 \cdot \lim_{n \to \infty} \Big(\frac{q^{n} – 1}{q-1} \Big) \]

\[ s_\infty = a_1 \cdot \frac{\lim\big(q^{n}\big) – \lim(1)}{\lim(q-1)} \]

Der einzige limes, der noch Sinn macht, ist derjenige mit \(q^n\). Die anderen sind limes von Konstanten, die so oder so gleich bleiben, unabhängig von \(n\). Deshalb:

\[ s_\infty = a_1 \cdot \frac{\lim\big(q^{n}\big) – 1}{q-1} \]

Jetzt schauen wir uns \(\lim_{n \rightarrow \infty} \big( q^n \big)\) an. Wir erinnern uns daran, dass gewisse Potenzen kleiner werden, je grösser der Exponent ist, z.B.

\[ \Big(\frac{1}{2}\Big) > \Big( \frac{1}{2} \Big)^2 > \Big( \frac{1}{2} \Big)^3 > \Big( \frac{1}{2} \Big)^4 \]

Für \(|q|<1\) gilt das auch!

\[ q > q^2 > q^3 > q^4 > … > q^n \]

Somit wird uns klar, dass wenn \(n \rightarrow \infty\) wir mit dem Wert der Potenz von \(|q| < 1\) gegen null gehen:

\[ \lim_{n \rightarrow \infty} \big( q^n \big) = 0 \]

Damit erhalten wir für die unendliche Summe:

\[ s_\infty = a_1 \cdot \frac{0 – 1}{q-1} \]

Wir erweitern den Bruch mit (-1) und erhalten so die Formel für die unendliche geometrische Reihe:

\[ s_\infty = \frac{a_1}{1-q} \]

Achilles und die Schildkröte

Der griechische Philosoph Zenon von Elea hat ca. 500 Jahre vor Christus gelebt. Es wird vermutet, dass das Paradoxon von Achilles und der Schildkröte von ihm beschrieben wurde.

Achilles, der beinahe unverwundbare Held soll ein Wettrennen mit einer Schildkröte antreten. Damit die offensichtlich langsamere Schildkröte eine Chance hat, erhält sie einen Vorsprung, sagen wir mal 100 m.

Beide starten gleichzeitig. Nachdem Achilles die 100 m Vorsprung geschafft hat, ist die Schildkröte natürlich auch schon ein Stück weiter, sagen wir mal 50 m (Das ist in unserem Zahlenbeispiel natürlich eine besonders schnelle Schildkröte mit Superkräften, so dass sie halb so schnell laufen kann wie Achilles!).

In der Zeit, in welcher Achilles nun auch diesen verbleibenden Vorsprung von 50 m hinter sich bringt, hat die Schildkröte wieder einen kleinen Vorsprung geschafft usw.

Achilles wird es anscheinend nie schaffen, die Schildkröte einzuholen, obwohl er schneller läuft als die Schildkröte!

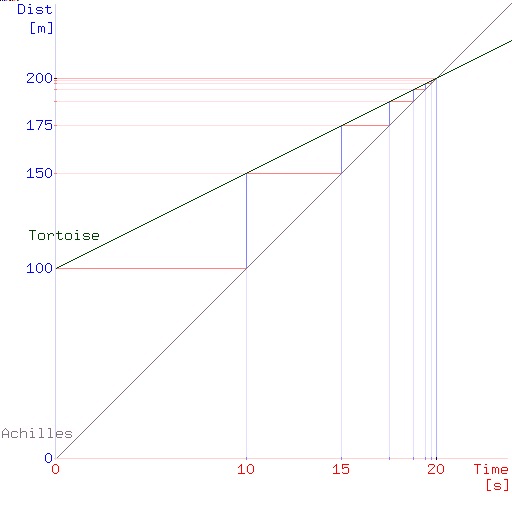
Zeit	0	10 s	15 s	17.5 s	…
Achilles	0	100 m	150 m	175 m	…
Schildkröte	100 m	150m	175 m	187.5 m	…
Abstand	100 m	50 m	25 m	12.5 m	…

Wenn wir uns den Abstand zwischen den beiden anschauen, so entspricht er einer geometrischen Folge mit Faktor \(q=\frac{1}{2}\) und Startwert \(a_1\) = 100 m.

Die geometrische Reihe entspricht der Summe aller Abstände und die unendliche Summe ist die maximale Distanz, die Achilles zurücklegen muss, um die Schildkröte zu überholen.

Da \(|q|<1\) gilt, können wir diese unendliche Summe bilden und ihr Betrag ist endlich. Man sagt auch, die geometrische Reihe konvergiert.

Das heisst aber auch, dass Achilles eine endliche Strecke zurücklegen muss, bis er die Schildkröte eingeholt hat.

Wir können diese Strecke berechnen mit der Formel für die unendliche geometrische Reihe:

\[ s_\infty = \frac{a_1}{1-q} = \frac{100}{1-0.5} = \frac{100}{0.5} = 200 \]

Nach unseren Berechnungen muss Achilles 200 m rennen und hat dann die schnelle Schildkröte erreicht.

Das Gleiche erhalten wir auch, wenn wir die Aufgabe grafisch lösen. Nach 200 m kreuzt Achilles die Schildkröte.

Wo ist jetzt das Paradoxon geblieben?

Es entstand eigentlich nur, weil wir einen immer kürzeren Zeitabschnitt betrachteten haben, also ein bisschen wie wenn wir den Film immer langsamer laufen lassen würden.

In so einem Fall holt Achilles die Schildkröte wirklich nie ein.