Fermat’sches Prinzip

Konstruktive und destruktive Interferenz

In der Welt der Wellen füllt die Welle den “Raum” aus, der ihr zur Verfügung steht. Da Licht sich wie eine Welle verhält, heisst das: Die Strahlen nehmen alle möglichen Wege ein, nicht nur den kürzesten und geraden Weg.

Eine weitere Welleneigenschaft ist, dass Wellen sich konstruktiv oder destruktiv überlagern können (Interferenz), d.h. sie können sich selber verstärken oder auslöschen.

Wellen überlagern ideal konstruktiv, wenn ihre Phase null ist, d.h. wenn Wellenberge auf Wellenberge und Wellentäler auf Wellentäler treffen.

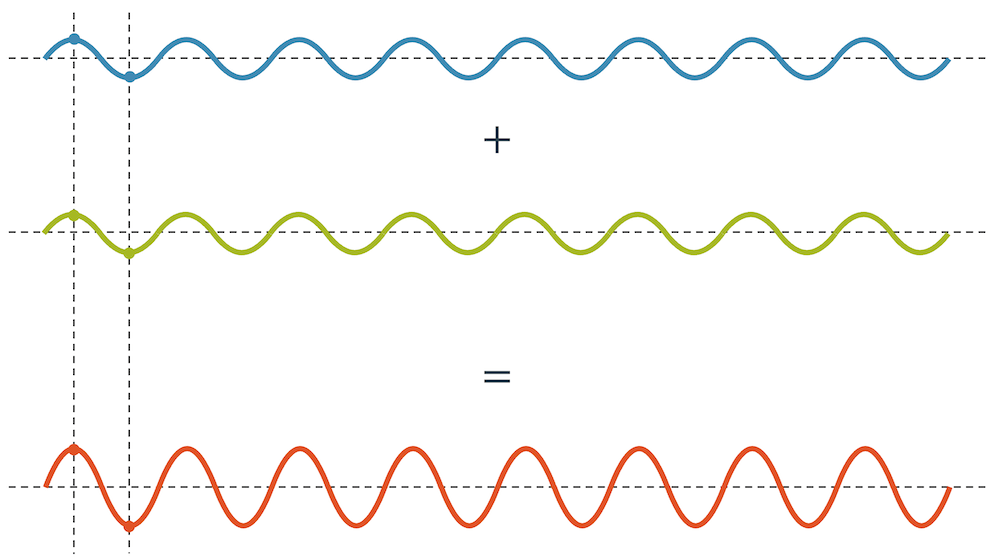
Die ideale und vollständige Auslöschung haben wir, wenn die Wellenberge genau auf Wellentäler treffen, d.h. wenn die Phase so ist, dass die beiden Wellen genau um eine halbe Wellenlänge versetzt sind.

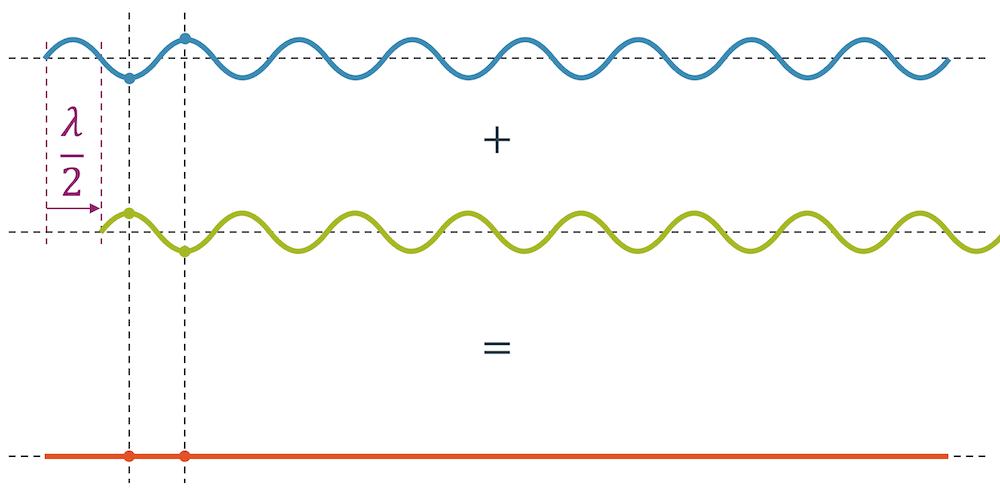
Wenn wir Wellen haben, die den ganzen Raum ausfüllen, werden wir alle erdenkbaren Kombinationen von Phasen vorfinden. Wenn ich irgendeine Welle nehme, dann werde ich in der grossen Vielzahl von verfügbaren Wellen eigentlich immer das Gegenstück finden, das meine erste Welle genau auslöscht.

Wenn wir alle Wellen überlagern, werden sie destruktiv interferieren und sich alle auslöschen.

Um dies zu illustrieren, machen wir ein kleines Beispiel: Auf der Uhr ist die Zahl 12 gegenüber der Zahl 6, die Zahl 1 ist gegenüber der Zahl 7 etc. Diese Zeiten sollen unsere Wellen darstellen.

Wenn wir alle möglichen ganzen Stunden nehmen, haben wir folgende Zahlenmenge:

\[ \{ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 \} \]

Jetzt überlagern wir unsere “Wellen” und bilden sechs Pärchen, die sich gegenseitig auslöschen:

\[ \Big \{ (1,7), \; (2,8), \; (3,9), \; (4,10), \; (5,11), \; (6,12) \Big \} \]

Wir sollten an dieser Stelle überzeugt sein, dass eine ganz zufällige Menge an Wellen sich auslöschen würden. 😎

Nehmen wir jetzt folgende Zahlenmenge:

\[ \{ 1, 1.5, 2, 2.5, 3, 4, 6, 7, 9, 10, 11, 12 \} \]

Auf den ersten Blick haben wieder eine unübersichtliche Zahlenmenge. Dieses Mal löschen sich aber nicht alle “Wellen” aus. Es fällt auch auf, dass es überdurchschnittlich viele Zahlen in der Umgebung der 2 hat. Diese 2, die 1.5 und 2.5 haben auch kein “Gegenstück”. Es fehlen uns die 7.5, die 8 und die 8.5. Die anderen Zahlen werden verschwinden, aber um die 2 herum werden die “Wellen” übrig bleiben.

Ein bisschen so müssen wir uns Fermat’s Prinzip vorstellen: Wir finden das Grüppchen von Wellen, die zahlreicher sind und kein “Gegenstück” haben, das sie auslöschen wird.

Fermat’sches Prinzip und extremaler Weg

Das Fermat’sche Prinzip ist nach dem französischen Mathematiker Pierre de Fermat (1607-1665) benannt. Es besagt, dass Wellen den Weg einnehmen werden, dessen Laufzeit extremal, d.h. minimal oder maximal ist.

Wenn wir die Funktionswerte der Funktion in der Nähe des Minimums notieren würden, könnte das in etwa so aussehen:

\[ \{ …, 6, 4, 3, 2.5, 2.1, \;2\;, 2.1, 2.5, 3, 4, … \} \]

Um das Minimum herum – sagen wir mal es betrage 2 – häufen sich die Funktionswerte, die sehr ähnlich sind. Weiter weg davon sind sie sehr unterschiedlich.

Die Welle mit dem kürzesten Weg hat deshalb Nachbarwellen, die nur ganz unwesentlich abweichen. Der kürzeste Weg ist ein Minimum und links und rechts von einem Minimum bleibt die Funktion praktisch konstant. Die Steigung im Minimum ist sogar null!

Wenn wir in der Nähe eines Minimums viele Wellen haben, die fast gleich sind, werden sie sich gegenseitig verstärken, während die übrigen, ganz unterschiedlichen Wellen sich gegenseitig auslöschen werden. Das “Grüppchen” von Wellen beim Minimum wird übrig bleiben.

Beim Maximum verhält es sich genau gleich. Bei kleinen Abweichungen vom Maximum haben wir viele Wellen, die sich gegenseitig verstärken, weil sie praktisch gleich sind. Jetzt ist ein maximaler Weg aber kaum bestimmbar, denn man kann einen Weg immer noch länger machen. Wir beschränken uns deshalb auf den zeitlich kürzesten Weg: das Minimum.

Nach dem Fermat’schen Prinzip löschen sich (fast) alle Wellen aus. Nur die Wellen, die den zeitlich minimalen Weg eingenommen haben, bleiben bestehen. Wir sehen sie als Lichtstrahlen.

Reflexionsgesetz

Wir können das Reflexionsgesetz mit Fermat’s Prinzip geometrisch beweisen: Vom virtuellen Spiegelbild zum Beobachter ist der kürzeste Weg die gerade Linie. Sie schneidet die Spiegelebene in einem bestimmten Punkt. Genau dort trifft der Lichtstrahl auf, bevor er mit gleichem Winkel reflektiert wird.

Würden wir einen anderen Punkt auf dem Spiegel wählen, würde die Verbindung vom virtuellen Bild zum Beobachter einen Knick aufweisen und wäre damit nicht minimal!

Mit der obigen Konstruktion erhalten wir zwei spiegelsymmetrische Dreiecke mit gleichen Winkeln. Ausserdem ist die Hypotenuse der beiden Dreiecke gleich lang, d.h. der effektive Weg des Lichtstrahls ist genau gleich lang, wie die gerade Linie vom virtuellen Bild zum Beobachter. Somit ist der Strahlengang ebenfalls minimal!

Damit entspricht der Weg eines Lichtstrahls, der an einem Spiegel reflektiert wird, dem kürzest möglichen Weg, gemäss Fermat’s Prinzip. Jede Abweichung davon würde einem längeren Weg entspricht.

Brechungsgesetz

Beim Brechungsgesetz geht es auch darum den kürzesten Weg zu finden. Wir benutzen dazu die Analogie mit dem Strandwächter, der eine Person in Not retten möchte.

Die gerade Linie ist hier nicht die Lösung, denn im Wasser ist der Strandwächter langsamer als auf dem Sand. Es ist deshalb von Vorteil, den Weg auf dem Sand etwas zu verlängern und dafür den Weg im Wasser etwas zu verkürzen.

Sobald wir die gerade Linie verlassen, wird der Weg insgesamt etwas länger. Unser Ziel ist es aber, den zeitlich kürzesten Weg zu finden. Wir nehmen ein paar Meter Sand in Kauf, solange wir damit ein paar Meter im Wasser einsparen können. Der Weg wird zwar etwas länger, aber wir sparen Zeit. ⌛️

Weil jetzt die Geschwindigkeit und damit die auch die Zeit eine Rolle spielt, können wir das Brechungsgesetz nicht mehr rein geometrisch beweisen. Wir werden dazu die Differenzialrechnung benutzen.

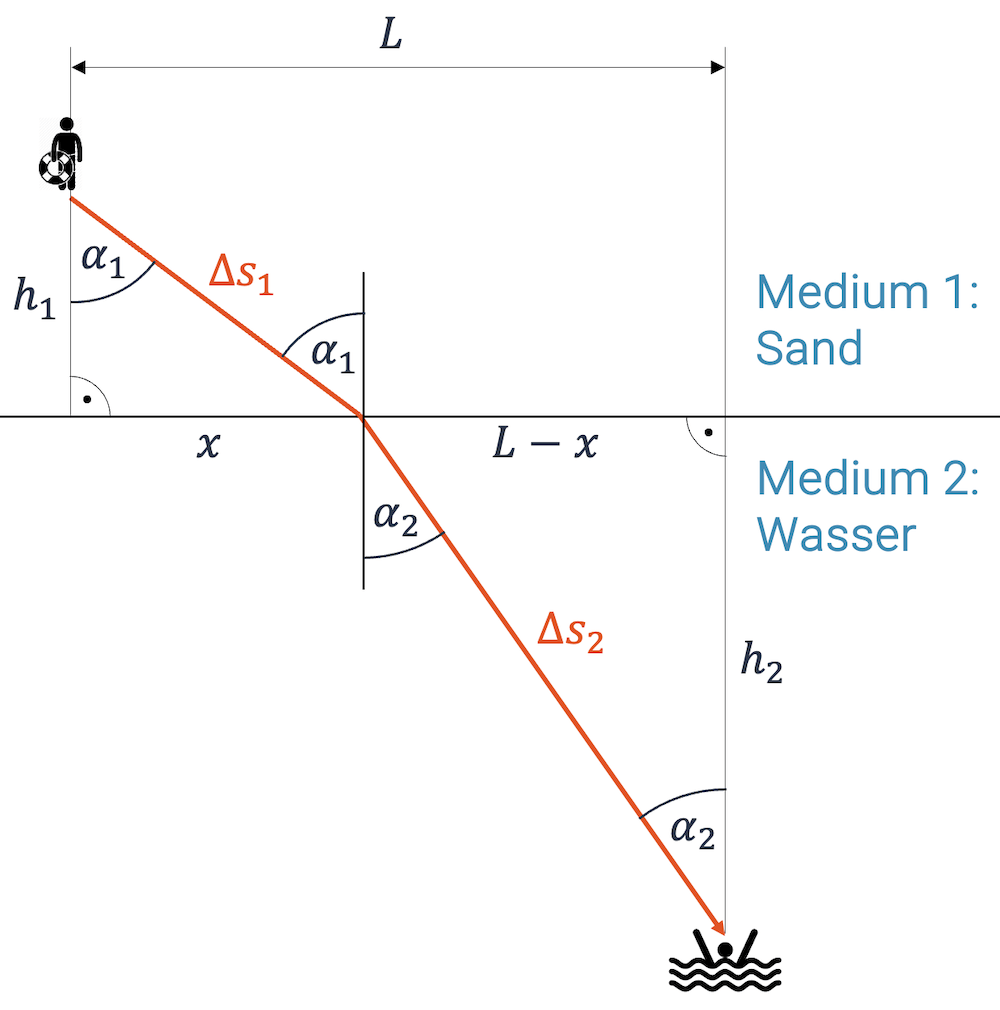
Der totale Weg, den der Lichtstrahl absolviert, ist \(\Delta s_1 + \Delta s_2 \). Die Zeit die es dazu braucht, ist:

\[ \Delta t_1 + \Delta t_2 \;\; = \;\; \frac{\Delta s_1}{u_1} + \frac{\Delta s_2}{u_2} \]

Die Geschwindigkeit des Strandwächters auf Sand ist \(u_1\) und im Wasser ist \(u_2\). Beim Licht benutzen wir die Brechungsindizes als Faktoren der Verlangsamung gegenüber der maximalen Lichtgeschwindigkeit im Vakuum \(c_0\):

\[ u_1 = \frac{c_0}{n_1}, \qquad u_2 = \frac{c_0}{n_2} \]

Wir setzen das in die totale Zeit \(\Delta t_{\text{tot}}\)ein und erhalten:

\[ \Delta t_{\text{tot}} = \frac{\Delta s_1 \cdot n_1}{c_0} + \frac{\Delta s_2 \cdot n_2}{c_0} \]

\[ \Delta t_{\text{tot}} = \frac{1}{c_0} \cdot \Big(\Delta s_1 \cdot n_1 + \Delta s_2 \cdot n_2 \Big) \]

Jetzt ersetzen wir die Streckenstücke \(\Delta s_1\) und \(\Delta s_2\) mit Hilfe des Satzes von Pythagoras:

\[ \Delta s_1 = \sqrt{x^2 + h_1^2}, \qquad \Delta s_2 = \sqrt{(L-x)^2 + h_2^2} \]

Oben eingesetzt ergibt das:

\[ \Delta t_{\text{tot}}(x) = \frac{1}{c_0} \cdot \Big(\sqrt{x^2 + h_1^2} \cdot n_1 + \sqrt{(L-x)^2 + h_2^2} \cdot n_2 \Big) \]

Jetzt haben wir die totale Zeit \(\Delta t_{\text{tot}}(x)\) als Funktion, abhängig vom Brechungspunkt, den wir mit der Variablen \(x\) definiert haben. Wir können jetzt nach dem Minimum suchen, indem wir mit der Differenzialrechnung die erste Ableitung unserer Funktion bestimmen. Beachte, dass wir aufgrund der inneren Ableitung (Kettenregel) wir ein Minuszeichen erhalten:

\[ \frac{d}{dx} \Delta t_{\text{tot}} = \frac{1}{c_0} \cdot \Bigg(\frac{x \cdot n_1}{\sqrt{x^2 + h_1^2}} \;-\; \frac{(L-x)\cdot n_2}{\sqrt{(L-x)^2 + h_2^2}} \Bigg) \]

Jetzt können wir die erste Ableitung null setzen:

\[ \frac{1}{c_0} \cdot \Bigg(\frac{x \cdot n_1}{\sqrt{x^2 + h_1^2}} \;-\; \frac{(L-x)\cdot n_2}{\sqrt{(L-x)^2 + h_2^2}} \Bigg) \;\; \stackrel{!}{=} \;\; 0 \]

\[ \frac{x \cdot n_1}{\sqrt{x^2 + h_1^2}} \;\;=\;\; \frac{(L-x)\cdot n_2}{\sqrt{(L-x)^2 + h_2^2}} \]

Weil wir die Ableitung nach \(x\) hinter uns haben, brauchen wir die Wurzeln nicht mehr. Wir setzen sie wieder zurück:

\[ \frac{x \cdot n_1}{\Delta s_1} \;\;=\;\; \frac{(L-x)\cdot n_2}{\Delta s_2} \]

Jetzt nehmen wir die Definition der Sinus-Funktion als “Gegenkathete durch Hypotenuse” und können damit den \(\sin(\alpha_1)\) und den \(\sin(\alpha_2)\) aufstellen:

\[ \sin(\alpha_1) = \frac{x}{\Delta s_1}, \qquad \sin(\alpha_2) = \frac{(L-x)}{\Delta s_2} \]

In unsere Gleichung eingesetzt, erhalten wir:

\[ \sin(\alpha_1) \cdot n_1 \;\;=\;\; \sin(\alpha_2) \cdot n_2 \]

\[ \frac{\sin(\alpha_1)}{\sin(\alpha_2)} = \frac{n_2}{n_1} \]

Damit haben wir das Brechungsgesetz von Snellius gefunden.