Inhalt
Das Wichtigste in Kürze
Die Totalreflexion ist ein Wellenphänomen. Wenn der Lichtstrahl in einem Medium mit grösserem Brechungsindex relativ flach, d.h. mit einem grossen Einfallswinkel zum Lot der äusseren Grenzfläche des Mediums auftrifft, vermag der Strahl nicht aus dem Medium auszutreten und reflektiert total gemäss dem Reflexiongesetz.
Die Totalreflexion findet statt, wenn der Einfallswinkel grösser als ein bestimmter kritischer Wert \(\alpha_{TR}\) ist. Ist der Einfallswinkel unterhalb dieses kritischen Werts, findet normale Brechung statt, d.h. der Strahl tritt aus dem Medium aus und wird dabei gebrochen.
Der kritische Wert \(\alpha_{TR}\) kann mit Hilfe der folgenden Formel berechnet werden. Er ist von beiden Brechungsindizes abhängig:
\[ \alpha_{TR} = \arcsin \Big( \frac{n_2}{n_1} \Big) \]
Dabei ist \(n_1\) der grössere Brechungsindex des optisch dichteren Mediums mit langsamerer Lichtgeschwindigkeit und \(n_2\) der kleinere Brechungsindex, z.B. von der umgebenden Luft.
Tutorial Videos
(Es gibt leider keine Tutorial Videos zu diesem Thema)
Bedeutung des kritischen Winkels
Die Totalreflexion ist ein typisches Wellenphänomen, das v.a. bei Licht ausgenutzt wird. Wenn der Lichtstrahl in einem optisch dichteren Medium (mit grösserem Brechungsindex) relativ flach, d.h. mit einem grossen Einfallswinkel auf die äussere Grenzfläche auftrifft, so vermag er nicht aus dem Medium auszutreten und reflektiert total im Medium gemäss dem Reflexiongesetz.
Warum es zur Totalreflexion kommt, erkennen wir in der nachfolgenden Grafik:

Links haben wir den normalen Fall von Brechung. Der Strahl bricht mit einem grösseren Brechungswinkel, weil das obere Medium einen kleineren Brechungsindex hat (und das Licht dort schneller ist).
Wenn wir uns jetzt vorstellen, dass wir den Einfallswinkel \(\alpha_1\) noch etwas vergrössern, dann erreichen wir irgendwann einen Brechungswinkel von 90°, d.h. der Lichtstrahl kommt gar nicht mehr richtig aus dem Medium 1 heraus.
Der Einfallswinkel, der zu dieser kritischen Situation führt, nennen wir ab jetzt kritischen Winkel \(\alpha_{TR}\). Er wird auch Grenzwinkel der Totalreflexion genannt:
- \(\alpha_1 < \alpha_{TR}\) Der Einfallswinkel ist unter dem kritischen Wert, es folgt Brechung gemäss Brechungsgesetz.
- \(\alpha_1 = \alpha_{TR}\) Der Einfallswinkel hat den kritischen Wert erreicht und wird im Prinzip gerade noch gebrochen, jedoch tritt der Strahl nicht mehr richtig aus dem Medium 1 heraus (Grenzfall)
- \(\alpha_1 > \alpha_{TR}\) Der Einfallswinkel ist über dem kritischen Wert, was zu Totalreflexion führt, mit Reflexionsgesetz.
In einem Medium mit grösserem Brechungsindex (als die Umgebung) kann Totalreflexion entstehen, wenn der Einfallswinkel grösser als der kritische Wert \(\alpha_{TR}\) ist. Dieser kritische Wert hängt von den beiden Brechungsindizes ab.
“Das Erstaunliche ist, dass Licht im transparenten Wasser, an der Grenze zur ebenfalls transparenten Luft vollständig reflektiert wird, als wäre dort ein idealer Spiegel!”
Im Medium mit kleinerem Brechungsindex (im Vergleich zur Umgebung) ist keine Totalreflexion möglich, d.h. wir können z.B. Totalreflexion haben in Wasser gegenüber Luft, jedoch nicht in Luft gegenüber Wasser.

Das obige Experiment zeigt uns, wie Lichtstrahlen in einem Bereich über der Lichtquelle aus dem Wasser austreten (Brechung). Ein Teil der Strahlen wird jedoch totalreflektiert, weil der Einfallswinkel den kritischen Winkel \(\alpha_{TR}\) überschritten hat.
Das Erstaunliche ist, dass der zweite Beobachter (rechts) das Licht gar nicht sehen kann, weil es nicht aus dem Wasser austritt. Dass Licht im transparenten Wasser, an der Grenze zur ebenfalls transparenten Luft vollständig reflektiert wird, als wäre dort ein idealer Spiegel ist schon überraschend! 😮
Berechnung des kritischen Winkels
Totalreflexion entsteht, sobald der Einfallswinkel \(\alpha\) den kritischen Winkel \(\alpha_{TR}\) überschreitet. Der kritische Winkel wird mit Hilfe der beiden Brechungsindizes berechnet, d.h. dem Brechungsindex des Mediums 1 in welchem der Strahl sich befindet und dem Medium 2, welches das Medium 1 umgibt.
Totalreflexion im Medium 1 tritt ein bei \(n_1 > n_2\) und \(\alpha_1 > \alpha_{TR}\)
Der kritische Winkel \(\alpha_{TR}\)wird wie folgt berechnet:
\[ \alpha_{TR} = \arcsin \Big( \frac{n_2}{n_1} \Big) \]
Beispiel

Herleitung
Im kritischen Fall hat der Einfallswinkel den kritischen Wert \(\alpha_1 = \alpha_{TR}\) und der Brechungswinkel beträgt \(\alpha_2 = 90^\circ\). Wir setzen für diesen Fall das Brechungsgesetz an:
\[ \frac{\sin(\alpha_1)}{\sin(\alpha_2)} = \frac{\sin(\alpha_{TR})}{\sin(90^\circ)} = \frac{n_2}{n_1} \]
Nun wissen wir, dass \(\sin(90^\circ)=1\). Wir erhalten deshalb:
\[ \sin(\alpha_{TR}) = \frac{n_2}{n_1} \]
Schliesslich setzen wir die Gleichung beidseitig in die Arkussinus-Funktion ein. Wir wissen, dass damit der Sinus auf der linken Seite verschwinden wird:
\[ \arcsin\big(\sin(\alpha_{TR})\big) = \arcsin\Big( \frac{n_2}{n_1} \Big) \]
So erhalten wir die Formel für den kritischen Winkel \(\alpha_{TR}\):
\[ \alpha_{TR} = \arcsin\Big( \frac{n_2}{n_1} \Big) \]
Anwendungen der Totalreflexion
Der Anteil des Internetverkehrs, der über Glasfaser abgewickelt wird, beträgt in der Schweiz oder in Deutschland rund 30% – Tendenz steigend. Im interkontinentalen Datenverkehr werden auch Glasfasern eingesetzt.
Glasfasern nutzen Totalreflexion aus, denn das Licht, als Träger der Information, reflektiert an den Innenwänden der Glasfaser und pflanzt sich so über weite Distanzen fort.

In der nachfolgenden Grafik ist dargestellt, wie wir uns den Weg des Lichtsignals in der Faser vorstellen können. Interessanterweise braucht die Innenseite der Faser nicht speziell reflektierend gemacht zu werden, noch ist ein Abschirmen nötig. Der Umstand, dass um die Faser herum Luft ist, mit einem kleineren Brechungsindex, reicht aus.

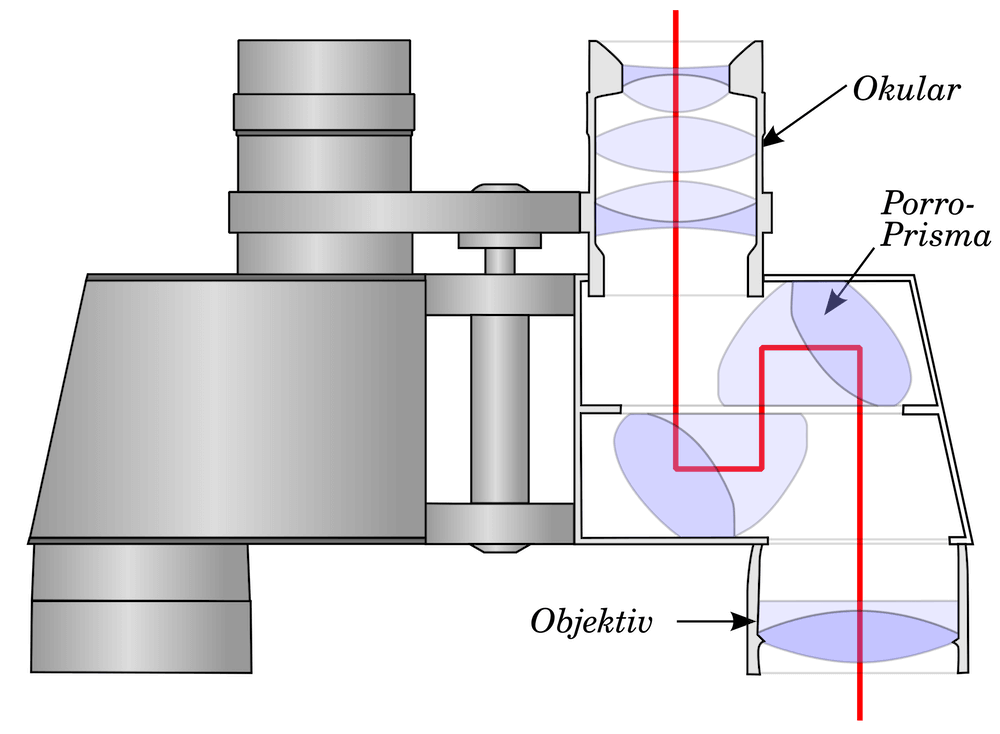
Eine andere Anwendung der Totalreflexion ist der Einsatz von Prismen in optischen Geräten. Der Feldstecher (Fernglas) hat zwei Prismen eingebaut, die mit Totalreflexion arbeiten. Die kompliziert anmutende Umlenkung von Strahlen ist nötig, da das Teleskop ein umgekehrtes Bild erzeugt. Mit dem Prismenpaar wird dieses Bild wieder umgekehrt.
Weitere Videos
Aufgabensammlung
Lernziele
Mini-Test
Um Zugang zum Mini-Test zu kriegen,
musst du vollwertiges Mitglied im Hacker-Club sein.
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt








Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.