Konkavspiegel (Hohlspiegel)

Der Konkavspiegel bzw. Hohlspiegel hält ein paar interessante Überraschungen bereit, weil er fast alles kann:

• Vergrösserte oder verkleinerte Bilder
• Virtuelle oder reelle Bilder
• Aufrechte oder umgekehrte Bilder

Der Konkavspiegel ähnelt damit der Sammellinse, die auch diese verschiedenen Arten von Bilder erzeugen kann.

Im weiteren werden wir sehen, wie diese Bilder mit Hilfe von speziellen Strahlen und deren Schnittpunkten (Bildpunkte) konstruiert werden können.

Optische Achse und Parallelstrahlen

Die optische Achse ist die Linie, die horizontal von links nach rechts gezeichnet wird. Der Spiegel wird eigentlich immer rechts und senkrecht zur optischen Achse gezeichnet.

Strahlen, die parallel zur optischen Achse verlaufen, d.h. die senkrecht auf den Spiegel als Ganzes auftreffen, heissen Parallelstrahlen.

Brennpunkt und Brennpunktstrahlen

Parallele Strahlen, die auf einen Konkavspiegel treffen, werden von ihm zum Brennpunkt gespiegelt, d.h. alle Parallelstrahlen werden zu sog. Brennpunktstrahlen.

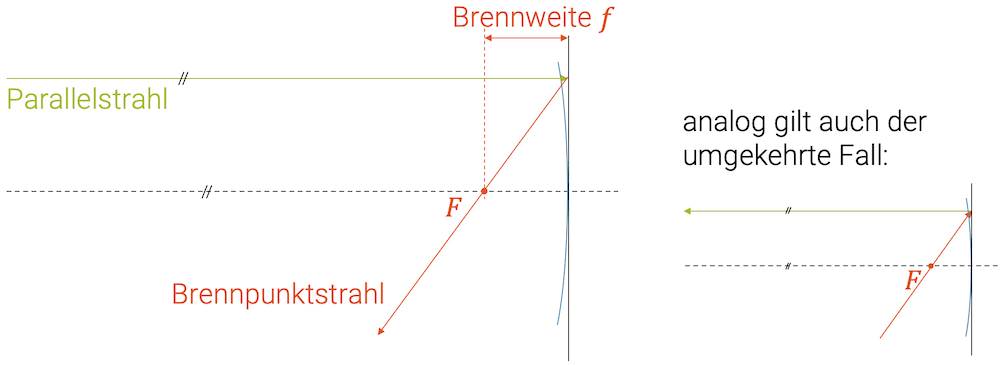
Parallelstrahlen werden durch den Konkavspiegel als Brennpunktstrahlen reflektiert

Brennpunktstrahlen werden durch den Konkavspiegel als Parallelstrahlen reflektiert

Sonnenstrahlen sind quasi-parallel, d.h. sie können von einem Konkavspiegel in einen einzigen Punkt zurückreflektiert werden. Weil die ganze Energie der parallelen Strahlen sich in diesem Punkt aufkonzentriert, entsteht dort eine sehr hohe Energiedichte, die ein Material leicht zum Brennen bringen kann. Von da her kommt der Name Brennpunkt.

Als Vorsichtsmassnahme ist es wichtig, dass nicht gebrauchte Konkavspiegel nicht einfach so herumstehen dürfen, da sie mit entsprechender Sonneneinstrahlung einen Brand verursachen können.

Der Brennpunkt wird im Normalfall mit \(F\) abgekürzt, stellvertretend für Fokus (lateinisch focus = Feuerstätte). Der Abstand des Brennpunkts zur Spiegelebene ist die sog. Brennweite \(f\).

Da Konkavspiegel nur sehr schwach gekrümmt sind, gilt die Konvention, dass die Konstruktion der Strahlen an einem vertikalen Strich vorgenommen wird. Die Krümmung des Spiegels kann zwar angedeutet werden, die Reflexion wird aber am vertikalen Strich gezeichnet und nicht am angedeuteten Spiegel.

Beachte: Weil in der Optik die Zeitumkehr gilt, gibt es auch den umgekehrten Fall, dass Brennpunktstrahlen in den Konkavspiegel einfallen und zu Parallelstrahlen werden. Das wird bei Scheinwerfern oder bei der Taschenlampe benutzt. Die Lichtquelle wird in den Brennpunkt gesetzt und die von der Lichtquelle ausgehenden Strahlen (alles Brennpunktstrahlen) werden am Konkavspiegel zu Parallelstrahlen reflektiert.

Lichtquellen mit radialen Strahlen, die von einer Punktlichtquelle ausgesendet werden, haben eine Lichtintensität, die mit dem Quadrat des Abstands abnimmt. Lichtquellen mit parallelen Strahlen behalten ihre Intensität, d.h. mit Hilfe der Konkavspiegel können Strahlen erzeugt werden, die weite Distanzen zurücklegen können, ohne dabei stark abzuschwächen.

Scheitelpunktstrahlen

Jeder gewölbte Spiegel hat einen Scheitelpunkt. Das ist der Punkt durch welchen die optische Achse verläuft.

In der unmittelbaren kleinen Umgebung um den Scheitelpunkt herum steht die Spiegelfläche genau senkrecht auf der optischen Achse. Strahlen, die dort auftreffen, werden gleich gespiegelt, wie wenn sie auf einen planaren (ebenen) Spiegel aufgetroffen wären.

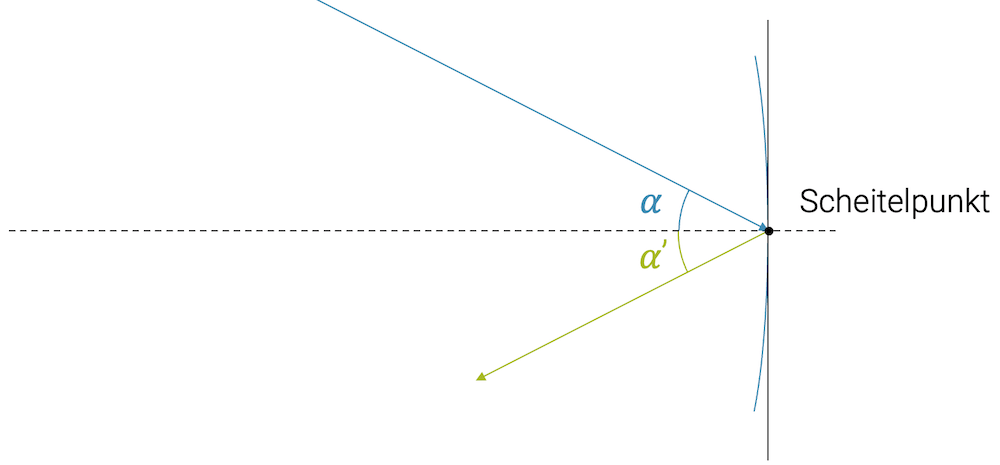
Der Strahl trifft auf den Scheitelpunkt mit einem Einfallswinkel \(\alpha\). Gemäss Reflexionsgesetz wird der Strahl mit einem Reflexionswinkel \(\alpha ‘\) reflektiert.

Scheitelpunktstrahlen werden durch den Konkavspiegel als Scheitelpunktstrahlen mit gleichem Winkel reflektiert (Reflexionsgesetz)

Beispiel

Konstruiere die Reflexionen der drei gezeichneten Strahlen am Konkavspiegel.

Lösung

Der oberste Strahl ist ein Scheitelpunktstrahl, d.h. er wird so reflektiert, dass der Reflexionswinkel gleich dem Einfallswinkel ist. Der mittlere Strahl ist ein Brennpunktstrahl, weil er durch den Brennpunkt \(F\) verläuft. Am Konkavspiegel reflektiert er als Parallelstrahl, parallel zur optischen Achse. Der unterste Strahl ist parallel zur optischen Achse, d.h. es handelt sich um einen Parallelstrahl, der nach dem Konkavspiegel zu einem Brennpunktstrahl wird.

Mittelpunktstrahlen bei sphärischen Spiegeln

Viele Konkavspiegel sind sphärisch, d.h. sie entsprechen einem Ausschnitt aus der Oberfläche einer sehr grossen Kugel. Solche Spiegel sind zwar aufwendiger als planare Spiegel, aber sie sind einfacher herzustellen, als parabolische Spiegel.

Die ideale Form mit einem präzisen Brennpunkt ist die, um optische Achse rotierte Parabel.

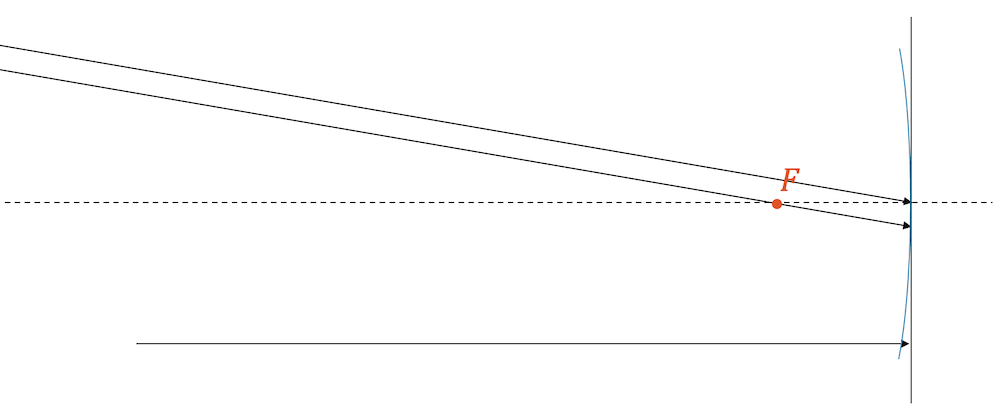
Beim sphärischen Spiegel ist der Brennpunkt leicht “verschmiert”. Die Kugel, zu welcher die Spiegeloberfläche gehört, hat einen Mittelpunkt auf der optischen Achse. Falls ein Strahl durch diesen Mittelpunkt verläuft, trifft er notwendigerweise radial, d.h. senkrecht auf die Spiegeloberfläche (Einfallswinkel 0° zum Lot).

Damit ist klar, dass ein solcher Strahl auch senkrecht reflektiert werden muss (Reflexionswinkel 0° zum Lot).

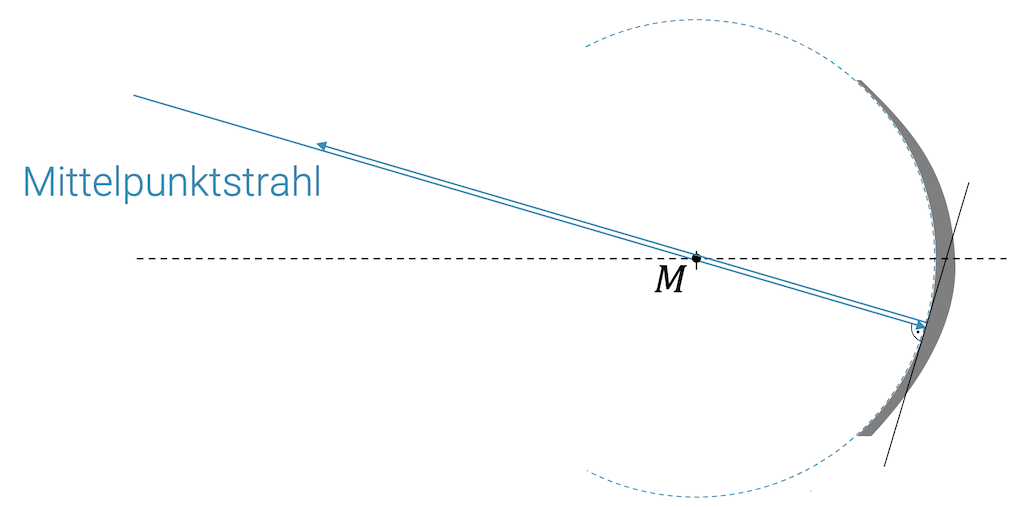
Deshalb können wir bei sphärischen Spiegeln die Mittelpunktstrahlen als Mittelpunktstrahlen zurück reflektieren lassen. Sie gehen genau dorthin zurück, woher sie gekommen sind.

Entstehung eines reellen Bilds

Bei grossem Abstand (im Vergleich zur Brennweite) entsteht ein verkleinertes, umgekehrtes, reelles Bild.

Für die Konstruktion benutzen wir zwei Strahlen, die von der Flammenspitze ausgehen: den Parallel- und den Brennpunktstrahl. Gemäss den Regeln der speziellen Strahlen bei gewölbten Spiegeln, wird der Parallelstrahl zu einem Brennpunktstrahl und der Brennpunktstrahl wird zu einem Parallelstrahl.

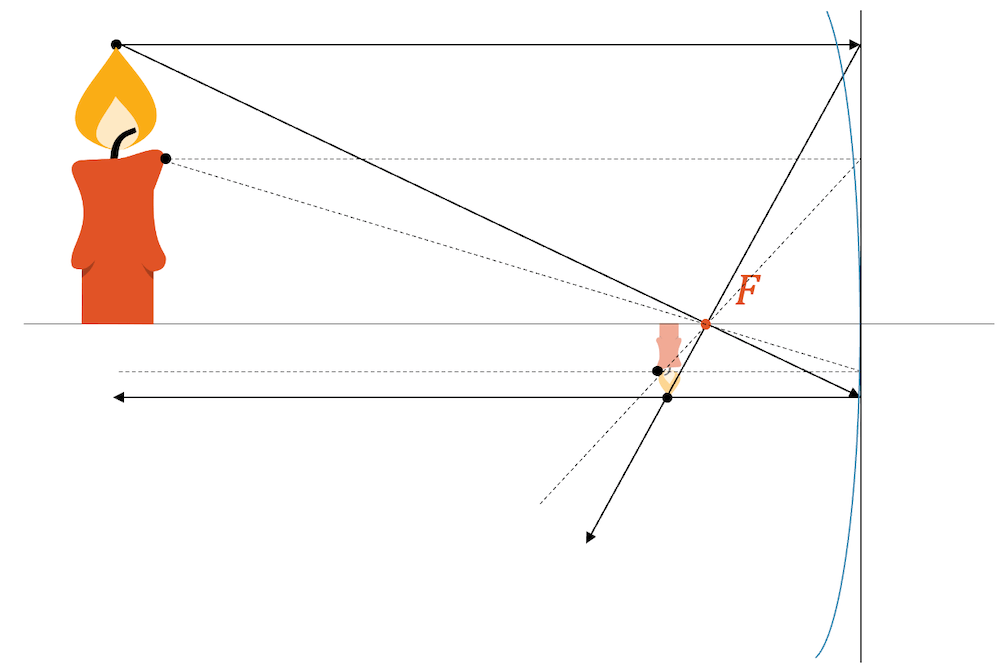
Die beiden reflektierten Strahlen kreuzen sich in einem Punkt. Das ist der Bildpunkt der Flammenspitze.

Obwohl wir nur den Parallel- und den Brennpunktstrahl von der Flammenspitze gezeichnet haben, reflektieren alle anderen Strahlen, die von der Flammenspitze ausgesendet worden sind, auch genau durch diesen Bildpunkt.

Da der Bildpunkt aus reellen, physikalisch vorhandenen Strahlen besteht, ist es ein reeller Bildpunkt der Flammenspitze, der zu einem reellen Bild der Kerze gehört.

Wir haben deshalb einen Punkt, vor dem Spiegel, der Strahlen in fast alle Richtungen aussendet – genau wie die Original-Flammenspitze. Wir sehen deshalb diesen Bildpunkt, wie ein reelles Objekt, obwohl es sich um ein Bild handelt! 😮

Für alle anderen Punkte, die zur Kerze gehören, können wir genau gleich die Parallel- und Brennpunktstrahlen sich kreuzen lassen und erhalten deren Bildpunkte vor dem Spiegel. Da die Kerze auf der optischen Achse steht, wären Strahlen von ihrer Unterkante Scheitelpunktstrahlen, die senkrecht auf den Spiegel auftreffen und somit auch wieder senkrecht reflektiert werden.

Aus alle den Bildpunkten erhalten wir das umgekehrte reelle Bild des Gegenstands (hier eine Kerze).

Wird der Gegenstand relativ nahe an den Brennpunkt heran geschoben, erhalten wir mit der gleichen Konstruktion der beiden Strahlen einen Bildpunkt, der weiter vom Spiegel entfernt ist. Das Bild der Kerze ist auch dieses Mal umgekehrt und reell. Allerdings ist das Bild dieses Mal grösser als der Gegenstand.

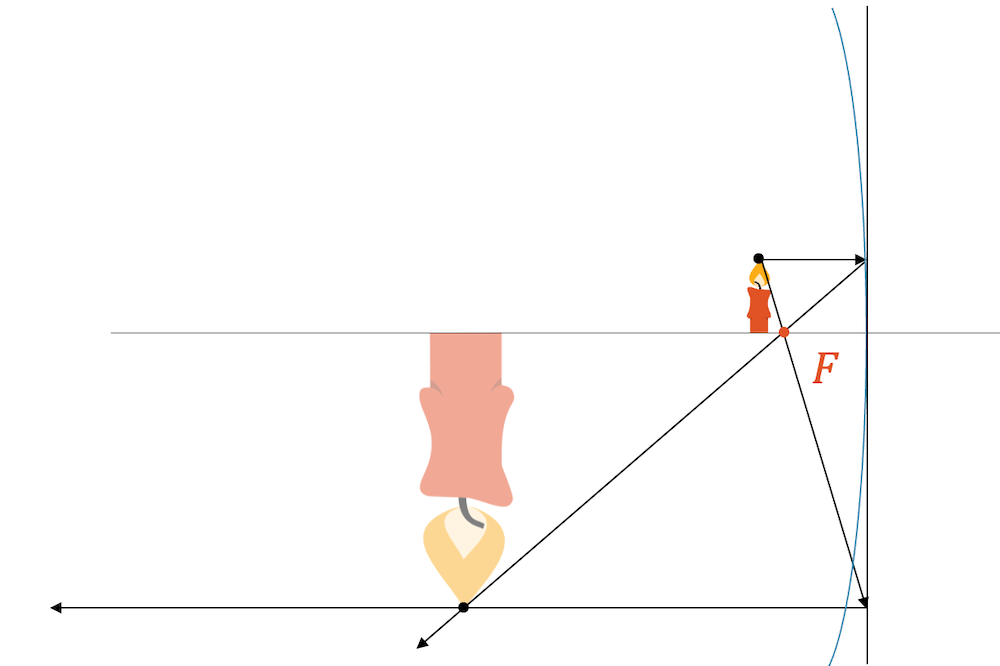
Entstehung eines virtuellen Bilds

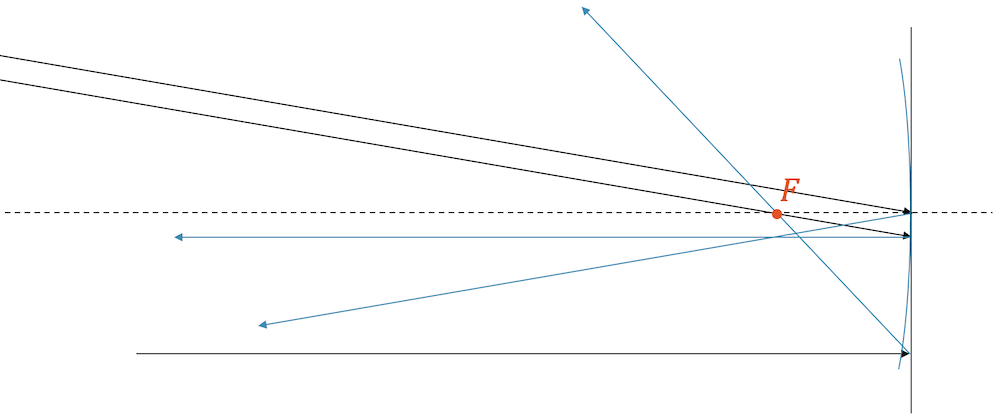
Schieben wir die Kerze noch näher an den Spiegel heran, so entsteht ein aufrechtes Bild, das dieses Mal aber hinter dem Spiegel ist, d.h. es muss virtuell sein, weil die Lichtstrahlen gar nicht hinter den Spiegel gelangen können.

Für die Konstruktion nehmen wir wieder den Parallel- und den Brennpunktstrahl der Flammenspitze.

Der Brennpunktstrahl geht gar nicht durch den Brennpunkt, sondern verläuft so, als käme er vom Brennpunkt. Tatsächlich wurde er ja von der Flammenspitze abgegeben. Aus Sicht des Konkavspiegels ist es aber ein Brennpunktstrahl, der dann zum Parallelstrahl reflektiert wird.

Der Parallelstrahl kann ganz normal konstruiert werden, indem er nach dem Spiegel durch den Brennpunkt verläuft.

Die beiden neu konstruierten Strahlen verlaufen vom Spiegel weg, jedoch verlaufen sie auseinander, d.h. sie werden sich sicherlich nicht in einem Bildpunkt kreuzen! Die Bildung eines reellen Bildpunkts ist ausgeschlossen.

Die beiden Strahlen kreuzen sich in ihrer virtuellen Verlängerung hinter dem Spiegel. 👀

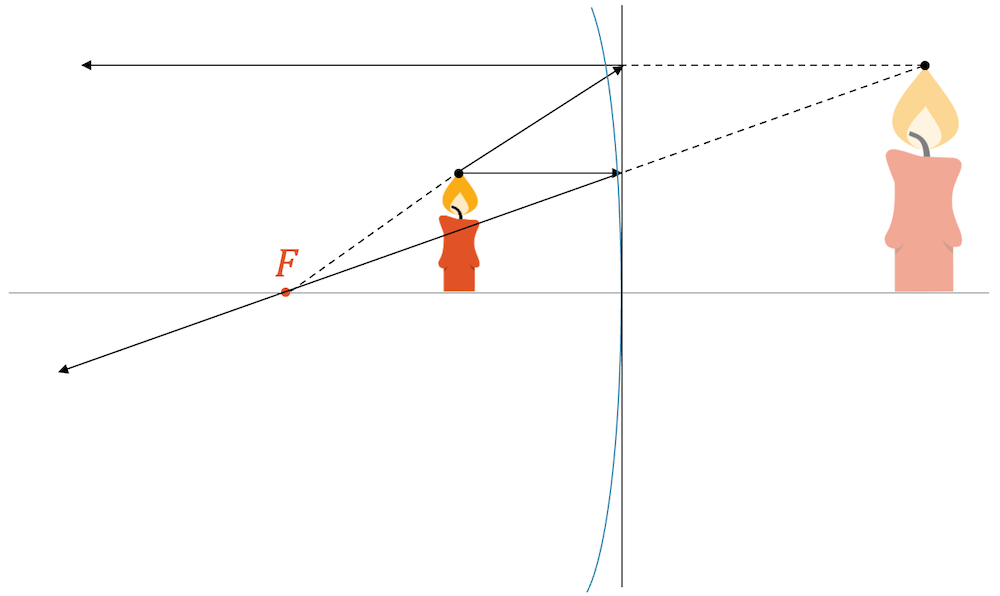
Für einen Betrachter der beiden Lichtstrahlen kommen beide ja aus dem gleichen Punkt heraus, denn der Betrachter nimmt immer an, dass Strahlen geradlinig verlaufen. Der Punkt ist ein scheinbarer Bildpunkt oder eben, ein virtueller Bildpunkt unserer Flammenspitze. Wir setzen die Kerze ein und fertig ist das virtuelle, aufrechte und vergrösserte Bild der Kerze.

Diese Konstruktion entspricht der Anwendung des Schmink- oder Rasierspiegels, wo wir uns im Spiegel betrachten können und ein vergrössertes Bild von uns sehen.

Verschiedene Bilder bei Konkavspiegeln: Übersicht

Fassen wir nochmals alle Bilder zusammen, die der Konkavspiegel (Hohlspiegel) erzeugen kann:

• Verkleinertes, umgekehrtes, reelles Bild (bei grosser Gegenstandsweite, \(g>2f\))
• Vergrössertes, umgekehrtes, reelles Bild (bei mittlerer Gegenstandsweite, \(g < 2f\))
• Verkleinertes, aufrechtes, virtuelles Bild (bei kleiner Gegenstandsweite, \(g<f\))

Die verschiedenen Bildarten sind am Anfang etwas verwirrend. Die folgende Grafik soll hier etwas mehr Übersicht geben:

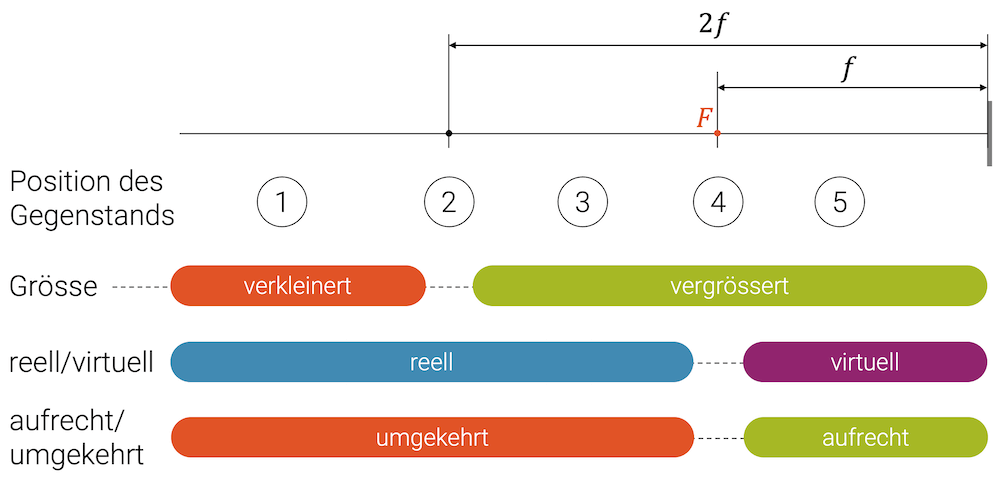
• Position 1: Ganz links in der Grafik haben wir die Positionen 1 in welcher der Gegenstand noch weit vom Spiegel ist. Es entsteht ein verkleinertes, reelles und umgekehrtes Bild, genauso wie wir es in unserer ersten Strahlenkonstruktion gesehen haben.
• Position 2: In dieser Position ist das Bild immer noch reell und umgekehrt. Allerdings befindet sich das Bild am gleichen Ort wie der Gegenstand, d.h. \(b = g\). Mit Hilfe des Strahlensatzes der Optik erhalten wir: \(B=G\), d.h. das Bild ist genau gleich gross wie der Gegenstand.
• Position 3: Diese Situation entspricht unserem zweiten Beispiel, das wir weiter oben besprochen haben. Das Bild ist immer noch reell und umgekehrt, jedoch ist es jetzt weiter vom Spiegel entfernt und deshalb im Vergleich zum Gegenstand vergrössert.
• Position 4: In der Position 4 entsteht etwas ganz Spezielles: Wenn wir versuchen die Konstruktion wie im dritten Beispiel auszuführen, erhalten wir zwei Strahlen, die zueinander parallel verlaufen, d.h. sie bilden weder einen reellen Bildpunkt vor dem Spiegel, noch bilden sie einen virtuellen Bildpunkt hinter dem Spiegel: Sie bilden gar keinen Bildpunkt! In dieser Position entsteht kein Bild.
• Position 5: Genug nahe am Spiegel entsteht, wie im dritten Beispiel gezeigt, ein vergrössertes, virtuelles und aufrechtes Bild.

Simulation

Unter dem folgenden Link findest du eine sehr gelungene Simulation, die dir die Strahlenverläufe konstruiert. Nimm die Spitze des Gegenstands und verschiebe ihn näher zum Spiegel oder weiter weg. Für den Konvexspiegel, bewegst du den Gegenstand einfach auf die andere Seite des Spiegels.