Potenzielle Energie (Lageenergie)

Verschiedene Arten der potenziellen Energie

Was hat ein Apfel, der am Baum auf einer Höhe von 2 Metern über Boden hängt, was ein Apfel am Boden nicht hat?

Er hat eine höhere Lage und er kann durch seinen Fall etwas bewirken, d.h. er hat auf 2 Metern Höhe die Fähigkeit Arbeit zu verrichten, d.h. er hat Energie gespeichert.

Solange der Ast den Apfel festhält, behält der Apfel seine Fähigkeit Arbeit zu verrichten. Diese gespeicherte Fähigkeit ist die potenzielle Energie (oder auch Lageenergie).

Sobald die Gegenkraft verschwindet, wirkt nur noch die Gravitationskraft bzw. die Gewichtskraft und der Apfel fällt gemäss Newtons Zweitem Gesetz vom Baum.

Der Apfel verliert an Höhe und verliert damit auch seine potenzielle Energie. Er wird beschleunigt und wandelt die potenzielle Energie in kinetische Energie (Bewegungsenergie) um. Ist der Apfel einmal am Boden angekommen, hat er keine potenzielle Energie mehr. 🍎

Die potenzielle Energie bzw. potentielle Energie (mit “t”) wird oft als Lageenergie vereinfacht. Sie ist, zusammen mit der kinetischen Energie, eine sehr fundamentale Energieform der Physik. Es gibt auch potenzielle Energie aufgrund von anderen Kräften als der Gewichtskraft. Wir werden hier die folgenden drei Kräfte diskutieren:

• Gewichtskraft \(\rightarrow\) Hubarbeit \(\rightarrow\) potenzielle Energie (Lageenergie)
• Federkraft \(\rightarrow\) Spannarbeit \(\rightarrow\) potenzielle Energie aufgrund der Federkraft
• Coulombkraft \(\rightarrow\) Arbeit \(\rightarrow\) potenzielle Energie aufgrund der Coulombkraft

Es gibt noch weitere Beispiele. Voraussetzung ist ein sog. konservatives Kraftfeld, was die drei obigen Kräfte erfüllen. Einfach gesagt: Wenn folgendes erfüllt ist, ist die Kraft konservativ und es gibt eine potenzielle Energie dafür:

• vom Zustand 0 zum Zustand 1: Wir müssen gegen eine Kraft Arbeit verrichten, was eine bestimmte Menge an Energie braucht
• vom Zustand 1 zurück zum Zustand 0: Die Kraft verrichtet jetzt Arbeit und gibt uns die gleiche Energie wieder zurück

Wenn wir vom Zustand 0 \(\rightarrow\) Zustand 1 \(\rightarrow\) Zustand 0 gehen, sind wir bei der potenziellen Energie wieder auf dem gleichen Energieniveau.

Um dies zu verdeutlichen: Die Reibungskraft ist keine konservative Kraft: Wir kriegen die Energie nicht wieder zurück. Im Gegenteil: Egal in welche Richtung, nimmt uns die Reibungskraft Energie weg und wandelt sie in thermische Energie um. Es gibt deshalb keine potenzielle Energie für die Reibungskraft. 🧐

Potentielle Energie Definition

Potentielle Energie Symbol: \(E_{\text{pot}}\) (manchmal auch \(U\))

Potentielle Energie Einheit: \(\text{J}\) (Joule, übliche Einheit der Energie)

Beachte, dass der absolute Betrag der potenziellen Energie keine physikalische Bedeutung hat. Ich werde es an einem Beispiel erklären:

Die potenzielle Energie eines Apfels auf dem Boden wird von uns auf null gesetzt. Das ist eine willkürliche Entscheidung von uns. Auf einer Höhe von 2 m über dem Boden hat der Apfel entsprechend mehr potenzielle Energie, nämlich den Betrag der Hubarbeit, die es braucht, um ihn dorthin zu bringen.

Bei mir zu Hause wäre der Boden auf etwa 550 Metern über Meeresspiegel. Eigentlich ist der Apfel auf grosser Höhe, obwohl am Boden! Dann müsste ich mich aber fragen: Warum Meeresspiegel und nicht Meeresgrund? Das wäre noch mehr Höhe und somit noch mehr potenzielle Energie! Die einzige Referenz, die wirklich Sinn machen würde, wäre der Schwerpunkt der Erde.

Wir vereinfachen die Sache aber so, dass wir uns nicht für den absoluten Wert der potenziellen Energie interessieren, sondern wir vergleichen potenzielle Energien (relativ) und benutzen dazu eine gemeinsame, wenn auch willkürliche Definition, wie z.B. “Für diesen Boden sei die potenzielle Energie null”.

Weil das Niveau für \(E_{\text{pot}}=0\) willkürlich definiert werden darf, können potenzielle Energien auch negative Werte annehmen.

Potenzielle Energie Gewichtskraft

Hier ein paar weitere Beispiele der potenziellen Energie aufgrund der Lage:

• Ein Regentropfen oder eine Schneeflocke haben beim Verlassen der Wolke potentielle Energie, die sie zum freien Fall beschleunigt
• Wasser(tropfen) in einem Fluss kann seine Energie in einer Wasserturbine für die Stromproduktion abgeben.
• Ein Pumpspeicherkraftwerk nutzt überschüssige elektrische Arbeit für das Pumpen von Wasser in den hochgelegenen Stausee und speichert damit potenzielle Energie.
• Felsen und Steine haben oben auf dem Berg potentielle Energie, die sie beschleunigen könnte (Bergsturz)
• Potentielle Energie schiefe Ebene: Ein Skater kann sich, ohne Anstossen, die schiefe Ebene herunterrollen lassen

Potenzielle Energie Formel (Formel für Lageenergie). Die Herleitung steht weiter unten.

\[ E_{\text{pot}} = mgh \]

Beachte, dass diese Formel nur in der von Menschen üblicherweise eingenommene Nähe zur Erdoberfläche gilt, d.h. von der Erdoberfläche bis zu einer üblichen Flughöhe. In dieser “Schicht” gilt die Erdbeschleunigung \(g=9.81\,\frac{\text{m}}{\text{s}^2}\).

Ausserhalb dieser Schicht, d.h. für sehr grosse Flughöhen oder für sehr tiefe Orte in der Erde, gilt die Gewichtskraft \(F_g=mg\) nicht mehr. Du musst dann die Gravitationskraft \(F_G=G\cdot\frac{Mm}{r^2}\) verwenden, die den Einfluss des Abstands zum Erdinnern berücksichtigt.

Hier ein anderes Beispiel für die potenzielle Energie oder Lageenergie: Unmengen von Wasser sind auf einer grossen Höhe in einem Stausee gespeichert.

Die Gewichtskraft zieht am Wasser nach unten, doch das Wasser wird vom Stausee zurückgehalten.

In der Nacht und wenn allgemein zu viel elektrischer Strom im Stromnetz vorhanden ist, wird zusätzliches Wasser vom Tal wieder nach oben gepumpt. Die Hubarbeit, die da geleistet wird, braucht sehr viel Strom. Doch die Energie wird in Form von potenzieller Energie im Wasser gespeichert.

Beim Herablassen des Wassers kann diese potenzielle Energie zu einem späteren Zeitpunkt wieder zurückgewonnen werden, z.B. dann, wenn ein erhöhter Strombedarf herrscht.

Die Wasserkraftwerke, die auf diese Weise mal Strom brauchen, Energie speichern und dann wieder Strom produzieren, heissen Pumpspeicherkraftwerke.

Egal, ob wir Wasser nach oben pumpen oder einen Apfel anheben, wir leisten Hubarbeit. Das Anheben des Apfels geht nur, wenn wir Hubarbeit leisten und dabei diese unsichtbare Feder etwas dehnen. 👀

Die Hubarbeit \(W\), die wir verrichten, ist dann als potenzielle Energie im Apfel gespeichert.

Potentielle Energie Federkraft

Beispiele potentielle Energie aufgrund einer Federkraft:

• Potentielle Energie einer Feder (gespannt oder gestaucht): Die gespannte Feder könnte etwas antreiben
• Potentielle Energie eines Gases, das unter Überdruck steht: Das Gas kann bei seiner Expansion andere Objekte beschleunigen (z.B. Explosion)

In der Physik reden wir oft von Federn und meinen damit metallische Federn. Die sind ja nicht besonders interessant. Warum reden wir immer von ihnen?

Sie stehen stellvertretend für jede Art von elastischem Material.

Selbst eine Brücke aus armiertem Beton ist elastisch und verhält sich wie eine sehr starke Feder!

Egal, ob Brücke, Gummiband oder Metallfeder: Im ungespannten Zustand ist die potentielle Energie der Feder null. Dehnen (oder stauchen) wir die Feder, so nimmt die potentielle Energie zu.

Beachte aber, dass die Federkraft dem Hook’schen Gesetz folgt, und die Gravitationskraft dem Gravitationsgesetz. Die beiden Kräfte verhalten sich anders:

• Die Gravitationskraft nimmt mit zunehmendem Abstand ab
• Die Federkraft nimmt mit zunehmender Dehnung zu

Wir können deshalb die potenzielle Energie für diese Kräfte nicht mit der gleichen Formel berechnen.

Die Spannarbeit, die wir an einer Feder mit Federkonstante \(k\) verrichten, wenn wir sie von der Dehnung \(s_1\) zur Dehnung \(s_2\) bringen, ist:

\[ W = E_{\text{pot},1} \; – \; E_{\text{pot},0} \]

\[ W = \frac{1}{2} \cdot k \cdot s_1^2 \; – \; \frac{1}{2} \cdot k \cdot s_0^2 \]

Daraus folgt für die potenzielle Energie aufgrund der Federkraft:

\[ E_{\text{pot}} = \frac{1}{2} k \Delta x^2 \]

Potentielle Energie Coulombkraft

Wenn wir eine elektrische Ladung, z.B. ein Elektron, gegen eine anziehende Coulombkraft wegziehen, braucht dieser Vorgang Arbeit. Auch hier ist es, wie wenn wir eine unsichtbare Feder dehnen würden.

Das weg gezogene Elektron speichert die Arbeit, die an ihm verrichtet worden ist als potenzielle Energie, die es jederzeit wieder abgeben kann, wenn es wieder zurück gelassen wird.

Die potenzielle Energie, die ein solches Elektron innehat, besagt etwas darüber, wie viel Fähigkeit es gespeichert hat, Arbeit zu verrichten. Wir erinnern uns an den Apfel: Ein Apfel auf grosser Höhe hat mehr Energie gespeichert, als ein Apfel auf kleiner Höhe. Ähnlich gibt es Elektronen, an welchen viel Arbeit verrichtet worden ist und solche, die nur wenig Energie erhalten haben.

Wenn wir diese Menge an Energie durch die Ladung dividieren, erhalten wir die Grösse elektrische Spannung \(U\). Sie ist definiert als die potenzielle Energie \(E_{\text{pot}}\) pro Ladung \(Q\):

\[ U = \frac{E_{\text{pot}}}{Q} \]

Daraus folgt für die potenzielle Energie:

\[ E_{\text{pot}}= U \cdot Q \]

Wird das Elektron komplett vom Atom getrennt, so wird aus dem Atom ein sog. Ion. Die Arbeit, die dafür aufgewendet werden musste, ist die sog. Ionisationsenergie.

Das Elektron spürt das Atom nicht mehr, wenn wir es genug weit weg ziehen. Eigentlich hat es jetzt die maximal mögliche potenzielle Energie. Wir setzen sie auf null, d.h. \(E_{\text{pot}}=0\) bedeutet, dass das Elektron frei ist. Das ist eine reine Definitionssache.

Das Elektron, das noch zum Atom gehört und nahe am Atomkern ist, hat deshalb negative potenzielle Energie, nämlich genau so viel im Negativen, wie es braucht, um es aus seinem “Topf” zu befreien.

Herleitung der potenziellen Energie (Lageenergie)

Ein Apfel mit der Masse \(m\) ist im Zustand 0 am Boden, der selber auf der Höhe \(h_0\) ist. Heben wir den Apfel auf die Höhe \(h_1\) an, so verrichten wir Hubarbeit an ihm.

Wir wissen, dass das Verrichten von Arbeit eine Übertragung von Energie ist, d.h. der Apfel kriegt potenzielle Energie: Am Anfang hat er die Energiemenge \(E_{\text{pot},0}\) und danach die Energiemenge \(E_{\text{pot},1}\). Die Energiemenge, die der Apfel gekriegt hat, ist somit die Differenz zwischen nachher und vorher:

\[ W_{0 \rightarrow 1} = \Delta E = E_{\text{pot},1} – E_{\text{pot},0} \]

Wir erinnern uns auch, dass die physikalische Arbeit die Wirkung von Kraft über eine Wegstrecke ist, nämlich “Kraft mal Weg”:

\[ W=F \cdot \Delta s \]

In unserem Fall ist die Wegstrecke \(\Delta s = h_1 – h_0\) die Differenz der beiden Höhen. Die Kraft \(F\), die wirken muss, ist gleich der Gewichtskraft des Apfels: \(F=F_g = mg\)

\[ W_{0 \rightarrow 1} = F_g \cdot \Delta s = mg \cdot (h_1 – h_0) \]

Ausmultipliziert, erhalten wir

\[ W_{0 \rightarrow 1} = mgh_1 – mgh_0 \]

Nehmen wir nochmals die Gleichung von oben und vergleichen sie mit der eben erhaltenen Gleichung:

\[ W_{0 \rightarrow 1} = E_{\text{pot},1} – E_{\text{pot},0} \]

\[ W_{0 \rightarrow 1}= mgh_1 – mgh_0 \]

Wir erkennen, dass offenbar \(E_{\text{pot},1} = m g h_1\) und \(E_{\text{pot},0} = m g h_0\) gilt. Allgemein gilt deshalb:

\[ E_{pot} = m g h \]

Beachte, dass die Höhe \(h\) relativ zu einem willkürlich gewählten Referenzsystem gemessen wird. Meistens wählen wir die Höhe null \(h=0\) für den Erdboden.

Damit sind auch “negative” Höhen \(h\) möglich, nämlich wenn wir unterhalb des Null-Niveaus sind, z.B. im Kellergeschoss. Wenn wir eine Masse auf eine Höhe unterhalb des Erdbodens absenken (z.B. ein Steinchen in einen Brunnen werfen), nimmt dieser Körper eine negative potenzielle Energie an.

Potentielle Energie in kinetische Energie umwandeln

Mit Gegenkraft ist der Apfel am Baum im Kräftegleichgewicht und behält, gemäss Newtons Erstem Gesetz seine Geschwindigkeit, die null ist. Er bleibt in Ruhe und beschleunigt nicht nach unten.

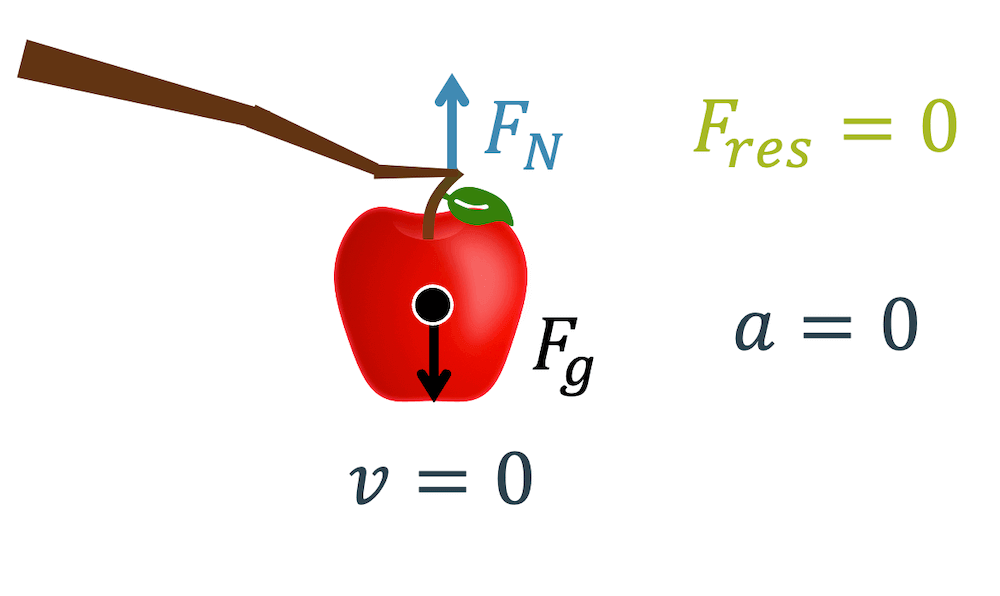
Fällt die Gegenkraft \(F_N\) weg, fällt das Kräftegleichgewicht weg und der Apfel wird beschleunigt. Die potenzielle Energie nimmt ab, indem die Höhe abnimmt. Aufgrund der Energieerhaltung verliert der Apfel keine Energie, sondern sie wird nur in eine andere Form, in kinetische Energie (Bewegungsenergie) umgewandelt.

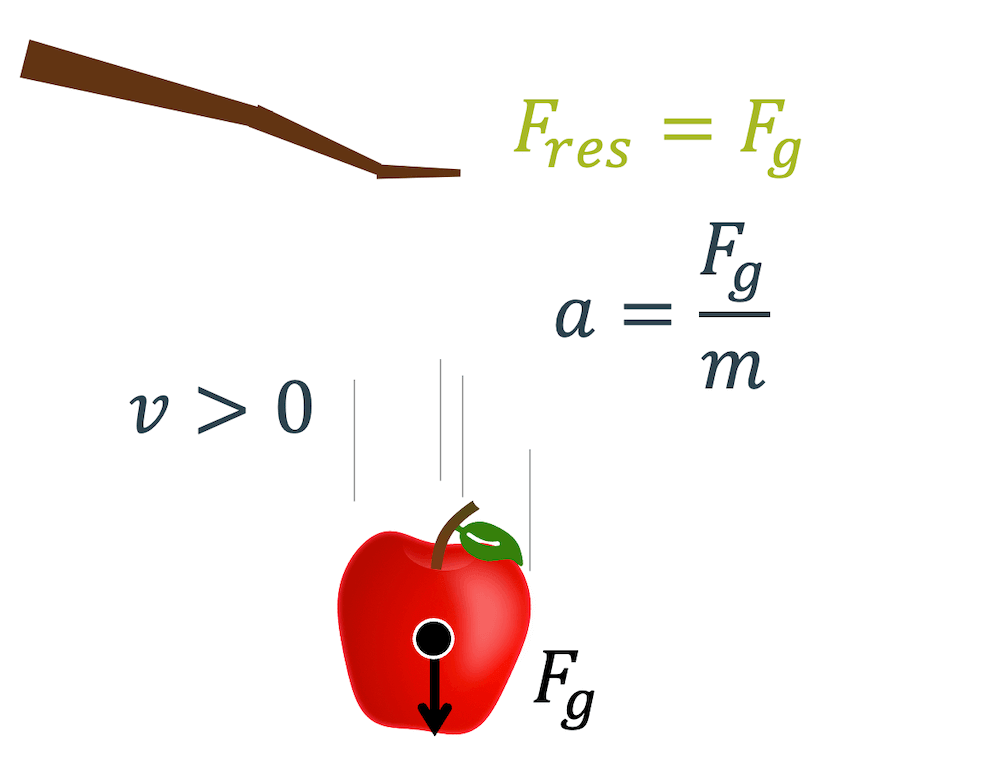
Beispiele potentielle Energie in kinetische Energie umwandeln:

• Regentropfen, Schneeflocken, Hagelkorn etc. fallen im freien Fall herunter
• Felsen, Geröll, Steine etc. fallen die schiefe Ebene (Hang) herunter
• Fahrradfahrer, Skater etc. lassen sich die schiefe Ebene (Hang bzw. Strasse) herunterrollen
• Eine gespannte Feder spickt eine Kugel weg
• Die Explosion des Schiesspulvers schiesst die Kugel weg
• Nach der Kernspaltung stossen sich die beiden positiven Atomkerne von einander weg (Atomkraft)