Inhalt
Das Wichtigste in Kürze
Die Leistung \(P\) ist eine Menge an Energie \(\Delta E\), die in einer bestimmten Zeitspanne \(\Delta t\) umgesetzt worden ist. Beispielsweise ist die Leistungsaufnahme eines Geräts die Energie pro Zeit, die das Gerät “verbraucht”. Oft wird die Leistung auch als die Arbeit \(W\) berechnet, die innerhalb der Zeitspanne \(\Delta t\) verrichtet worden ist:
\[ P = \frac{\Delta E}{\Delta t} = \frac{W}{\Delta t} \]
Videos
Häufigste Fragen

Image by Agê Barros, shared on Unsplash
Definitionen
Abkürzung: \(P\) (engl. “power”, franz. “puissance”)
Einheit: \([P] = \mathrm{\frac{J}{s}} = \mathrm{W}\) (Watt)
Die Einheit Pferdestärken (\(\mathrm{PS}\)) ist noch sehr gebräuchlich, v.a. für die Leistung von Motoren. Sie wird in der Physik aber nicht mehr verwendet.
Hohe Leistung: gleich viel Arbeit in kürzerer Zeit
Eine Masse wird angehoben. Dazu muss Hubarbeit geleistet werden. Wir nehmen an, dass es 60 J Arbeit sind.
Wenn wir für das Verrichten dieser Hubarbeit 20 Sekunden benötigen, dann errechnet sich die Leistung \(P\):
\[ P = \frac{W}{\Delta t} = \frac{60\,\mathrm{J}}{20\,\mathrm{s}} = 3\,\mathrm{W} \]
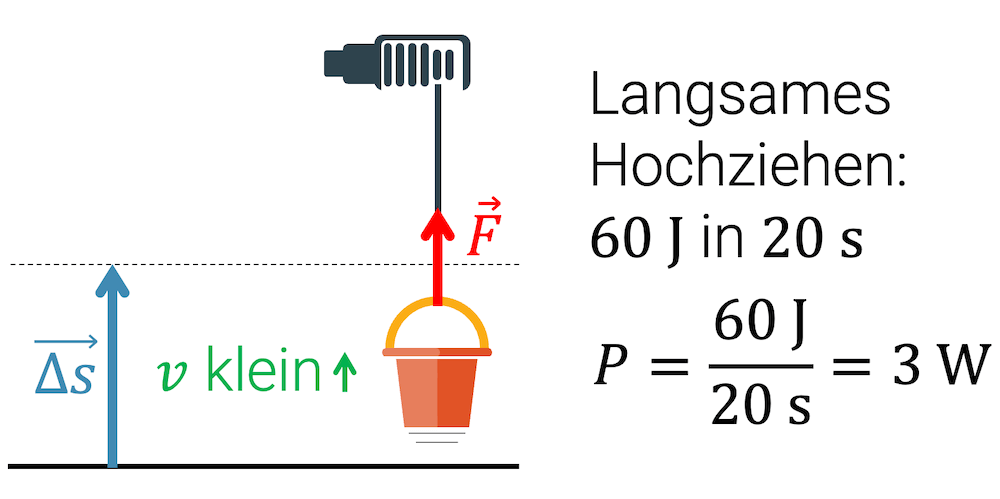
Für eine Leistung von 3 W reicht ein kleiner Motor.
Wenn wir aber die gleiche Arbeit in kürzerer Zeit verrichten möchten, dann ändert sich auf der Energie-/Arbeitsseite nichts. Die Masse ist immer noch gleich schwer, die Höhe ist immer noch gleich.
Was sich ändert ist die Zeit \(\Delta t\).
Wenn wir die gleiche Arbeit in nur 2 Sekunden erledigt haben möchten, erhalten wir:
\[ P = \frac{W}{\Delta t} = \frac{60\,\mathrm{J}}{2\,\mathrm{s}} = 30\,\mathrm{W} \]
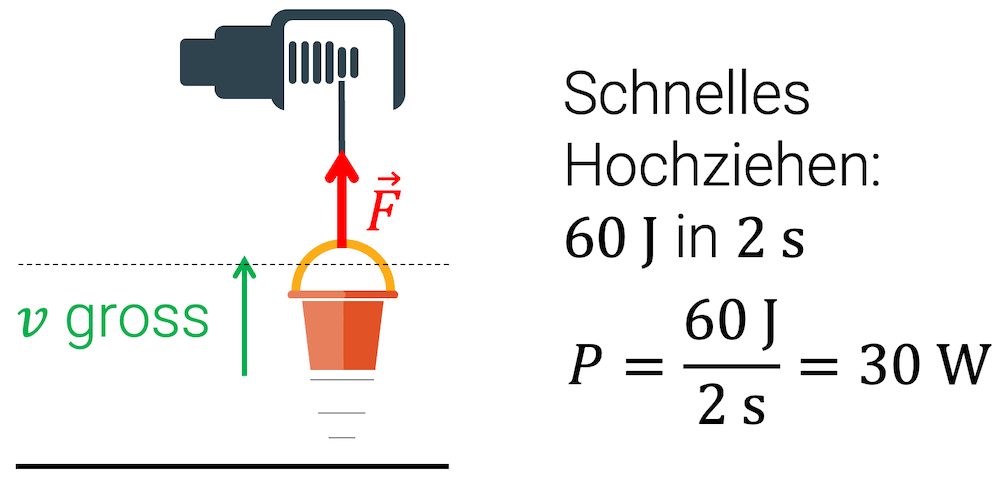
Es braucht einen grösseren Motor mit 10-facher Leistung! Dieser grössere Kranmotor kann die gleiche Last \(F\) über die gleiche Wegstrecke \(\Delta s\) anheben. Er macht es aber 10 mal schneller.
Schauen wir uns ein Beispiel an mit der Beschleunigungsarbeit:
Ein günstiger Kleinwagen kann, gleich wie ein Sportwagen, auf die erlaubte Höchstgeschwindigkeit beschleunigen. Der Sportwagen hat einen grösseren Motor, der viel mehr Leistung abgeben kann und deshalb bringt er die gleiche Beschleunigungsarbeit in viel kürzerer Zeit.
Hohe Leistung: mehr Arbeit in gleiche Zeit
Aus der Definition der Leistung als Bruch von “Arbeit über Zeit”, erkennen wir, dass wir ein grosses \(P\) haben können, wenn nicht der Nenner \(\Delta t\) klein ist, sondern einfach der Zähler \(W\) (Arbeit) gross ist:
\[ P = \frac{W}{\Delta t} \]
In unserem vorigen Beispiel kann der grosse Kranmotor in der gleichen Zeit von 20 Sekunden die Masse 10-mal höher anheben oder er kann vielleicht sogar die 10-fache Masse anheben.
“Energie bzw. Arbeit ist Leistung mal Zeit.”
Umrechnung zwischen Leistung und Arbeit/Energie
Wir nehmen die Definition der Leistung und multiplizieren die Gleichung mit der Zeitperiode \(\Delta t\):
\[ \frac{W}{\Delta t} = P \]
\[ W = P \cdot \Delta t \]
Wir erhalten einen Ausdruck für die Berechnung der Arbeit. Auf die Frage hin “Wie viel Arbeit hat der kleine Motor in 10 s geleistet?”, berechnen wir:
\[ W = 3\,\mathrm{W} \cdot 10\,\mathrm{s} = 30\,\mathrm{\frac{J}{s} \cdot s} = 30\,\mathrm{J} \]
Das ist natürlich die halbe Arbeit von vorhin, weil der Motor nur halb so lange gearbeitet hat.
Achtung Verwechslungsgefahr! Die Arbeit \(W\) hat die Einheit \(\mathrm{J}\) (Joule). Die Leistung \(P\) hat die Einheit \(\mathrm{W}\) (Watt). In der obigen Rechnung siehst du das erste \(W\) für die Arbeit und dann das zweite Mal als Einheit der Leistung in \(3\,\mathrm{W}\).
Beachte auch, dass die Einheit Kilowattstunde eine Einheit für die Energie ist. Sie entspricht analog zu \(E = P \cdot \Delta\) der Multiplikation einer Leistung mit einer Zeit:
\[ 1 \, \mathrm{kWh} = 1 \, \mathrm{kW} \cdot 1 \, \mathrm{h} \]
Eine Kilowattstunde ist die Energie, die bei einer Leistung von 1 kW über eine Stunde lang verbraucht bzw. umgesetzt worden ist.
Beispiel: Leistung eines Kühlschranks
Ein Kühlschrank im Schnitt 188 J in 10 Sekunden. Berechne seine Leistung in Watt, sowie die elektrische Arbeit, die der Kühlschrank in einem Jahr verbraucht, in Megajoule und in Kilowattstunden.

Aufgabensammlung
Lernziele
- Du kennst den Begriff der Leistung und kannst in eigenen Worten erklären, wie die Leistung mit den Grössen Arbeit bzw. Energie und Zeit zusammenhängen.
- Du kannst aufgrund einer gegebenen Energie bzw. Arbeit und unter Angabe der Zeit, die Leistung berechnen bzw. umgekehrt.
- Du kennst die Einheit Kilowattstunde (kWh) und kannst sie in MJ umrechnen bzw. umgekehrt.
Weitere Links
Leistung (Physik) (Wikipedia)
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt











Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.