Inhalt

Die Art und Weise, wie sich Wellen überlagern, ist die wohl faszinierendste Eigenschaft der Wellen. Damit werden unglaublich interessante Experimente möglich: Es entstehen alle Regenbogenfarben auf Seifenblasen, Schall kann durch zusätzlichen Schall unterdrückt werden und Licht kann sogar inmitten eines Schattens erscheinen!
Ungestörte Überlagerung

Im obigen Bild wird sehr schön ersichtlich, wie Wasser-Oberflächenwellen perfekte Kreise bilden (Ausbreitung der Welle in einem zweidimensionalen Raum). Was ausserdem auffällt ist, dass die Kreise sich gegenseitig überschneiden und durchkreuzen. Keiner der kreisförmigen Wellen wird durch eine andere Welle verformt.
Wellen überlagern sich gegenseitig ohne Störung, d.h. sie kreuzen sich und pflanzen sich dann fort, als wäre nichts passiert.
Wir können das auf bekannte Wellenarten übertragen. Der Ton von einem Instrument wird durch ein weiteres Instrument nicht gestört, sondern nur ergänzt. Auch kann man sich übers Kreuz unterhalten, d.h. die beiden Schallwellen durchkreuzen sich, ohne dass der Ton verfälscht wird. Genauso kann ein Lichtstrahl einen anderen Lichtstrahl kreuzen, ohne dass sich an den beiden Lichtstrahlen etwas ändert. Sie gehen weiter, als wären sie schon immer alleine gewesen.
Überlagerung als Summe der Wellenfunktionen
Wenn zwei Wellen sich überlagern, z.B. wenn ein Instrument einen Ton spielt und ein anderes Instrument einen höheren Ton spielt (höhere Frequenz), kommen beim Zuhörer beide Töne in gleicher Qualität an.
Nachfolgend schauen wir uns ein mathematisches Beispiel an: Die Wellenfunktion \(f_1\) wird durch die höher frequente Wellenfunktion \(f_2\) überlagert.
Jetzt werden einfach alle Ausschläge addiert. Am einfachsten schauen wir uns ein paar typische Punkte an. Bei der ersten gestrichelten Linie ist \(f_1\) auf der Höhe von etwas mehr als 1 Häuschen. Die zweite Funktion \(f_2\) ist ganz leicht unterhalb von 2 Häuschen. In Summe gibt das etwa 3 Häuschen. Wir übertragen das auf die rote Kurve unten.
Sobald \(f_1\) das erste Mal das Maximum erreicht hat, ist \(f_2\) gerade im Minimum. Die Summe ist damit 2-2 = 0 Häuschen. Die beiden Wellen löschen sich kurzzeitig aus. Die rote Kurve ist dann auf der horizontalen Achse.
Eine einfache Addition ist auch die dritte gestrichelte Linie. \(f_1\) ist bei null und \(f_2\) auch. Damit ist die Summe ebenfalls bei null.
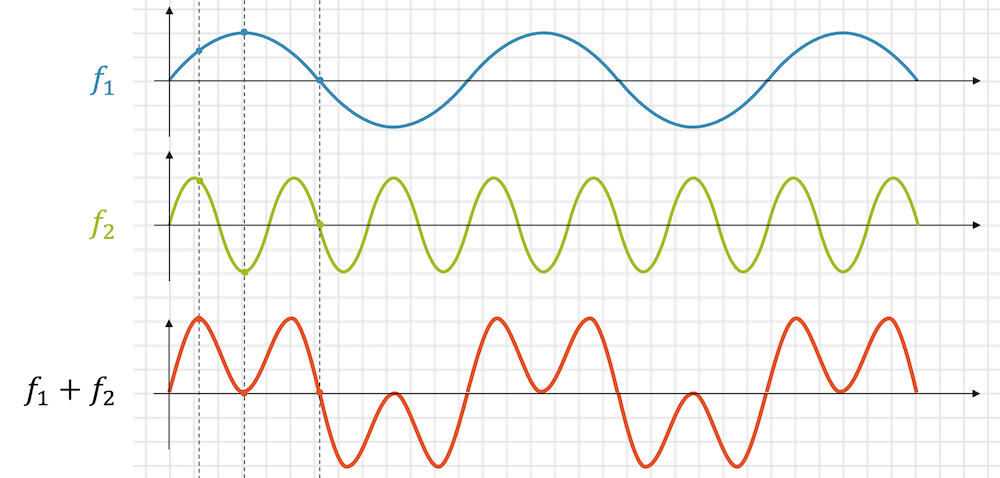
Mit solchen Überlegungen kommen wir schliesslich zum Verlauf der roten Kurve. Die Schallwelle, die den Zuhörer erreicht, wird genau diesen Verlauf haben. Sie ist nicht mehr harmonisch.
Interessant ist, dass diese Summe im inneren Ohr wieder in die beiden ursprünglichen Frequenzen aufgeteilt werden kann, so dass der Zuhörer wieder zwei Töne hört, obwohl nur eine Schallwelle zu ihm gekommen ist.
Das ist alles andere als selbstverständlich! Wenn ich 2+3 addiere und 5 erhalte, kann ich unmöglich aus der Summe 5 ablesen, dass ursprünglich 2+3 gerechnet worden ist. Diese Information ist verloren gegangen. Die Summe hätte auch 1+4 oder 0+5 oder unendlich viele andere Kombinationen sein können.
Bei den Wellen ist das anders: Es ist mathematisch und damit auch physikalisch möglich, die Summe von Wellenfunktionen zu bilden bzw. aus einer Summe wieder die exakten einzelnen Wellenfunktionen herauszufinden.
Die Überlagerung von zwei Wellen erzeugt eine einzelne Welle. Die Funktion der Überlagerung ist die mathematische Summe der beiden Wellenfunktionen.
Wellen verschiedener Frequenzen können überlagert (summiert) werden, ohne dass die Information der einzelnen Wellen verloren geht. Die nachträgliche Aufteilung in die einzelnen Wellenfunktionen ist jederzeit möglich.
Verstärkung und Auslöschung
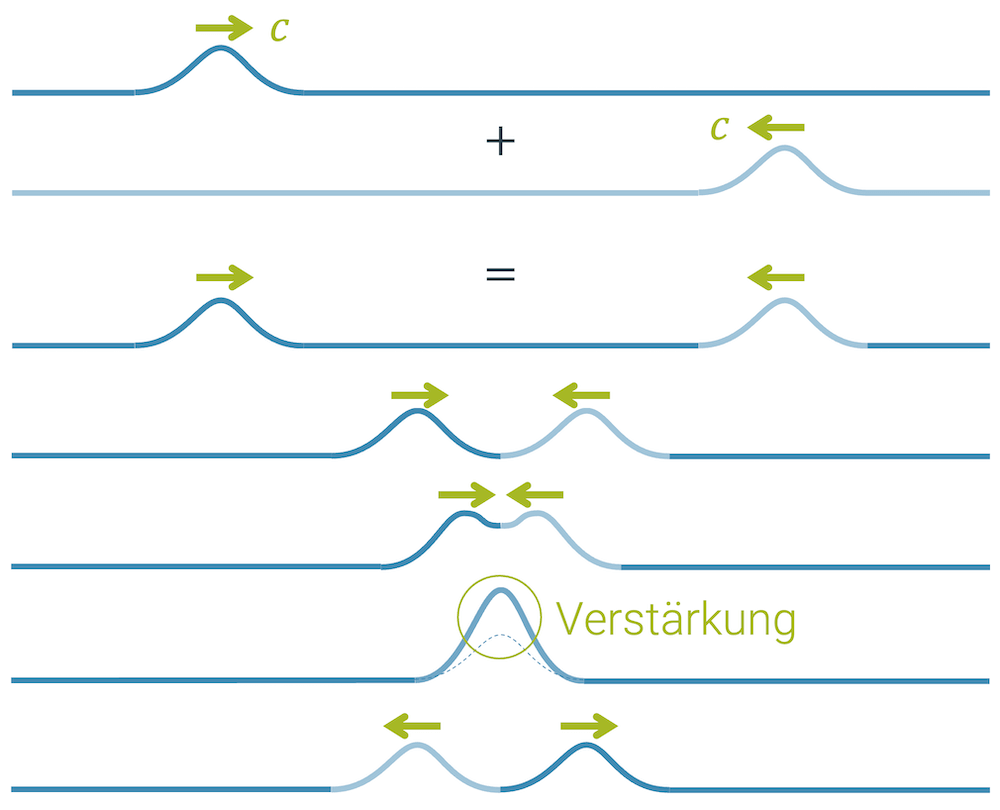
Ein weiterer sehr interessanter Aspekt der Überlagerung von Wellen ist die gegenseitig Verstärkung und v.a. auch Auslöschung. Treffen zwei Wellenberge aufeinander, so werden sie sich kurzzeitig verstärken, ehe sie ungestört ihres Weges weiter gehen werden.
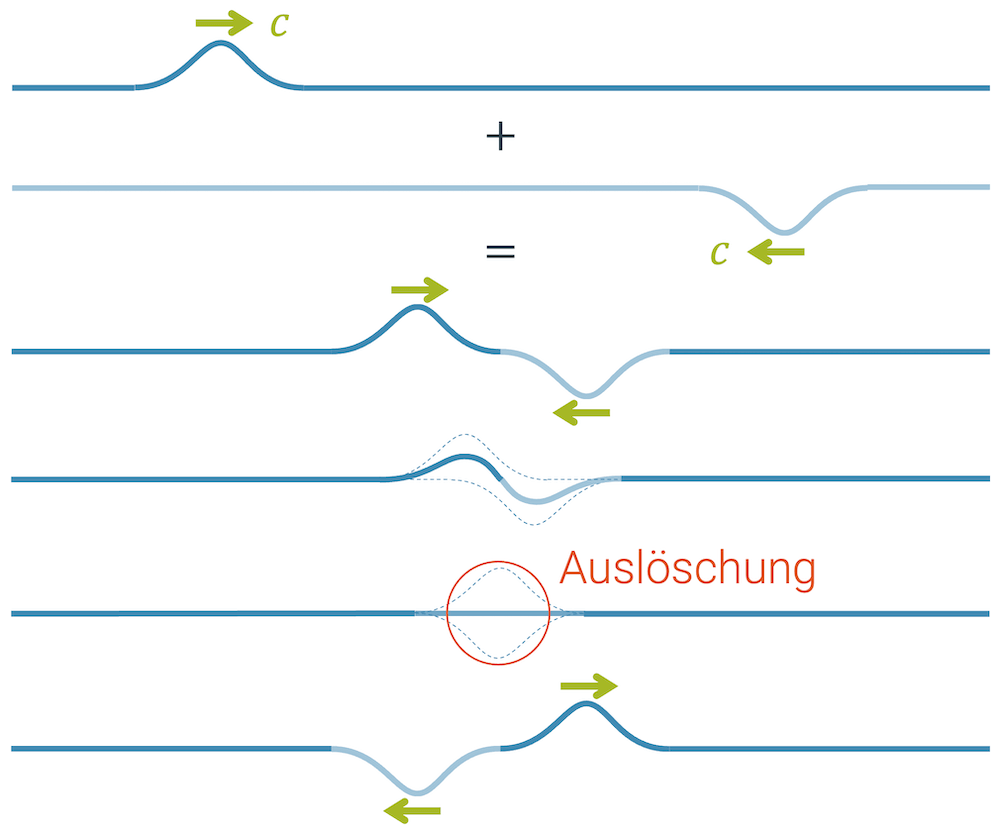
Wenn jetzt aber ein Wellenberg auf ein Wellental auftrifft bzw. zwei Wellenberge mit gleichem Betrag, aber unterschiedlichen Vorzeichen, zusammenkommen, so überlagern sie sich ebenfalls störungsfrei. Jedoch passiert kurzzeitig etwas interessantes: Sie löschen sich gegenseitig auf!
Es ist dieser Effekt, der das faszinierende Phänomen der destruktiven Interferenz erklärt.
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt






Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.