Inhalt
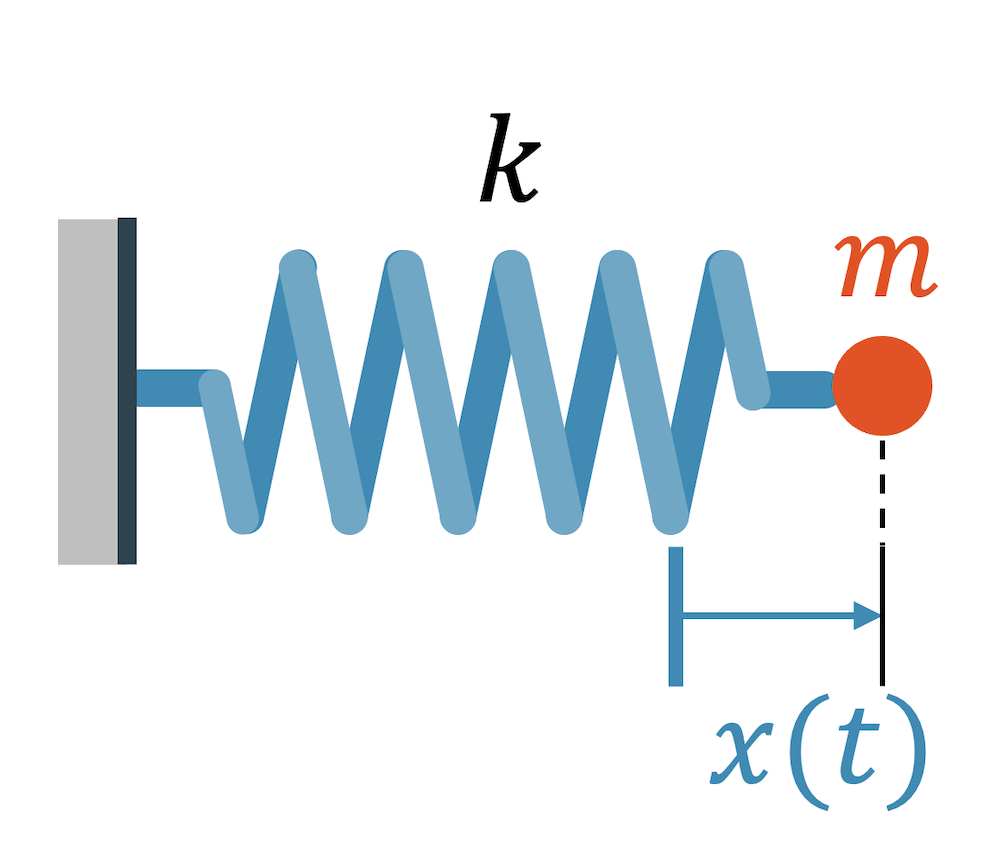
Das Federpendel ist ein Typ eines Schwingungssystems, der sehr oft vorkommt. Jedes Material hat eine gewisse Elastizität. Selbst der armierte Beton einer Brücke deformiert unter Belastung ganz leicht. Sobald diese Belastung wieder weggenommen wird, geht das System zurück in den unbelasteten Zustand, wie eine Feder.
Ein Schwingungssystem dessen Rückstellkraft von einer Feder oder einem elastischen Material kommt, kann mit dem System des Federpendels beschrieben werden.
Die Eigenfrequenz eines solchen Schwingungssystems ist abhängig von der Federkonstanten \(k\) und der Masse \(m\):
\[ \omega_0 = \sqrt{\frac{k}{m}} \]
Um ein schwingendes System zum Schwingen zu bringen, braucht das System einen Input an Energie. Wir können die Masse z.B. um den Abstand \(x=A\) auslenken. Für die Spannung der Feder muss Spannarbeit geleistet werden. Diese Arbeit wird in der Feder in Form von potenzieller Energie gespeichert.
Sobald wir die Masse loslassen, beginnt das System zu schwingen. Die Federkraft beschleunigt die Masse zurück, potenzielle Energie wird abgebaut und zu kinetischer Energie umgewandelt. Wegen ihrer Trägheit schwingt die Masse über die Lage der ungespannten Feder hinaus und benutzt ihre kinetische Energie, um Spannarbeit zu leisten und die Feder zu stauchen. Sobald die Masse die Auslenkung \(-A\) erreicht hat, verharrt sie kurz in Ruhe und der Ablauf beginnt wieder von Neuem.
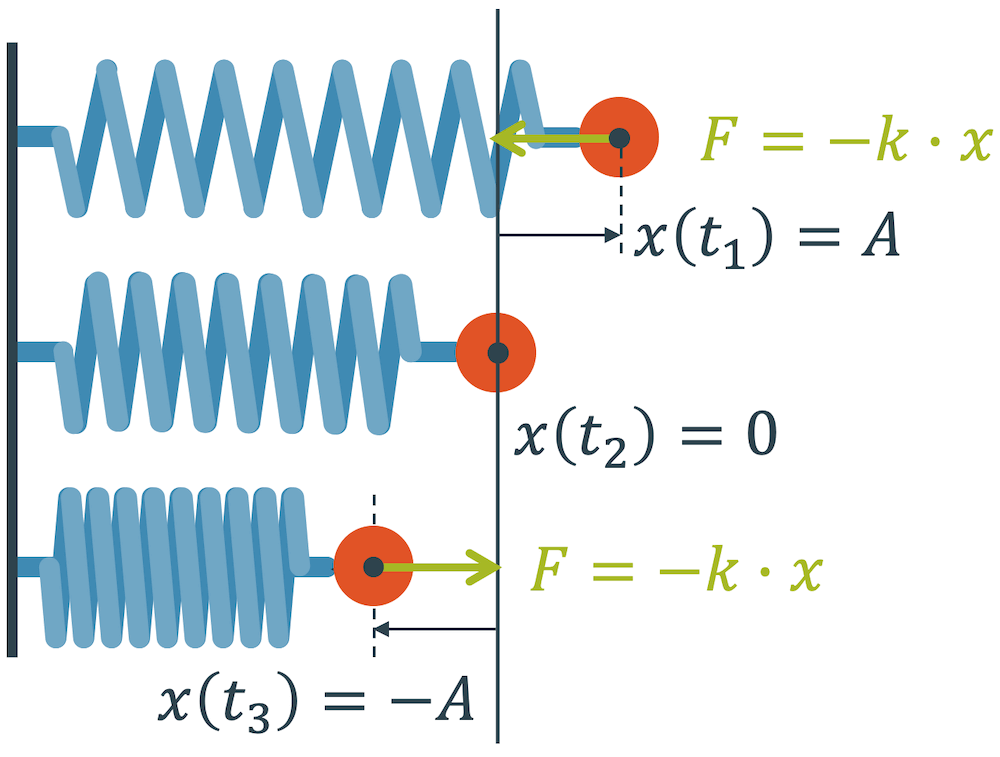
Herleitung der Schwingungsfunktion
Elastische Systeme können bei nicht zu grossen Belastungen mit dem Hooke’schen Gesetz modelliert werden. Gemäss diesem Gesetz ist die Kraft proportional zur Auslenkung gegenüber der unbelasteten Position.
\[ F = -k \cdot x \]
Mit dem Minus-Zeichen wird darauf hingewiesen, dass der Vektor der Kraft \(\vec{F}\) entgegen der Auslenkung \(\vec{x}\) gerichtet ist. Für das Schwingsystem ist es natürlich die Rückstellkraft.
Wenn die Position der Masse \(m\) mit der Funktion \(x(t)\) beschrieben wird, dann ist die erste zeitliche Ableitung, d.h. \(\dot{x}(t)\) die Geschwindigkeit und die zweite zeitliche Ableitung \(\ddot{x}(t)\) entspricht der Beschleunigung. Da es die Federkraft ist, die die Masse beschleunigt, schreiben wir:
\[ F = m \cdot a = m \cdot \ddot{x}(t) = -k \cdot x(t) \]
Damit erhalten wir die Differentialgleichung:
\[ m \cdot \ddot{x}(t) = -k \cdot x(t) \]
Dividiert durch die Masse \(m\) erhalten wir:
\[ \ddot{x}(t) = -\frac{k}{m} \cdot x(t) \]
Mit der harmonischen Schwingung \(x(t)=A \cdot \sin(\omega_0 t)\) erfüllen wir diese Differentialgleichung.
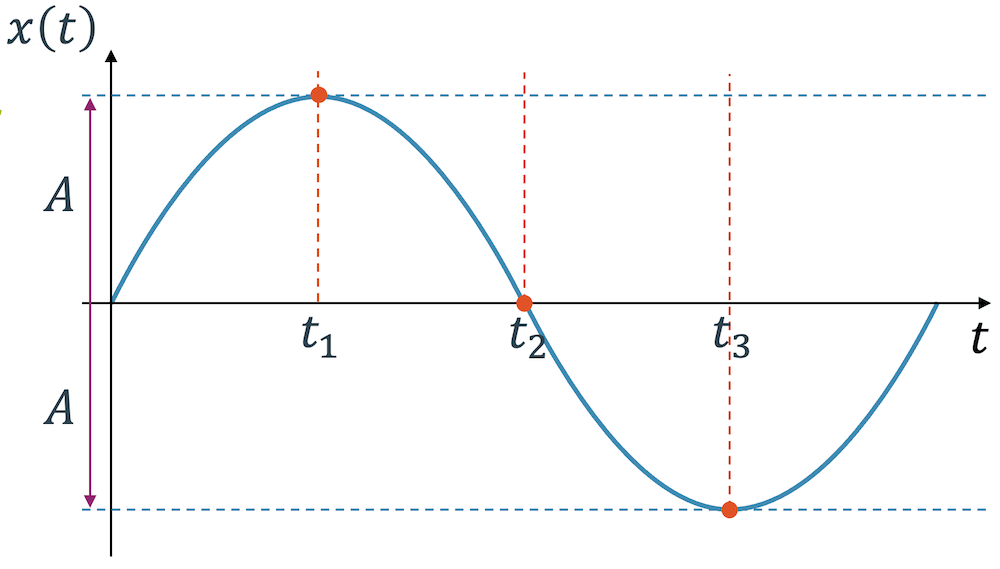
Die Eigenfrequenz \(\omega_0\) entspricht:
\[ \omega_0 = \sqrt{\frac{k}{m}} \]
Je steifer die Feder oder das Material ist, desto höher ist die Eigenfrequenz. Die Masse spielt hier auch eine Rolle. Je grösser die Masse \(m\), desto träger ist das Schwingsystem, was die Eigenfrequenz kleiner macht. Nur steife und sehr leichte Materialien können sehr gut sehr schnell schwingen. Weichere und schwerere Materialien schwingen langsam.
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt






Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.