Inhalt

Erzwungene Schwingung beim Geigenbogen
Die Saiten der Geige werden mit dem Geigenbogen in Schwingung gebracht. Auf dem Bogen gespannt sind Haare, die unter dem Mikroskop eine deutlich erkennbare Schuppenstruktur aufweisen.
Diese Schuppen ragen etwas heraus, ein bisschen wie ein Sägeblatt, d.h. wenn der Bogen über die Saite gestrichen wird, nimmt dieser die Saite ein Stückchen mit und spannt die Saite dadurch.
Irgendwann wird die Rückstellkraft der Saite jedoch zu gross und die Saite spickt zurück, bis sie wieder vom Bogen aufgefangen und auf ein Neues gespannt wird.
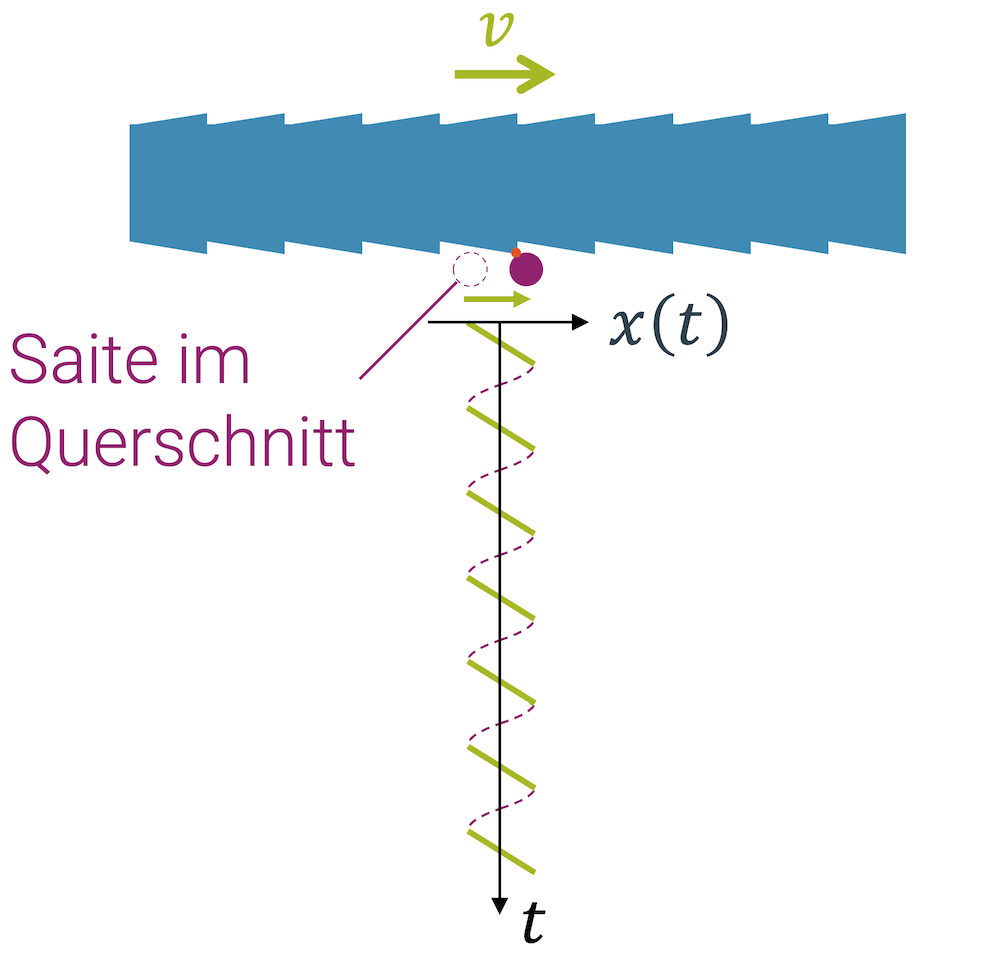
Der Bogen zieht die Saite mit, bis die Saitenkraft für den Bogen zu gross wird.
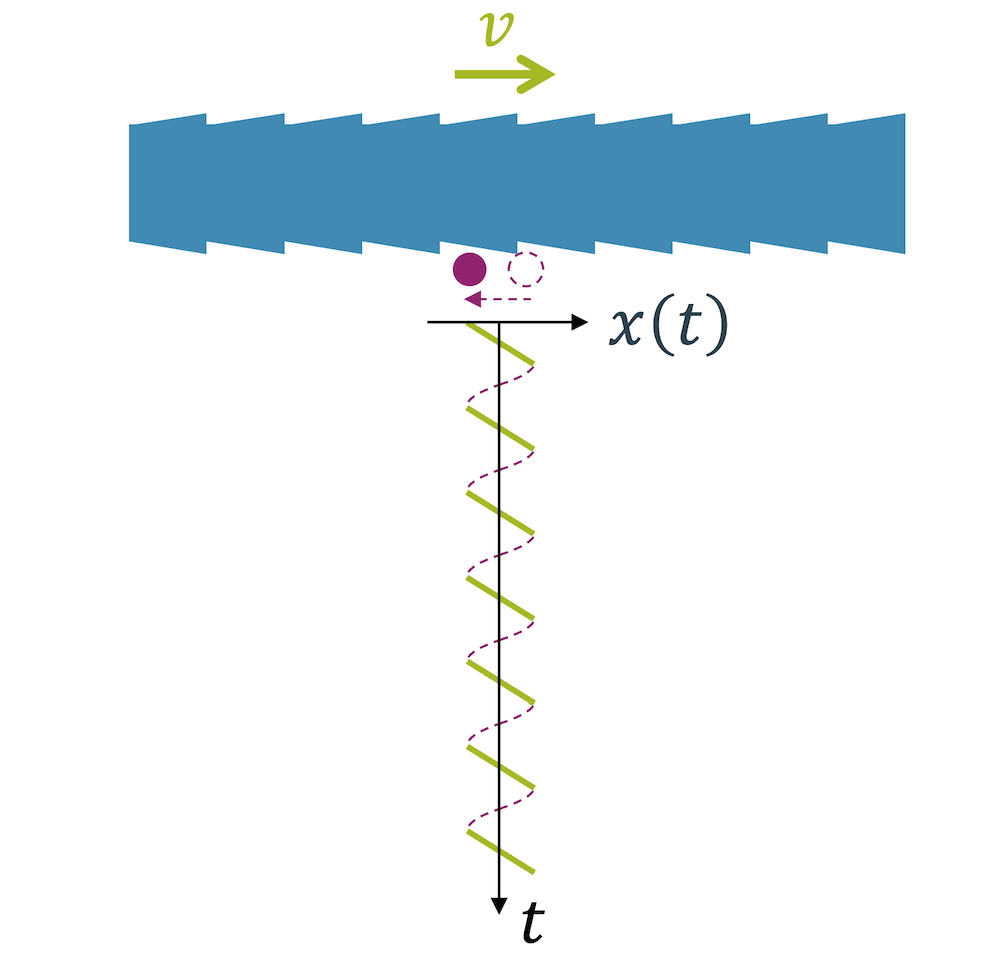
Der Bogen bringt die Saite in Schwingung, indem er sie mit einer anderen Schwingung anregt. Es handelt sich also um zwei Schwingungen: die Anregungsschwingung und die Systemschwingung.
Die Anregungsschwingung hat die sog. Anregungsfrequenz \(\omega_A\). Das System schwingt aber nicht mit dieser Frequenz, sondern versucht mit der Eigenfrequenz \(\omega_0\) zu schwingen.
Wenn ein schwingfähiges System mit Eigenfrequenz \(\omega_0\) durch eine andere Schwingung mit Anregungsfrequenz \(\omega_A\) angeregt wird, reden wir von einer erzwungenen Schwingung.
Resonanz
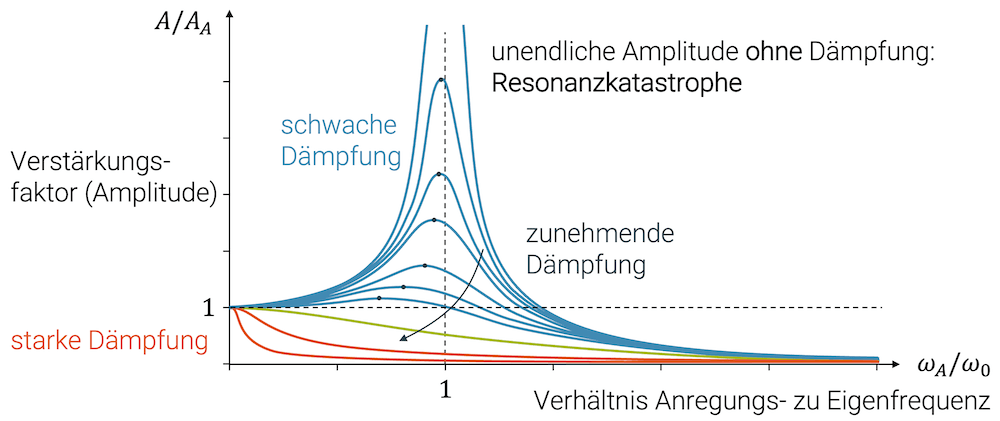
Die Art, wie sich ein schwingfähiges System bei einer erzwungenen Schwingung verhält, ist im folgenden Diagramm zusammengefasst: In der Vertikalen haben wir den Verstärkungsfaktor der sich auf die Amplitude der Schwingung auswirkt. In der Horizontalen ist die Anregungsfrequenz \(\omega_A\) aufgezeichnet bzw. deren Verhältnis im Vergleich zur Eigenfrequenz \(\omega_0\).
Uns fällt sofort auf, dass etwas “dramatisches” passiert, wenn \(\frac{\omega_A}{\omega_0}=1\), d.h. wenn beide Frequenzen gleich gross sind. Bei schwacher Dämpfung kommt ein System in die sog. Resonanz. Bei sehr kleiner Dämpfung kommt es gar zur Resonanzkatastrophe!
Für Bauingenieure ist Resonanz in den meisten Fällen tatsächlich eine Katastrophe. Im Jahr 1940 kollabierte die Hängebrücke Tacoma Narrows Bridge im Staat Washington. Gerade mal vier Monate nach ihrer Fertigstellung regten sehr starke Winde die Brücke mit einer Anregungsfrequenz \(\omega_A\) an, die gleich oder fast gleich der Eigenfrequenz \(\omega_0\) der Brücke entsprach.
Mangelnde Dämpfung führte dazu, dass die Amplitude der Schwingung immer grösser wurde und die Brücke immer stärker ins Schwingen kam, bis gewisse Tragseile rissen und die ganze Brücke auseinanderfiel.
Bei Musikinstrumenten ist die Resonanz meistens ein gewünschter Zustand, weil die Schwingungen der Saite die dünnen Holzwände des sog. Resonanzkörpers des Saiteninstruments ins Schwingen bringen. Diese Schwingungen erzeugen den vollen Klang, den wir von so einem Instrument erwarten.
Ist die Anregungsfrequenz \(\omega_A\) (deutlich) kleiner als die Eigenfrequenz \(\omega_0\), d.h. wenn \(\frac{\omega_A}{\omega_0} < 1\), dann ist der Faktor der Verstärkung der Amplitude näherungsweise 1, d.h. das System schwingt, aber mit der Amplitude der Anregung.
Wir können uns das bei einer Kinderschaukel veranschaulichen. Normalerweise stösst der Erwachsene das Kind mit der Eigenfrequenz an, so dass die Schaukel immer grössere Ausschläge macht (gewollte Resonanz). Wenn der Erwachsene aber viel zu langsam anstossen sollte, dann würde das Kind lediglich zusammen mit der Anregung “schwingen”.
Im anderen Fall, wenn die Anregungsfrequenz \(\omega_A\) (deutlich) grösser als die Eigenfrequenz \(\omega_0\) ist, d.h. wenn \(\frac{\omega_A}{\omega_0} > 1\), dann ist das ein viel zu schnelles Hin- und Her, so dass die Schaukel gar nicht “in die Gänge” kommt. Jede Eigenschwingung wird durch die darauffolgende Anregung wieder zunichte gemacht. Die Amplitude geht gegen null.
Resonanz entsteht, wenn ein schwingfähiges System mit (Eigenfrequenz \(\omega_0\)) mit einer Schwingung angeregt wird (Anregungsfrequenz \(\omega_A\)) und beide Frequenzen (fast) gleich sind und die Dämpfung sehr schwach ist.
Mit jeder Anregung wird ein kleiner Energiebetrag dem System zugeführt, zusätzlich ist das aber ein Betrag zum richtigen Zeitpunkt (Frequenz) und in die richtige Richtung, so dass das System sich aufschaukelt und die Amplitude immer grösser wird.
Die Dämpfung spielt bei der Resonanz eine ganz wichtige Rolle. Je stärker sie ins Gewicht fällt, desto schneller wird Energie wieder aus dem System genommen, indem sie in Wärme umgewandelt wird. Die kritische Dämpfung ist die Grenze, ab welcher das System gar nicht mehr schwingt, sondern nur noch abklingt.
Wenn Resonanz ein Aufschaukeln bzw. Aufsummieren von kleinen Energiebeträgen ist, alle mit einer sich aufsummierenden Wirkung, dann nimmt eine genug grosse Dämpfung genug Energie aus dem System, so dass das System gar nicht aufgeschaukelt werden kann.
Verschiedene Fälle von Anregung
Wir werden jetzt ein paar Beispiele uns anschauen. Im ersten Fall ist die Anregungsfrequenz \(\omega_A\) grösser als die Eigenfrequenz \(\omega_0\). Im Diagramm sind wir rechts der Marke \(\frac{\omega_A}{\omega_0}=1\), weil \(\omega_A > \omega_0\). Die Amplitude der Systemschwingung ist im Vergleich zur Anregungsschwingung schwächer (Abschwächung).
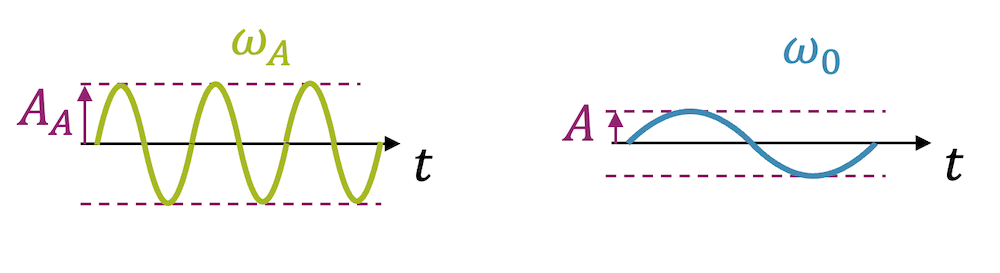
Im zweiten Fall regen wir mit einer Anregungsfrequenz \(\omega_A \approx \omega_0\) an, d.h. wo die Anregungsfrequenz (fast) gleich der Eigenfrequenz des Systems ist. Bei schwacher Dämpfung wird selbst bei kleiner Anregungsamplitude, das System in Resonanz kommen und immer stärker schwingen.
Im Diagramm erkennen wir, dass der Verstärkungsfaktor von der Dämpfung abhängt. Je schwächer die Dämpfung, desto grösser ist die Amplitudenverstärkung.
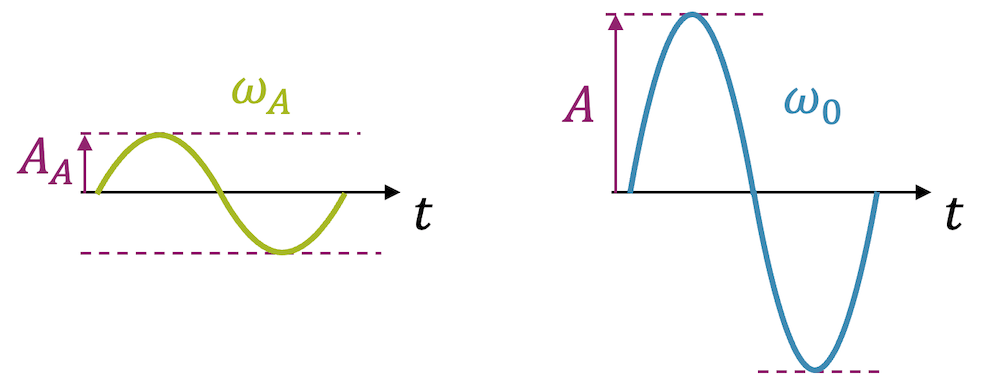
Wenn die Dämpfung sehr stark gewählt wird, wird selbst bei einer Anregung bei der gefährlichen Eigenfrequenz \(\omega_0\) das System von einer Resonanz verschont. Im Diagramm sind wir zwar bei der gefährlichen Frequenz \(\omega_0\), der Verstärkungsfaktor ist aber aufgrund der Dämpfung unterhalb der 1-Marke, d.h. die Amplitude ist kleiner als 1.
Die Dämpfung ist sogar so stark, dass es gar nicht zu einer eigentlichen Schwingung kommt. Das System schlägt etwas aus und kommt dann wieder zurück.
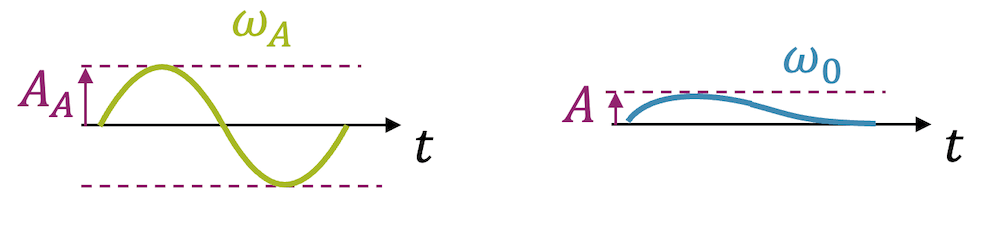
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt






Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.