Inhalt
Das Wichtigste in Kürze
Der Konkavspiegel (Hohlspiegel) kann folgende Bilder erzeugen:
-
- Verkleinertes, umgekehrtes, reelles Bild (bei grosser Gegenstandsweite, \(g>2f\))
-
- Vergrössertes, umgekehrtes, reelles Bild (bei mittlerer Gegenstandsweite, \(g < 2f\))
-
- Verkleinertes, aufrechtes, virtuelles Bild (bei kleiner Gegenstandsweite, \(g<f\))
Videos
Der Konkav- bzw. Hohlspiegel hält wirklich ein paar interessante Überraschungen bereit: Er kann ein vergrösstertes oder verkleinertes, ein reelles oder virtuelles oder ein aufrechtes oder umgekehrtes Bild erschaffen. Das Kriterium ist die Gegenstandsweite im Vergleich zur Brennweite des Spiegels. Der Konkavspiegel ist interessanter und komplexer als der mit ihm verwandte Konvexspiegel.
Das Verständnis über die Entstehung dieser Bilder ist für das Verständnis der Sammellinse sehr wichtig. Die Sammellinse verhält sich nämlich sehr ähnlich zum Konkavspiegel und erzeugt ebenfalls verschiedene Arten von Bildern.
Der Konkavspiegel (Hohlspiegel) kann folgende Bilder erzeugen:
- Verkleinertes, umgekehrtes, reelles Bild (bei grosser Gegenstandsweite, \(g>2f\))
- Vergrössertes, umgekehrtes, reelles Bild (bei mittlerer Gegenstandsweite, \(g < 2f\))
- Verkleinertes, aufrechtes, virtuelles Bild (bei kleiner Gegenstandsweite, \(g<f\))
Reelles, verkleinertes Bild
Bei grossem Abstand (im Vergleich zur Brennweite) entsteht ein verkleinertes, umgekehrtes, reelles Bild. Für die Konstruktion benutzen wir zwei Strahlen von der Kerzenspitze ausgehen: den Parallel- und den Brennpunktstrahl. Gemäss den Regeln der speziellen Strahlen bei gewölbten Spiegeln, wird der Parallelstrahl zu einem Brennpunktstrahl und der Brennpunktstrahl wird zu einem Parallelstrahl.
Die beiden reflektieren Strahlen kreuzen sich in einem Punkt. Das ist der Bildpunkt der Kerzenspitze, denn alle Strahlen der Kerzenspitze (nicht nur die beiden, die wir konstruiert haben) gehen durch diesen Punkt. Würden wir einen Schirm an diese Stelle hinhalten, würde die Kerzenspitze in diesem Punkt abgebildet werden. Beim Punkt handelt es sich natürlich um einen reellen Bildpunkt, also ist das Bild tatsächlich reell.
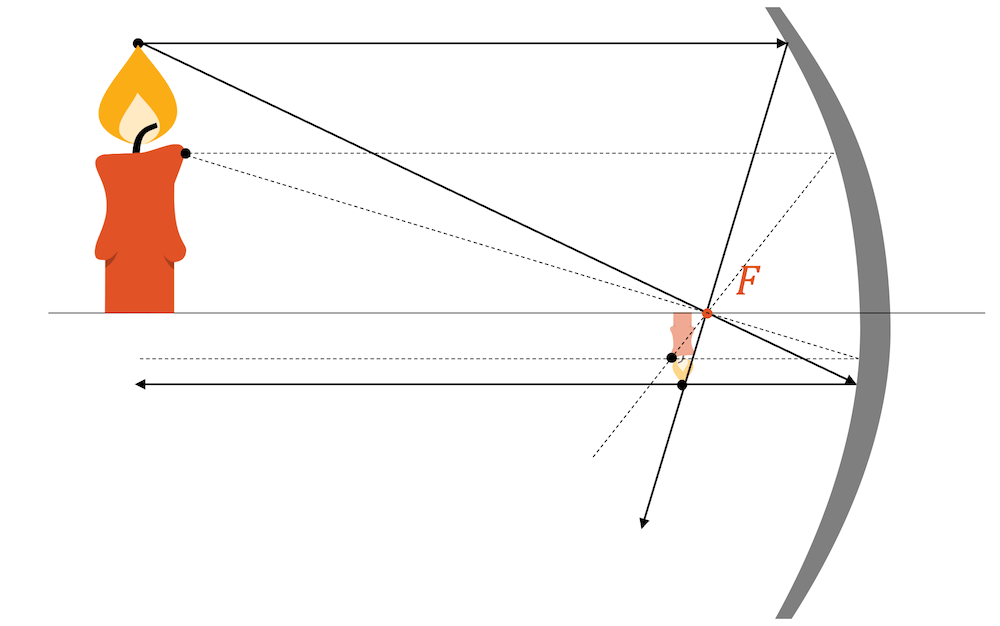
Eigentlich reicht die Konstruktion von zwei Strahlen der Kerzenspitze um den Bildpunkt der Kerzenspitze zu erhalten. Wir können dann annehmen, dass das Bild so platziert ist, dass die Kerzenspitze in diesen Punkt kommt. Wir haben hier am Beispiel eines Punktes des Kerzenkörpers aufgezeichnet, dass die Strahlen von diesem Punkt aus ebenfalls in einem Bildpunkt zusammenkommen. Dieser Bildpunkt bestätigt, dass das Bild eine kleine umgekehrte Kerze ist.
Reelles, vergrössertes Bild
Schieben wir den Gegenstand relativ nahe an den Brennpunkt heran, so erhalten wir mit der gleichen Konstruktion der beiden Strahlen einen Bildpunkt, der weiter vom Spiegel entfernt ist. Das Bild der Kerze ist auch dieses Mal umgekehrt und reell. Allerdings ist das Bild dieses Mal grösser als die richtige Kerze.
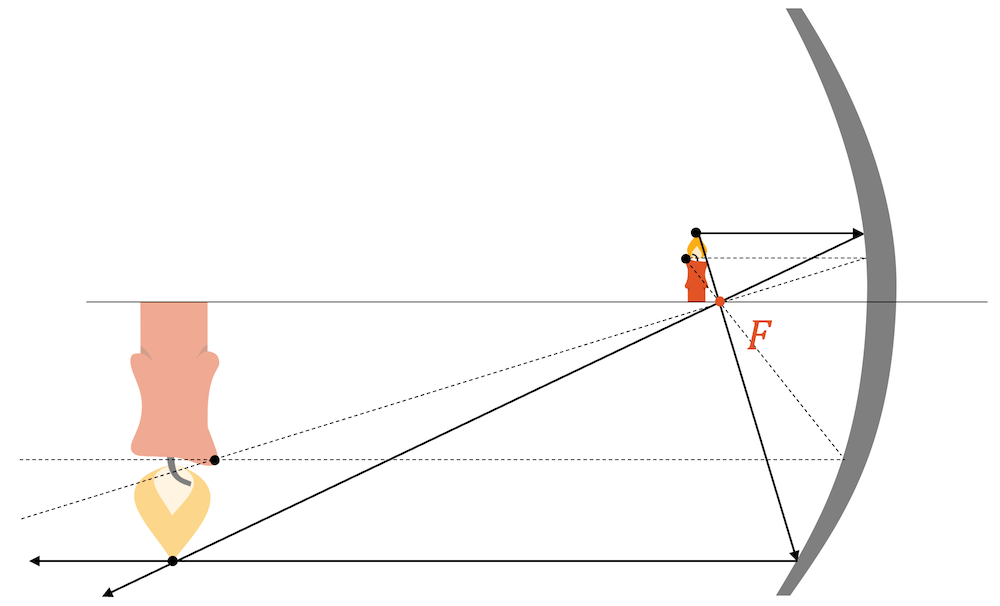
Virtuelles Bild
Schieben wir die Kerze noch näher an den Spiegel heran, so entsteht ein aufrechtes Bild, das dieses Mal aber hinter dem Spiegel ist, d.h. es muss virtuell sein, weil die Lichtstrahlen gar nicht hinter den Spiegel gelangen können.
Für die Konstruktion nehmen wir wieder den Parallel- und den Brennpunktstrahl der Kerzenspitze.
Der Brennpunktstrahl geht gar nicht durch den Brennpunkt, sondern verläuft so, als käme er vom Brennpunkt. Tatsächlich wurde er ja von der Kerzenspitze abgegeben. Die Verlängerung vom Brennpunkt zeigt, dass der Strahl für einen Betrachter den gleichen Verlauf hat, wie ein Brennpunktstrahl. Nach dem Spiegel wird dieser Strahl zu einem Parallelstrahl.
Der Parallelstrahl kann ganz normal konstruiert werden, indem er nach dem Spiegel durch den Brennpunkt verläuft.
Die beiden neu konstruierten Strahlen verlaufen vom Spiegel weg, jedoch verlaufen sie auseinander, d.h. sie werden sich sicherlich nicht in einem Bildpunkt kreuzen. Die Bildung eines reellen Bildpunkts ist ausgeschlossen und deshalb wird auch kein reelles Bild erschaffen werden.
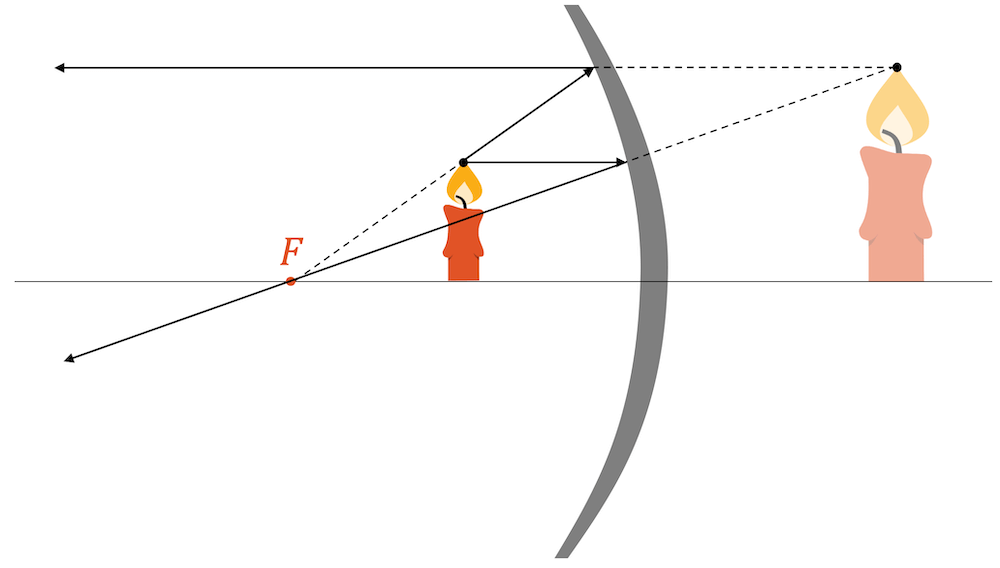
Die auseinander laufenden Strahlen kreuzen sich in einem Bildpunkt, allerdings ist dieser hinter dem Spiegel. Wir konstruieren deshalb die Verlängerung der Strahlen hinter den Spiegel. Für einen Betrachter der beiden Lichtstrahlen kommen beide ja aus dem gleichen Punkt heraus, denn der Betrachter nimmt immer an, dass Strahlen geradlinig verlaufen. Der Punkt ist ein scheinbarer Bildpunkt oder eben, ein virtueller Bildpunkt unserer Kerzenspitze. Wir setzen die Kerze ein und fertig ist das virtuelle, aufrechte und vergrösserte Bild der Kerze.
Zu Überprüfung könnten wir einen zweiten Punkt der Kerze abbilden und würden die Bestätigung erhalten, dass das virtuelle Bild tatsächlich so hinter dem Konkavspiegel steht.
Verschiedene Bilder bei Konkavspiegeln: Übersicht
Die verschiedenen Bildarten sind am Anfang etwas verwirrend. Die folgende Grafik soll hier etwas mehr Übersicht geben:
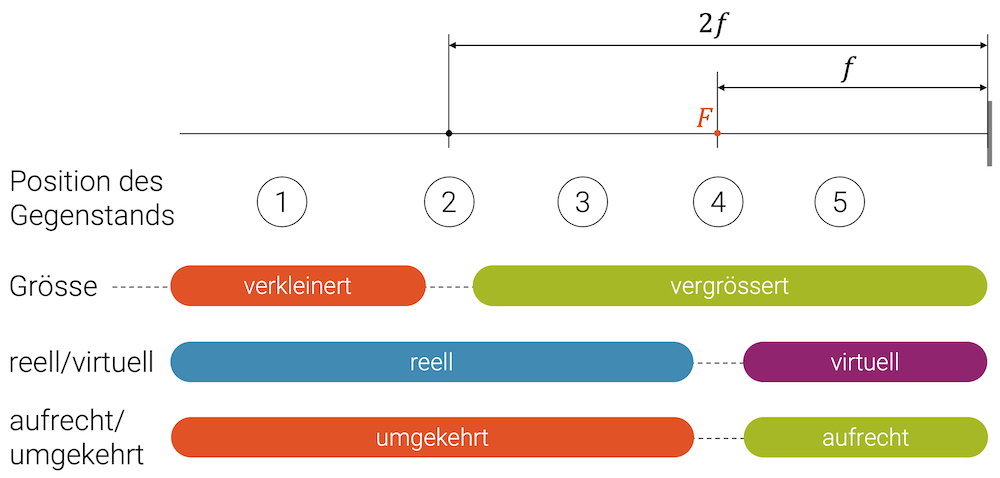
- Position 1: Ganz links in der Grafik haben wir die Positionen 1 in welcher der Gegenstand noch weit vom Spiegel (ganz rechts) ist. Es entsteht ein verkleinertes, reelles und umgekehrtes Bild, genauso wie wir es weiter oben im ersten Beispiel gesehen haben.
- Position 2: In dieser Position ist das Bild immer noch reell und umgekehrt. Allerdings befindet sich das Bild am gleichen Ort wie der Gegenstand, d.h. \(b = g\). Mit Hilfe des Strahlensatzes der Optik erhalten wir: \(B=G\), d.h. das Bild ist genau gleich gross wie der Gegenstand.
- Position 3: Diese Situation entspricht unserem zweiten Beispiel, das wir weiter oben besprochen haben. Das Bild ist immer noch reell und umgekehrt, jedoch ist es jetzt weiter vom Spiegel entfernt und deshalb im Vergleich zum Gegenstand vergrössert.
- Position 4: In der Position 4 entsteht etwas ganz Spezielles: Wenn wir versuchen die Konstruktion wie im dritten Beispiel auszuführen, erhalten wir zwei Strahlen, die zueinander parallel verlaufen, d.h. sie bilden weder einen reellen Bildpunkt vor dem Spiegel, noch bilden sie einen virtuellen Bildpunkt hinter dem Spiegel: Sie bilden gar keinen Bildpunkt! In dieser Position entsteht kein Bild.
- Position 5: Genug nahe am Spiegel entsteht, wie im dritten Beispiel gezeigt, ein vergrössertes, virtuelles und aufrechtes Bild.
Simulation
Aufgabensammlung
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt








Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.