Inhalt
Videos

Der waagrechte Wurf ist eine eine zusammengesetzte Bewegung, die aus der Überlagerung einer gleichförmigen waagrechten Bewegung und einem freien Fall entsteht. Beispiele für die Bewegung des waagrechten Wurfs finden wir bei Wasserfällen oder Gegenständen, die über die Tischkante rollen etc.
Beachte, dass der waagrechte Wurf die leicht einfachere Form des schrägen Wurfs ist, bei welchem ein senkrechter Wurf statt einem freien Fall zu der waagrechten Bewegung überlagert wird.
Waagrechter Wurf als zusammengesetzte Bewegung
In der nachfolgenden Grafik sind die Geschwindigkeitsvektoren gezeichnet der zwei Bewegungen, die überlagert werden. Die horizontale gleichförmige Bewegung mit konstanter Geschwindigkeit ist mit blauen Vektoren gezeichnet. Der freie Fall aus der Ruhe heraus, ist mit roten Geschwindkeitsvektoren gezeigt.
Überlagern wir die beiden Bewegungen, so addieren sich die blauen und roten Geschwindigkeitsvektoren. Die Summen der Vektoren sind die grünen Geschwindigkeitsvektoren, die die parabelförmige Bewegung ergeben.

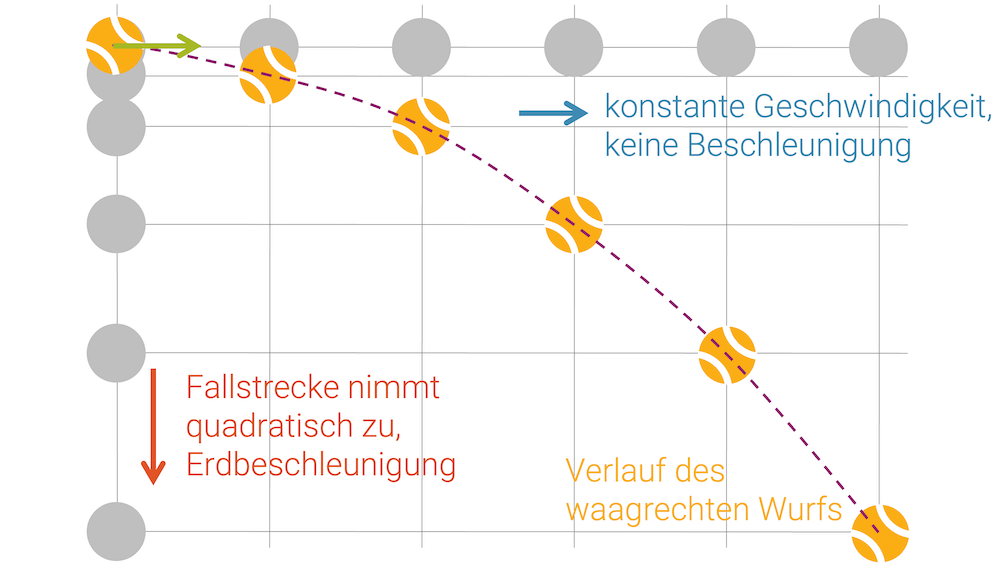
Das Gleiche kann bei einem Tennisball gezeigt werden, der auf einer bestimmten Höhe horizontal abgeschossen wird. Wir stellen uns ein Stroboskoplicht vor, das in regelmässigen Zeitabständen einen Blitz erzeugt und uns die aktuelle Position des Balls verrät. Diese Positionen folgen der waagrechten Wurfparabel, die durch die Überlagerung der beiden Bewegungen konstruiert werden kann.
Einerseits nehmen wir auf der Horizontalen an, dass die Bewegung gleichförmig ist, d.h. mit konstanter Geschwindigkeit erfolgt. Von Blitz zu Blitz verstreicht immer gleich viel Zeit und der Ball kommt auf der Horizontalen somit immer gleich weit. Die horizontalen Abstände sind somit immer gleich lang.
Auf der Vertikalen wird der Ball mit der Erdbeschleunigung beschleunigt, d.h. er hat eine zunehmende Geschwindigkeit gemäss den Regeln des freien Falls. Mit zunehmender Geschwindigkeit werden die Fallstrecken von Blitz zu Blitz immer grösser. Die Position des Balls bzw. dessen Fallstrecke folgt dem Gesetz des freien Falls:
\[ s=\frac{1}{2}gt^2 \]
Kombinieren wir die horizontalen mit den vertikalen Positionen des Balls, erhalten wir die Wurfparabel:
Aufgabensammlung
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt







Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.