Inhalt
Videos

Image by Jumilla
Wenn wir zwei Kräfte \(\vec{F_1}\) und \(\vec{F_2}\) addieren, verschmelzen sie zu einer Summenkraft \(\vec{F_3}\). Dieser Vorgang kann natürlich auch umgekehrt werden:
Wir können zu jeder Kraft \(\vec{F_3}\) zwei Teilkräfte finden, die zusammengezählt, wieder \(\vec{F_3}\) ergeben. Mit Hilfe der beiden Richtungen von \(\vec{F_1}\) und \(\vec{F_2}\) kann um \(\vec{F_3}\) herum ein Parallelogramm konstruiert werden, so dass \(\vec{F_3}\) die Diagonale bildet. Die beiden Seiten des Parallelogramms entsprechen dann \(\vec{F_1}\) und \(\vec{F_2}\), so dass gilt:
\[ \vec{F_1} + \vec{F_2} = \vec{F_3} \]
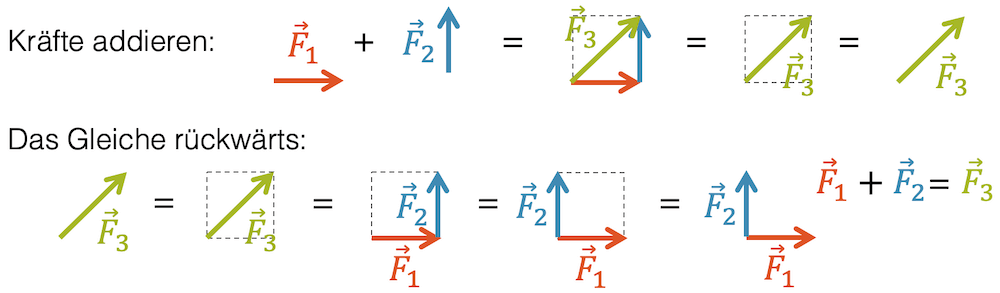
Das Vorgehen ist analog zur Addition. Wir konstruieren zuerst das Parallelogramm, das durch die Richtung der beiden Teilkräfte aufgespannt wird und setzen es um die zu zerlegende Kraft \(\vec{F_3}\) so, dass sie die Diagonale des Parallelogramms bildet. Nun machen wir die zwei Seiten des Parallelogramms zu Teilkräften.
Auch hier erinnern wir uns an die Welt der Zahlen: Die Zahl 6 kann z.B. aufgeteilt werden in 1+5, 2+4 oder 3+3. Es gibt unendlich viele Möglichkeiten, die Summe 6 zu erhalten. Bei den Kräften ist es genau gleich. Irgendwelche Richtungen bringen uns nicht viel. Meistens zerlegen wir die Kraft so, dass die zwei Teilkräfte je eine für uns praktische Richtung haben, z.B. in die \(x\)- und die \(y\)-Richtung.
Beachten Sie, dass auch hier die Kraft \(\vec{F_3}\) in gleicher Art wirkt, wie ihre Zerlegung in zwei Kräfte \(\vec{F_1}\) und \(\vec{F_2}\). Beide Fälle sind wieder physikalisch äquivalent, d.h. der betrachtete Gegenstand oder Körper wird sich in beiden Fällen genau gleich verhalten, egal ob \(\vec{F_1}\) und \(\vec{F_2}\) wirken oder nur \(\vec{F_3}\).
Beispiel
An einem Drachen wirkt die Kraft \(\vec{F_3}\). Zerlegen Sie sie in zwei Kräfte, die Gewichtskraft \(\vec{F_1}\) und die Windkraft \(\vec{F_2}\). Beachten Sie dabei, dass die Gewichtskraft immer senkrecht nach unten zeigt.
Wir müssen zuerst das Parallelogramm zeichnen, mit den folgenden beiden Prämissen:
- Eine Seite des Parallelogramms hat die senkrechte Richtung der Gewichtskraft
- \(\vec{F_3}\) bildet die Diagonale des Parallelogramms
Nachdem wir das Parallelogramm gezeichnet haben, können wir vom Angriffspunkt der Kraft \(\vec{F_3}\) aus die beiden Teilkräfte \(\vec{F_1}\) und \(\vec{F_2}\) zeichnen.
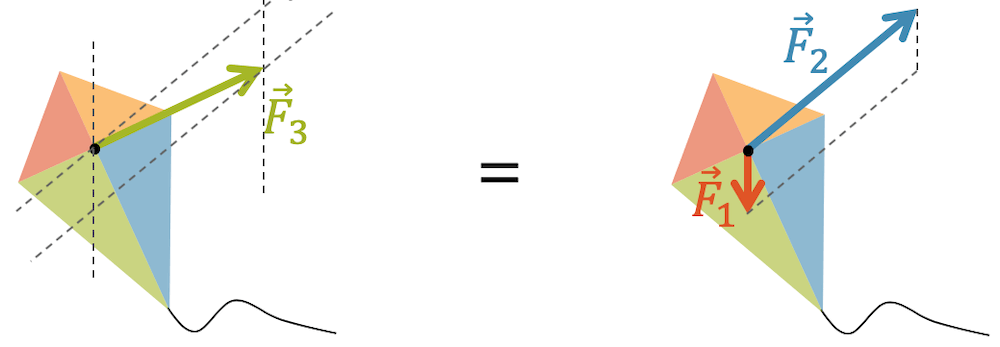
Kraftkomponenten an der schiefen Ebene
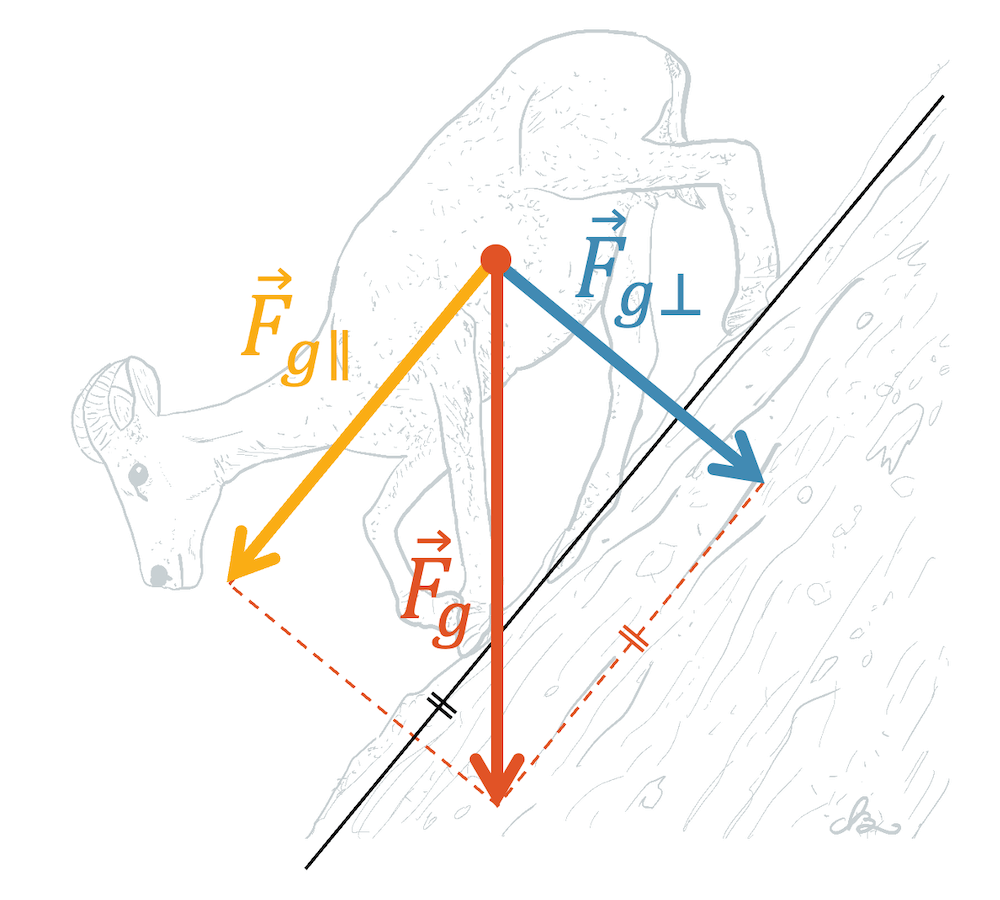
Bei der schiefen Ebene wird die Technik der Zerlegung der Kräfte angewendet, um das Problem zu vereinfachen. Die Gewichtskraft zeigt immer senkrecht nach unten. Wäre die Ebene horizontal, würde die Gewichtskraft damit senkrecht zur Ebene zeigen. Bei der schiefen Ebene, wirkt sie jedoch unter einem bestimmten Winkel.
Es empfiehlt sich nun die Gewichtskraft \(\vec{F_G}\) in zwei Teilkräfte aufzuteilen, einer Teilkraft \(\vec{F_{\parallel}}\) parallel zur Ebene und einer Teilkraft \(\vec{F_{\perp}}\) senkrecht zur Ebene. Wir benutzen hier das Symbol “\)\parallel\)” für parallel und das Symbol “\)\perp\)” für senkrecht.
Als Parallelogramm wählen wir ein Rechteck, so dass \(\vec{F_G}\) die Diagonale bildet. Die Rechteckseiten geben uns jetzt die beiden Teilkräfte, die die Gewichtskraft ersetzen:
\[ \vec{F_G} = \vec{F_∥} + \vec{F_⊥} \]
Die Aufteilung der Gewichtskraft ist für die Interpretation der Situation sehr nützlich: Die Gewichtskraft drückt das Tier mit der senkrechten Komponente \(\vec{F_{\perp}}\) gegen die Felswand. Die parallele Komponente \(\vec{F_{\parallel}}\) zeigt schräg nach unten. Das Tier muss jetzt mit seinen Hufen genügend Halt finden, um \(\vec{F_{\parallel}}\) mit Haftreibung aufzuheben. Je steiler die schiefe Ebene, desto grösser wird der parallele Anteil \(\vec{F_{\parallel}}\) und desto mehr Halt braucht das Tier, um nicht wegzurutschen.
Beachte, dass in gewissen Büchern von einer Hangabtriebskraft die Rede ist. Damit ist nichts anderes als die Parallelkomponente \(\vec{F_{\parallel}}\) der Gewichtskraft \(\vec{F_G}\) gemeint. Die Bezeichnung kann zu Verwirrungen führen, denn sie suggeriert, dass es sich um eine eigenständige Kraft handelt. Wenn Sie diese und die Gewichtskraft nebeneinander stehen haben, zählen Sie etwas doppelt, denn diese Hangabtriebskraft ist ja in der Gewichtskraft schon enthalten.
Aufgabensammlung
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt







Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.