Inhalt
Videos

Die Federkraft ist die Kraft, die es braucht, um eine Feder zu dehnen oder zu stauchen. Gemäss dem Hooke’schen Gesetz ist die Kraft \(F\) proportional zur Längenänderung \(\Delta x\):
\[ F = k \cdot \Delta x \]
Die Proportionalitätskonstante \(k\) (oder \(D\)) ist die Federkonstante. Je härter die Feder, desto grösser ist die Federkonstante.
Die meisten Materialien zeigen bei kleiner Kraft ein elastisches Verhalten, d.h. die Verformung ist gemäss Hooke’schem Gesetz proportional zur eingesetzten Kraft (oder umgekehrt) und sie bildet sich vollständig zurück, sobald keine Kraft mehr wirkt. Die bei der Verformung eingesetzte Spannarbeit ist in Form von potenzieller Energie gespeichert.
Plastisches Verhalten setzt bei grösseren Kräften ein oder bei besonders leicht verformbaren Werkstoffen. Die Verformung bleibt auch nach Entlastung bestehen. Meistens wird sämtliche Spannarbeit in Wärme umgewandelt.
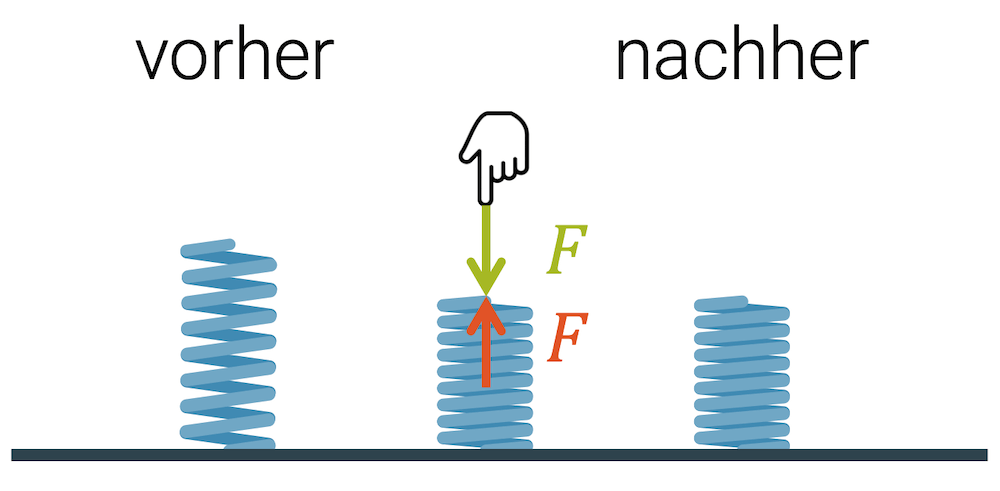
Die Feder kann zusammengedrückt oder auseinander gezogen werden. Die Summe der beiden Kräfte, die an der Feder wirken, ist null, d.h. die beiden Kräfte sind vom Betrag her gleich. Wir haben Kräftegleichgewicht. In der folgenden Skizze sind die beiden Kräfte eingezeichnet, die an der Feder wirken.
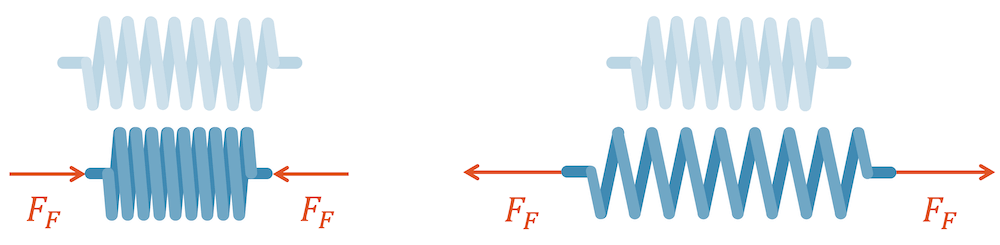
Die Kräfte, mit welcher die Feder auf ihre Umgebung wirkt, sind genau gleich gross, aber entgegengesetzt in der Richtung, d.h. die Feder links möchte sich wieder ausdehnen und wirkt deshalb mit zwei Kräften, die nach aussen zeigen. Die Feder links wirkt mit zwei zusammenlaufenden Kräften.
Hooke’sches Gesetz
Robert Hooke (1635 – 1703) war ein englischer Universalgelehrter, Vermesser und Architekt. Er war massgeblich am Wiederaufbau Londons nach dem Grossbrand von 1666 beteiligt. Er stellte das nach ihm benannte Gesetz auf, wonach die Federkraft \(F\) einfach aus der Längenänderung \(\Delta x\) berechnet werden kann oder umgekehrt.
Hooke bemerkte, dass eine Feder, die mit einer Kraft \(F\) verlängert wird, sich um \(\Delta x\) verlängert. Ziehen wir jedoch mit der doppelten Kraft \(2F\), so ist die Verlängerung der Feder ebenfalls genau doppelt so gross (\(2 \Delta x\)). Bei dreifacher Kraft haben wir die dreifache Längenänderung etc.
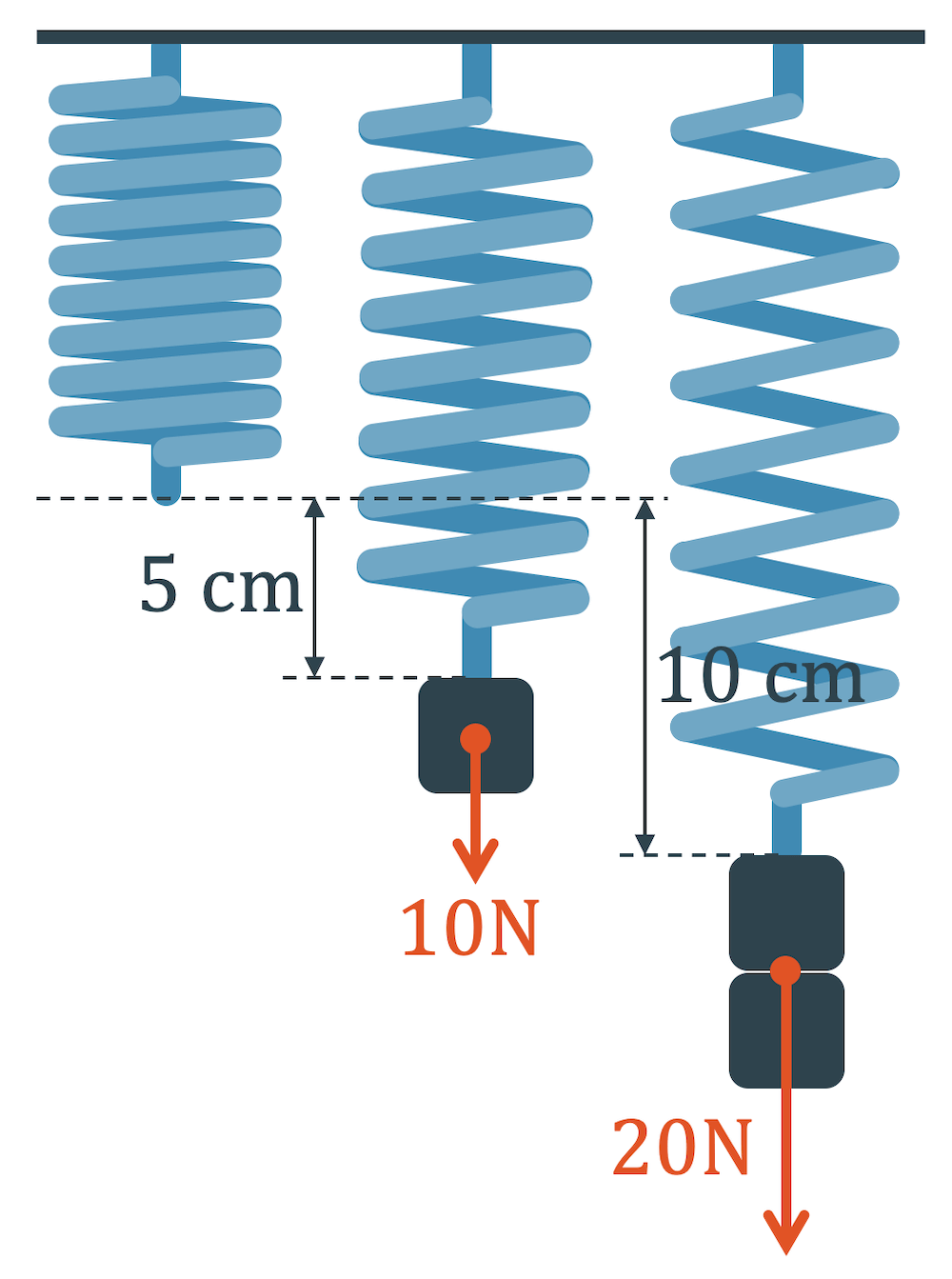
Die Kraft \(F\) ist somit proportional zur Längenänderung \(\Delta x\) oder die Kraft zeigt gegenüber der Längenänderung ein lineares Verhalten. Tragen wir die Kräfte zu den Längenänderungen in einem Kraft-Drehnungsdiagramm ein, liegen die Punkte für eine Feder auf der gleichen Feder-Kennlinie. Diese Linie geht natürlich durch den Ursprung, denn keine Kraft bedeutet natürlich auch keine Längenänderung.
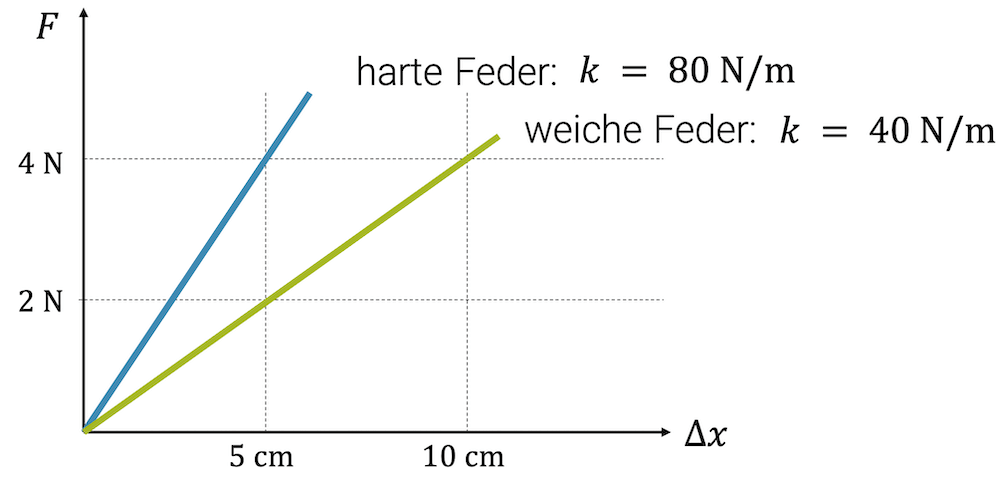
Vergleichen wir eine weiche mit einer harten Feder, so erkennen wir die verschiedenen Steigungen der beiden Geraden. Eine harte Feder wird schon bei einer kleinen Dehnung mit einer grossen Federkraft reagieren, d.h. die Kräfte steigen schnell an und wir haben eine steile Gerade. Eine weiche Feder dehnt sich stark, ohne dass die Kraft allzu sehr zunimmt.
Das Hooke’sche Gesetz setzt die Federkraft \(F\) in Relation zur Längenänderung der Feder \(\Delta x\):
\[ F = k \cdot \Delta x \]
Dabei verbindet der Proportionalitätsfaktor \(k\) die beiden Grössen. Die Grösse \(k\) wird Federkonstante bezeichnet, da sie pro Feder eine konstante Grösse ist. Oft wird auch \(D\) für die Federkonstante verwendet.
Im Diagramm entspricht \(k\) der Steigung der Geraden. Eine Feder, die mit einer Kraft von \(4\) N um 5 cm gedehnt wird, hat eine Federkonstante von
\[ k = \frac{F}{\Delta x} = \frac{4\;\text{N}}{0.05\;\text{m}} = 80\;\frac{\text{N}}{\text{m}} \]
Wenn bei gleicher Ausdehnung die Kraft nur halb so gross ist, beträgt die Federkonstante ebenfalls nur die Hälfte, d.h. \(k = 40\;\frac{\text{N}}{\text{m}}\). Die Grösse der Federkonstante ist gleichzeitig ein Mass für die Härte der Feder.
Beachte, dass das Hookesche Gesetz genau gleich auch für das Zusammendrücken von Federn funktioniert und angewendet wird.
Elastisches Verhalten
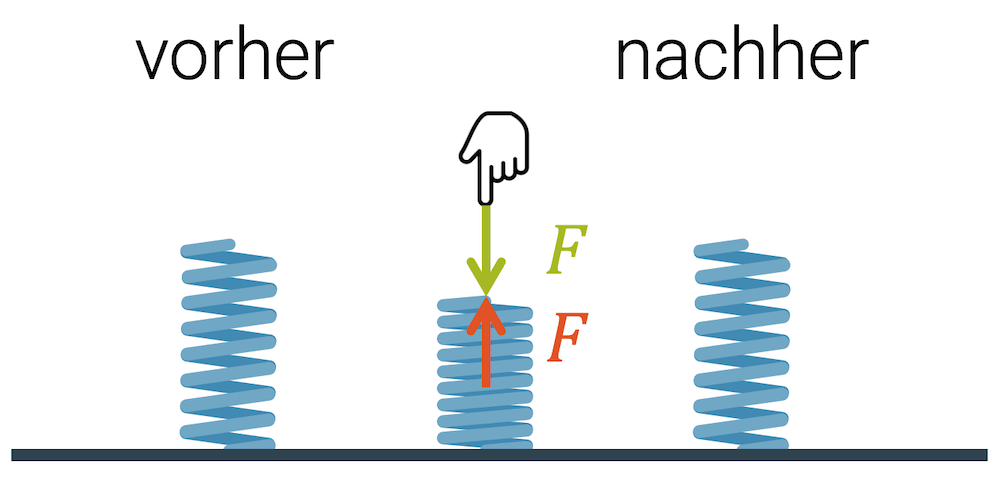
Elastisches Verhalten von Material entspricht dem Verhalten von Federn. Die Kraft ist proportional zur Dehnung oder Stauchung gemäss dem Hookeschen Gesetz. Nimmt man die Kraft wieder weg, verschwindet auch wieder die Längenänderung.
Typische Beispiele sind die Federn, aber auch Gummibänder, Ballone, Putzschwämme etc.
Die meisten Materialien zeigen weitgehend elastisches Verhalten, solange die Kräfte nicht zu gross sind. Auch eine Brücke aus Beton ist weitgehend elastisch und verliert ihre kleine Deformation, sobald die Belastung wieder weggenommen wird. Sie verhält sich wie eine Feder und kann approximativ mit dem Hookeschen Gesetz berechnet werden.
Wird ein elastisches System verformt, so wird die dafür benötigte Arbeit als Spannarbeit am System verrichtet. Die Energie bleibt im Material als potenzielle Energie gespeichert. Im idealen Fall steht sie für eine 100%-ige Rückverformung zur Verfügung.
Plastisches Verhalten
Im Gegensatz zum elastischen Verhalten, ist das plastische Verhalten irreversibel. Nach der Entlastung haben wir eine bleibende Verformung. Energetisch gesehen, steht die Energie nicht mehr für eine Verformung bereit, da sie meistens durch Reibungsarbeit in thermische Energie umgewandelt worden ist.
Typische Beispiele sind Täpfern mit Tonerde, Formgeben bei Alufolie, Knautschzone beim Auto etc.
Metalle, wie die meisten Werkstoffe, sind bei kleinen Belastungen noch elastisch. Übersteigt die Kraft jedoch die Elastizitätsgrenze, so setzt eine irreversible plastische Verformung ein. Wir kennen dieses Verhalten sehr gut aus dem Alltag. Eine Metallfeder kann beliebig oft auseinander gezogen werden. Nach jeder Entlastung zieht sie sich wieder zusammen, als wäre nichts gewesen. Wird sie jedoch überdehnt, weil wir zu stark an ihr ziehen, dann wird sie sich bei Entlastung noch ein bisschen zusammenziehen und eine bleibende Dehnung aufweisen.
Aufgabensammlung
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt







Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.