Inhalt
Das Wichtigste in Kürze
Um ein Objekt anzuheben braucht es Hubarbeit, die in ihm als potenzielle Energie gespeichert wird. Je höher wir das Objekt anheben, umso kleiner wird die Gravitationskraft. Dadurch wird es immer leichter, das Objekt noch höher anzuheben. Pro Meter Höhe kommt immer weniger potenzielle Energie hinzu.
Zeichnen wir die Menge an potenzieller Energie als Funktion des Abstandes von der Erde auf, erhalten wir den typischen Verlauf des Gravitationspotenzials, der die Erdoberfläche als den tiefsten Punkt eines Potenzialtopfs sieht.
Mit Hilfe des Potenzialtopfs verstehen wir, warum das Verlassen der Erde eine gewisse Menge an Hubarbeit (also potenzielle Energie) braucht.
Wir verstehen damit auch, warum beim Herunterfallen, Materie aus dem All diese potenzielle Energie an die Erde abgibt, die wir seit der Entstehung der Erde, heute noch im Erdinnern als thermische Energie vorhanden haben.
Häufigste Fragen
Bedeutung der Hubarbeit im Gravitationsfeld
Wir schauen uns jetzt die potenzielle Energie genauer an. Mit der Hubarbeit ist die physikalische Arbeit beschrieben, die wir aufzuwenden haben, um eine Masse gegen ihre Gewichtskraft auf eine grössere Höhe zu bringen. Bisher haben wir mit einer konstanten Gewichtskraft \(F_g\) gerechnet und können deshalb im F,s-Diagramm die Arbeit \(W\) als Rechteckfläche darstellen.
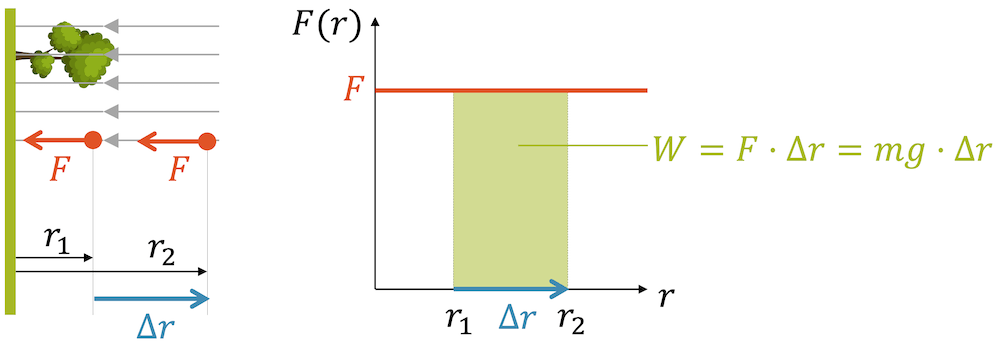
Wenn wir aber in sehr grosse Höhen gehen, dann nimmt die Gravitationskraft immer ein bisschen ab. Die Fläche ist deshalb nicht eine Rechteckfläche, sondern die Fläche unterhalb der Hyperbel, die durch den \(\frac{1}{r^2}\)-Term entsteht. Sie ist kleiner als das Rechteck. Das macht Sinn, denn wenn die Kraft abnimmt, wird es zusehends leichter, die Masse anzuheben und wir brauchen für das gleiche Resultat weniger Arbeit zu leisten.
Mathematisch wird die Sache etwas komplizierter. Um die Fläche unterhalb der Hyperbel und damit die Arbeit zu bestimmen, brauchen wir ein Integral der Kraft über den Weg, den wir abstreichen.
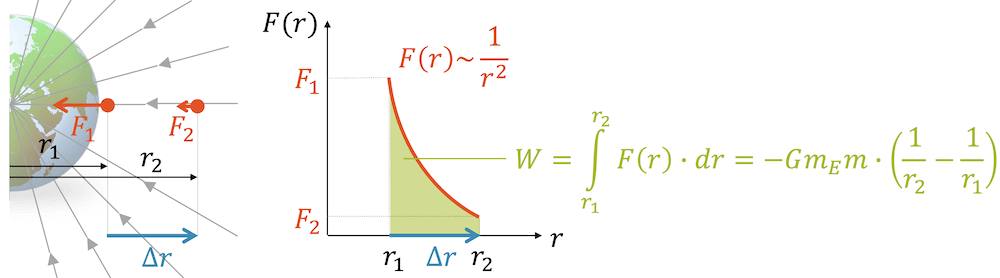
“Je weiter weg wir von der Erde sind, desto flacher wird das Potenzial und umso leichter ist es, noch weiter zu gehen”
Verlauf des Gravitationspotenzials
Wenn wir für jeden Abstand von der Erde wissen, wieviel Arbeit noch benötigt wird, um z.B. einen Meter weiter zu kommen, können wir ein virtuelles Gefälle konstruieren, dem sog. Gravitationspotenzial. Der rote Verlauf im Diagramm zeigt das Potenzial. Es ist die potenzielle Energie bei jedem Abstand \(r\) von der Erde.

Wenn wir ein bisschen von Erde wegkommen möchten, braucht das Hubarbeit und die potenzielle Energie nimmt zu. Am Anfang, nahe zur Erde, ist die Gravitationskraft noch gross und wir brauchen für jeden Meter viel Arbeit. Sind wir aber einmal auf einer gewissen Höhe, so ist die Kraft schon viel kleiner, da sie ja mit dem Quadrat des Abstands abnimmt. Jeder Meter braucht jetzt weniger Anstrengung bzw. weniger Hubarbeit. Es ist, als würden wir einen Hügel hoch laufen, der am Anfang steil war, dann aber immer flacher wird.
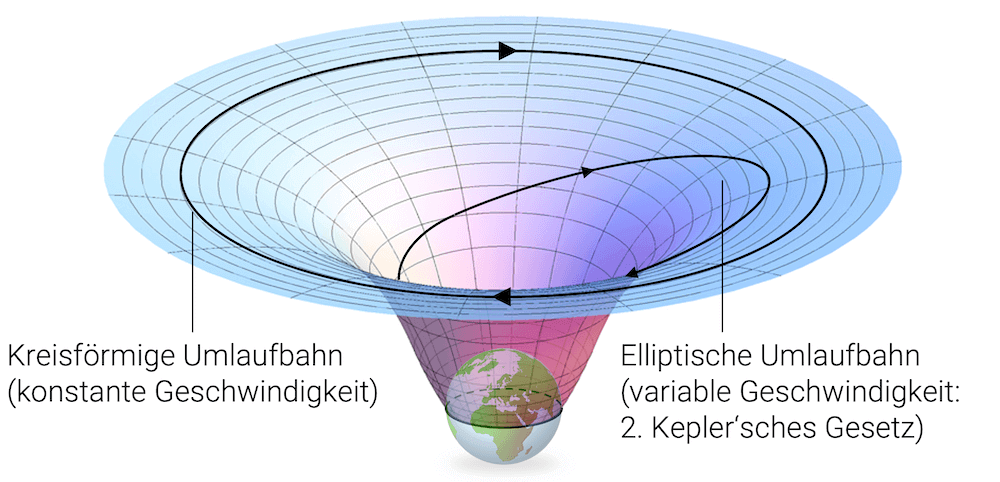
Plot by AllenMcC., licensed under CC BY-SA 3.0, Globe, licensed under CC BY-SA 3.0
“Wer die Energie nicht hat, ist für immer im Topf gefangen!”
Potenzialtopf
Genau so müssen wir uns das Gravitationsfeld der Erde vorstellen. Durch die Gravitationskraft entsteht gewissermassen ein Potenzialtopf mit dem Querschnitt der roten Kurve. Wenn wir aus dem Gravitationsfeld der Erde ausbrechen möchten, müssen wir aus diesem Topf herausklettern und das braucht Hubarbeit bzw. wir brauchen Energie.
Üblicherweise wird das Niveau der potenziellen Energie, das willkürlich festgelegt werden kann, für das Weltraum und die Unendlichkeit auf null gesetzt. Damit ist die potenzielle Energie des Topfs negativ. Die Erde schafft mit ihrer Gravitationskraft gewissermassen eine Absenkung der potenziellen Energie.
Geothermie und Entstehung von Sternen
Beachte, dass Materie, die in den Potenzialtopf hineinfällt, durch die Abnahme der eigenen potenziellen Energie viel kinetische Energie gewinnt, die der Tiefe des Topfs entspricht. Ein Asteroid, der auf die Erde fällt, hat viel kinetische Energie zusätzlich zur kinetischen Energie, die er schon vor dem “Topf” hatte. Beim Aufprall wird die Energie u.a. in Wärme umgewandelt. Bei der Entstehung der Erde hat sich auf diese Art sehr viel Wärme angesammelt, die heute noch im Erdinnern gespeichert ist.
Bei der Entstehung von Sternen ist das genau gleich. Die mit der Gravitationskraft in sich zusammenfallende Materie führt zu einer immer höheren Temperatur, die schliesslich zum “Zünden” der Kernfusion im Kern des Sterns führt.
Aufgabensammlung
Lernziele
- Du weisst, wie Flughöhe und Bahngeschwindigkeit von einander abhängen und kannst die Flughöhe aufgrund einer bestimmten Periode berechnen (Beispiel: geostationäre Satelliten)
- Du kannst mit Hilfe der Formel für die potenzielle Energie im Gravitationsfeld, energetische Betrachtungen machen und diesbezügliche Aufgaben lösen, z.B. die Fluchtgeschwindigkeit bestimmen.
Weitere Links
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt







Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.