Inhalt
Videos
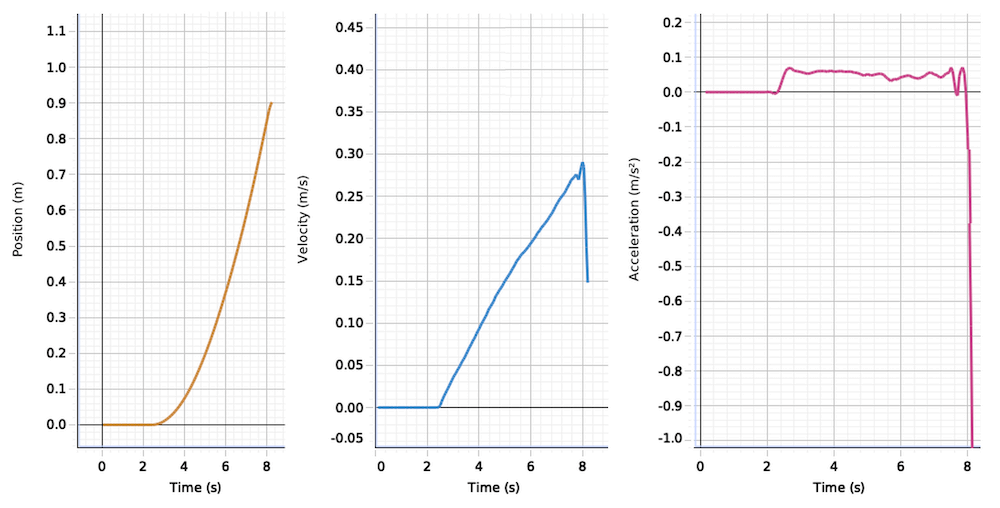
Wird die Geschwindigkeit \(v\) einer Bewegung über die Zeit \(t\) in einem Diagramm aufgetragen, erhalten wir ein v,t-Diagramm. Solche Diagramme werden z.B. durch Fahrtenschreiber für die Überwachung der Ruhezeiten für Berufsfahrer eingesetzt.
Obwohl ein v,t-Diagramm typischerweise Geschwindigkeiten und Zeiten angibt, kann auch eine Strecke herausgelesen werden: Die Fläche zwischen dem Verlauf im v,t-Diagramm und der t-Achse entspricht der gefahrenen Strecke. Die Steigung im v,t-Diagramm ist die Beschleunigung.
Üblicherweise wird die Zeit auf der horizontalen Achse und die momentane Geschwindigkeit \(v\) auf der vertikalen Achse aufgetragen.
Erstellen eines v,t-Diagramms
Ein v,t-Diagramm kann relativ einfach aufgrund eines gegebenen s,t-Diagramms erstellt werden. Um die zeitlichen Abschnitte vom einen auf das andere Diagramm zu übertragen, empfiehlt es sich das v,t-Diagramm unterhalb oder oberhalb des s,t-Diagramms zu zeichnen.
Vorgehen:
- Geeigneten zeitlichen Abschnitt im s,t-Diagramm wählen
- Geschwindigkeit bestimmen (Steigungsdreieck: Steigung ergibt Geschwindigkeit)
- Geschwindigkeit im zeitlichen Abschnitt des v,t-Diagramms auf der richtigen Höhe übertragen
- Wiederholen für die nächsten Abschnitte
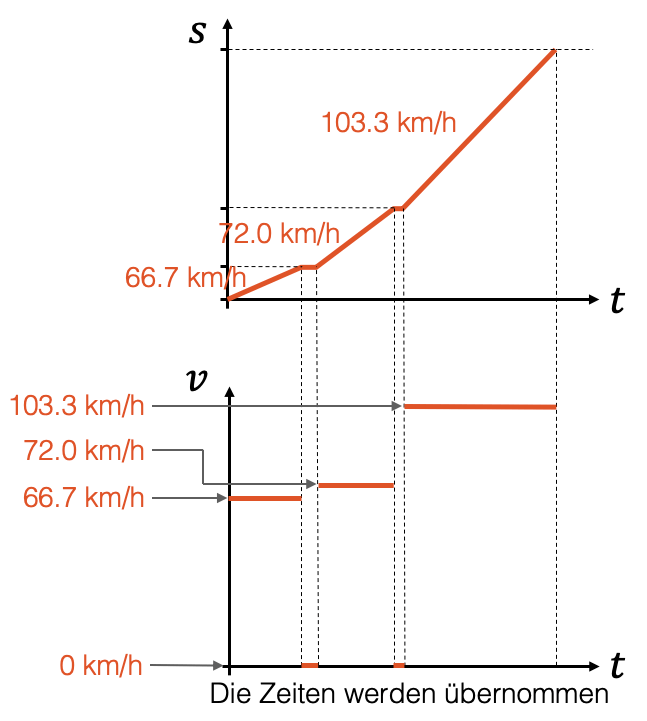
Darstellung einer Position im v,t-Diagramm
Wenn wir in einem v,t-Diagramm eine Rechteckfläche haben, so entspricht sie dem Produkt von \(\Delta t\) und \(\Delta v\):
\[ \Delta t \cdot \Delta v \quad = \quad (t_2-t_1) \cdot (v_2-v_1) \quad = \quad (t_2-t_1) \cdot (\frac{s_2-s_1}{t_2-t_1} – 0) \]
Die Zeiten kürzen sich heraus; die Fläche im v,t-Diagramm ist eine Strecke:
\[ \require{cancel} \Delta t \cdot \Delta v \quad = \quad \cancel{(t_2-t_1)} \cdot \frac{s_2-s_1}{\cancel{t_2-t_1}} \quad = \quad s_2-s_1 \]
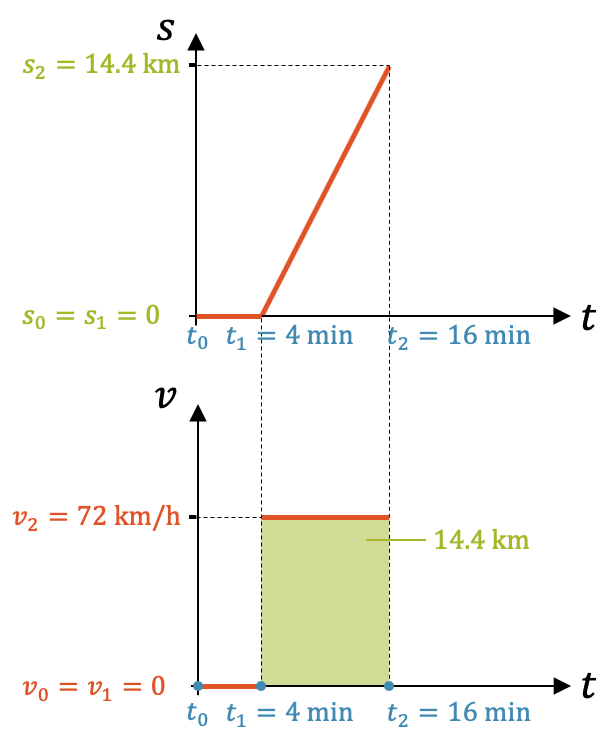
Beispiel
Wie weit kommt ein Zug, der zwischen Minute 4 und 16 mit 72 km/h unterwegs ist?
Im v,t-Diagramm können wir die Fläche als Produkt aufstellen:
\[ \Delta t \cdot \Delta v \quad = \quad (16 – 4)\;\text{min} \cdot (72 – 0)\;\text{km/h} \quad = \quad 12\;\text{min} \cdot 72\;\frac{\text{km}}{\text{h}} \]
Die Einheiten passen nicht. Wir schreiben deshalb die Zeit um, denn 12 min = \(\frac{1}{5}\) h:
\[ \require{cancel} \Delta t \cdot \Delta v \quad = \quad \frac{1}{5}\cancel{\text{h}} \cdot 72\frac{\text{km}}{\cancel{\text{h}}} \quad = \quad \frac{72}{5}\text{km} \quad = \quad 14.4\;\text{km} \]
Aufgabensammlung
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt







Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.