Inhalt
Videos
Wie die Energie oder der noch näher verwandte (translatorische) Impuls, ist auch der Drehimpuls eine wichtige Erhaltungsgrösse der Physik, die uns erlaubt das Verhalten von sich drehenden Körpern besser zu verstehen. Durch die Erhaltung des Drehimpulses bleibt die Rotation des Körpers erhalten.
Wie beim Kraftstoss, der eine Änderung des Impulses bewirkt, verändert ein über eine Zeit lang wirkendes Drehmoment den Drehimpuls.
Der Drehimpuls ist eine Vektorgrösse. Sein Betrag ist definiert als das Produkt von Trägheitsmoment \(I\) und Winkelgeschwindigkeit \(\omega\). Seine Richtung entspricht der Richtung der Drehbewegung:
\[ L = I \cdot \omega \]
Trotz grosser Ähnlichkeit, muss zwischen dem Drehimpuls und der Rotationsenergie unterschieden werden. Analog wird ja auch zwischen dem Impuls und der |kinetischen Energie unterschieden.
Definitionen
Abkürzung: \(\vec{L} \quad\) bzw. \(\quad L\)
Einheit: \([\,L\,] = \frac{\text{kg m}^2}{\text{s}}\)
Der Drehimpuls \(\vec{L}\) ist das Trägheitsmoment multipliziert mit der Winkelgeschwindigkeit. Die Masse des Körpers ist im Trägheitsmoment integriert. Es kommt bei einer Drehbewegung nicht nur darauf an, wie viel Masse der Körper hat, sondern auch wie sie verteilt ist. Dies berücksichtigt das Trägheitsmoment.
Der Drehimpuls ist für die Drehbewegung das analoge Gegenstück zum (translatorischen) Impuls, der dem Produkt von Masse und Geschwindigkeit entspricht.
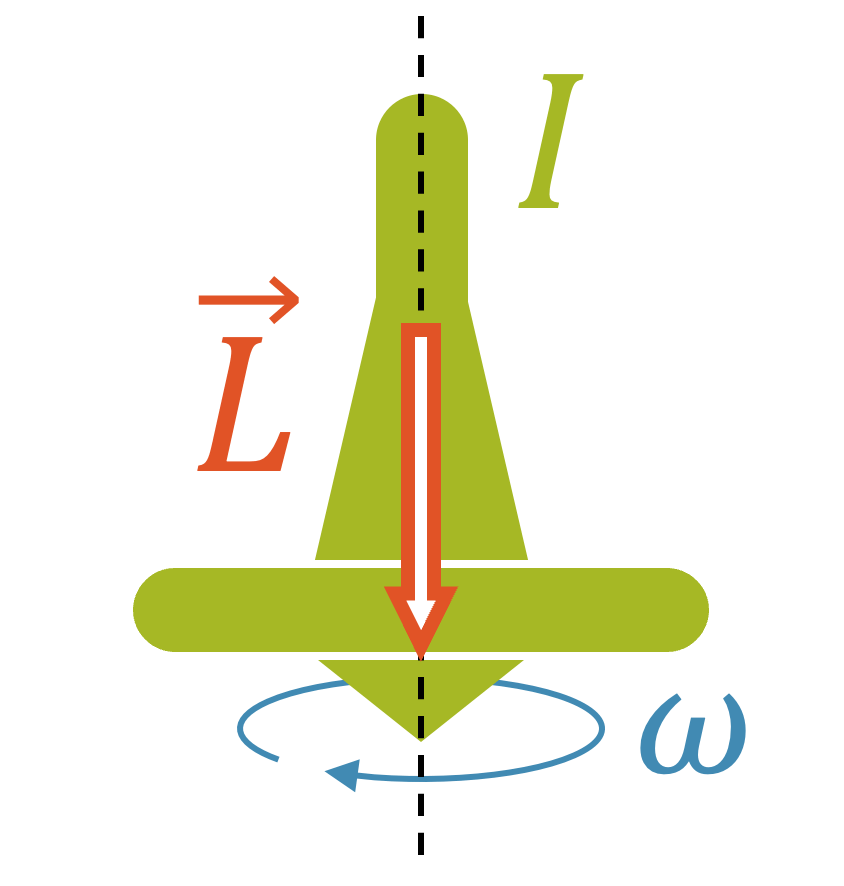
Wie der translatorische Impuls ist auch der Drehimpuls eine Vektorgrösse mit Betrag und Richtung. Die Richtung wird üblicherweise mit einem Doppelpfeil angegeben, der der Rechte-Hand-Regel entspricht. Eine Drehung im Uhrzeigersinn ist ein Pfeil in die Zeichenebene hinein, eine Bewegung im Gegenuhrzeigersinn hat die Richtung aus der Zeichenebene heraus.
Änderung des Drehimpulses durch Drehmoment
Beim translatorischen Impuls hatte wir beim Kraftstoss festgestellt, dass eine Kraftwirkung \(F\) über eine Zeit \(\Delta t\) zu einer Änderung des Impuls \(\Delta p\) führte:
\[ \Delta p = F \cdot \Delta t \]
Für den Drehimpuls haben wir das Analogon mit dem Drehmoment. Wirkt ein Drehmoment \(M\) eine gewisse Zeit \(\Delta t\) an einem System, so ändert sich der Drehimpuls um \(\Delta L\):
\[ \Delta L = M \cdot \Delta t \]
Möchten wir etwas in Rotation versetzen, müssen wir ein Drehmoment eine gewisse Zeit lang wirken lassen. Entscheidend ist hier natürlich die resultierende Kraft und auch das resultierende Drehmoment.
Erhaltung des Drehimpulses
Wie der Impuls und die Energie, ist auch der Drehimpuls eine Erhaltungsgrösse, d.h. der Drehimpuls kann weder erzeugt, noch vernichtet werden. Er ist da und war schon immer da und kann nur weitergegeben werden. Wenn wir ein System haben, das keinen Drehimpuls mit seiner Umgebung austauscht, dann bleibt der Drehimpuls des Systems konstant.
Sehr schön lässt sich die Drehimpulserhaltung bei der Pirouette zeigen. Je nach Figur ist das Trägheitsmoment ein anderes. Wenn die Massen weit von der Drehachse entfernt sind, wie in der Figur links, dann ist das Trägheitsmoment \(I\) gross. Multipliziert mit einer relativ kleinen Winkelgeschwindigkeit \(\omega\) erhalten wir den Drehimpuls \(L_0\).

Geht die Eiskunstläuferin in die Hocke, verändert sie das Trägheitsmoment. Die Massen sind jetzt näher zur Drehachse und somit ist das Trägheitsmoment \(I\) deutlich kleiner als vorher. Der Drehimpuls muss aber erhalten und auf dem Niveau \(L_0\) bleiben. Über die Schlittschuhe kann praktisch nichts mit der Umgebung ausgetauscht werden. Die Eiskunstläuferin ist ein quasi isoliertes System. Um den Drehimpuls bei \(L_0\) aufrecht zu erhalten, muss bei kleiner werdendem Trägheitsmoment die Winkelgeschwindigkeit erhöht werden. Tatsächlich dreht sich die Eiskunstläuferin jetzt deutlich schneller als vorher.
Schliesslich nimmt sie ihre Arme ganz nahe an den Körper und erreicht in aufrechter Stellung das minimal mögliche Trägheitsmoment und damit die maximale Winkelgeschwindigkeit.
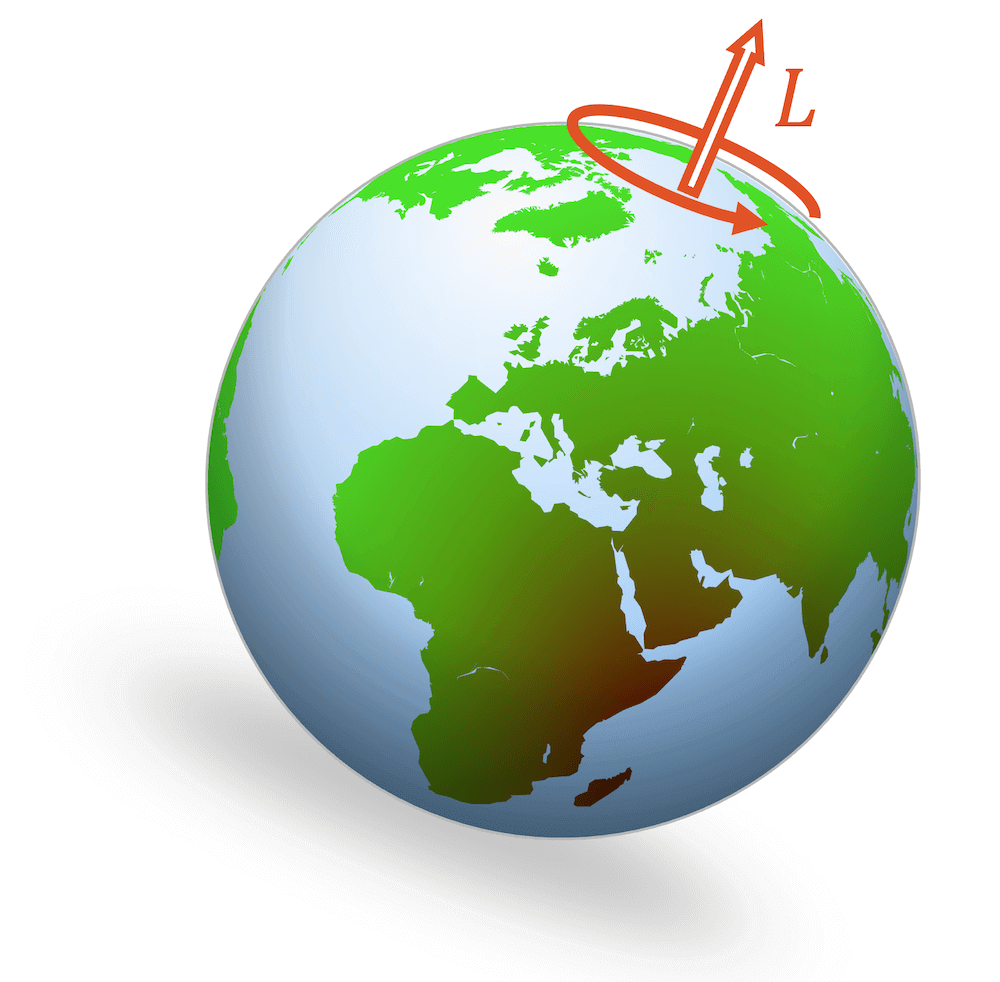
Die Erde macht auch eine Pirouette! Sie dreht sich um ihre eigene Achse und das schon seit ihrer Entstehung – Dank der Drehimpulserhaltung. Die exakte Periode der Erdrotation beträgt heute 23 h 56 min 4.10 s. Man schätzt aber, dass die Erde bei ihrer Entstehung vor rund 4 Milliarden Jahren eine Periode von nur 14 h hatte. Sie drehte schneller. Gewisse Reibungseffekte, v.a. aber die Gezeiten sind dafür verantwortlich, dass immer ein bisschen Drehimpuls abgegeben wird und die Tage länger werden.
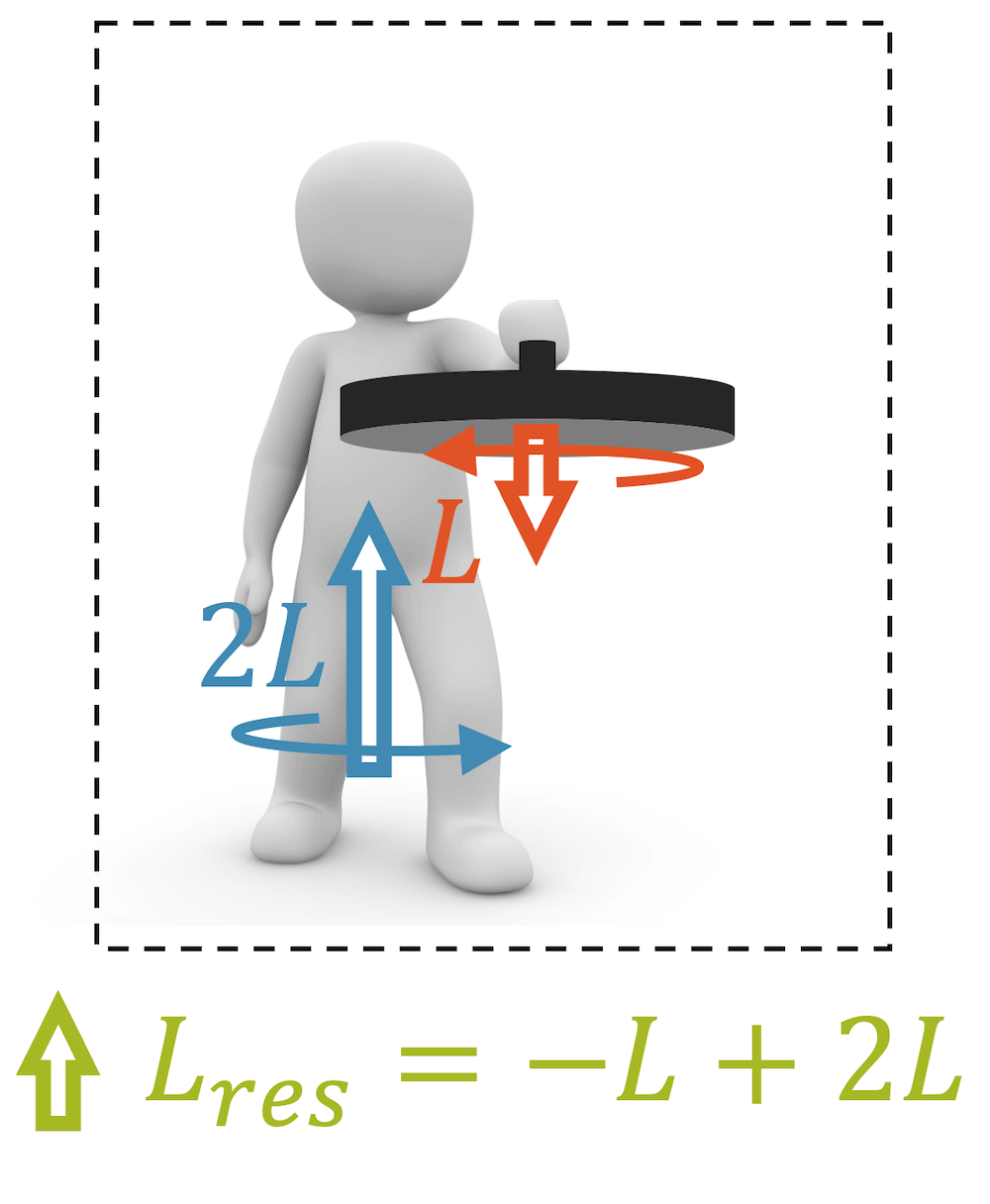
Die Erhaltung des Drehimpulses kann mit einem Experiment schön gezeigt werden: Im Bild hält das Männchen ein schnell rotierendes Rad mit dem Drehimpuls \(L\), der nach oben zeigt. Das Männchen selbst, dreht sich nicht. Der Drehimpuls des Systems “Männchen + Rad” hat in Summe den Drehimpuls vom Betrag \(L\) und mit der Richtung “nach oben”.

Wenn das Männchen das rotierende Rad umdreht, es aber weiterhin rotieren lässt, dann ändert der Drehimpuls des Rads seine Richtung. Stellen wir das Männchen auf eine rotierende Unterlage, so kann die Reibung am Boden keinen Drehimpuls dem System zuführen oder von ihm abführen. Der Drehimpuls muss aber erhalten bleiben und zwar \(L\) im Betrag und mit der Richtung “nach oben.”. Um dies zu gewährleisten, dreht sich das Männchen von selbst mit dem Drehimpuls \(2L\) nach oben. So beträgt die Summe der beiden Drehimpulse von Männchen und Rad wieder \(L\) “nach oben” und die Drehimpulserhaltung ist erfüllt.
Zylinder auf der schiefen Ebene
Warum rollt ein runder Bleistift auf einem Tisch, der nicht ganz waagrecht ist? Jeder und jede kennt das Phänomen, aber wie erklären wir die Physik dahinter. Es ist gar nicht so einfach, wenn man es wirklich genau erklären will.
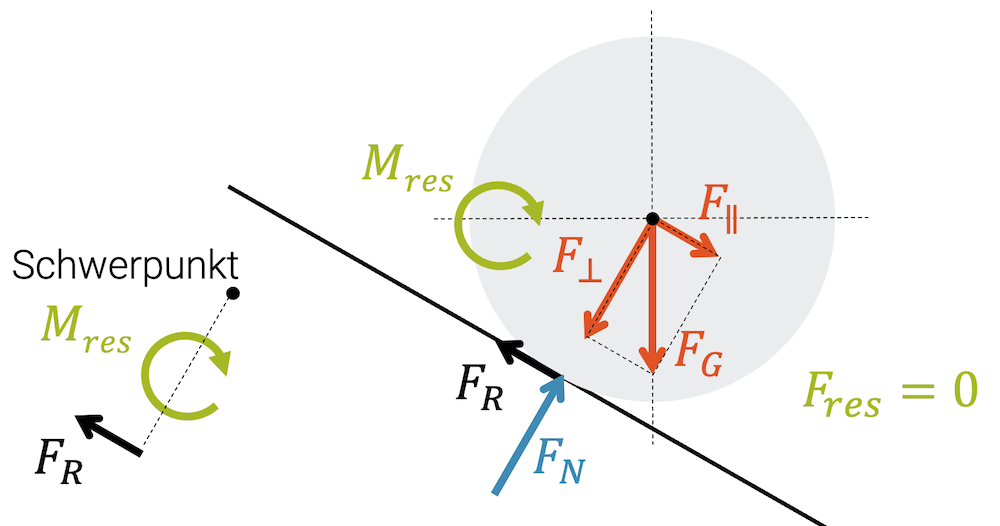
Den Bleistift können wir als Zylinder approximieren. An ihm wirkt die Gewichtskraft und zwar an seinem Schwerpunkt. Da die Unterlage nicht ganz horizontal ist, die Gewichtskraft aber streng vertikal wirkt, besteht die Gewichtskraft aus zwei Komponenten: Die grössere Komponente zeigt senkrecht zur Grundlage. Wir benutzen deshalb das Symbol für Senkrecht “\(\perp\)”. Die zweite Komponente wirkt parallel zur schiefen Unterlage und wird deshalb mit dem Symbol für Parallel bezeichnet: “\(\parallel\)”. Wir haben somit die Gewichtskraft aufgeteilt in eine Senkrechtkomponente \(F_{\perp}\) und eine Parallelkomponente \(F_{\parallel}\). Beide Teilkräfte addiert ergeben die Gewichtskraft:
\[ \vec{F}_G = \vec{F}_{\perp} + \vec{F}_{\parallel} \]
Wären das die einzigen Kräfte, so müsste der Zylinder, gemäss Newtons Zweitem Gesetz nach unten beschleunigt werden, d.h. in den Boden versinken. Das tut unser Bleistift natürlich nicht.
Die Oberfläche wirkt auf den Zylinder mit einer Normalkraft \(F_N\), die genau so gross ist, dass die gegen die Oberfläche wirkende Senkrechtkomponente \(F_{\perp}\) aufgehoben wird.
Was ist mit der Parallelkomponente? Wird diese auch aufgehoben? Wenn nicht, dann müsste Der Bleistift entlang der Oberfläche hinunter gleiten. Das würde er tatsächlich tun, wenn die Oberfläche ideal glatt wäre. Die meisten Oberflächen sind aber ein bisschen rauh und wir beobachten kein Gleiten, sondern eher ein Rollen des Bleistifts. Die Parallelkomponente \(F_{\parallel}\) wird ebenfalls neutralisiert, nämlich durch die Haftreibungskraft \(F_R\). Diese ist genau gleich gross im Betrag, jedoch umgekehrt in der Richtung zur Parallelkomponente \(F_{\parallel}\) und hebt diese auf.
Wir sehen damit, dass die Gewichtskraft durch die Normalkraft und die Haftreibungskraft aufgehoben wird. Aus Sicht der Kräfte haben wir Kräftegleichgewicht und der Bleistift müsste eigentlich an Ort und Stelle bleiben, denn die resultierende Kraft ist null:
\[ F_{res}=0 \]
Das Rollen des Bleistifts können wir damit noch nicht erklären. In der Statik haben wir aber nicht nur das Kräftegleichgewicht, sondern auch das Drehmomentgleichgewicht angeschaut. Wie steht es mit dem?
Wir wählen den Schwerpunkt als unseren Betrachtungspunkt und suchen alle Drehmomente bezüglich diesem Punkt. Alle Kräfte haben Wirkungslinien, die durch den Schwerpunkt gehen, d.h. sie haben somit keinen Abstand zum Schwerpunkt und haben kein Drehmoment bezüglich diesem Punkt. Einzig die Haftreibungskraft hat eine Wirkungslinie, die einen Abstand zum Schwerpunkt hat. Sie erzeugt ein Drehmoment im Uhrzeigersinn. Das resultierende Drehmoment ist wegen der Haftreibungskraft nicht null:
\[ M_{res}>0 \]
Dieses Drehmoment wird den Drehimpuls unseres Zylinders verändern und den Bleistift zum Rollen bringen. Wir erinnern uns: Eine ideal glatte Oberfläche macht, dass der Bleistift nach unten rutscht, ohne zu rollen. Die Haftreibung ist für das Rollen verantwortlich.
Jetzt überlegen wir uns, wie der Drehimpuls in den Bleistift kommt. Wirkt ein resultierendes Drehmoment eine gewisse Zeit \(\Delta t\) lang auf einen Körper, so ändert sich der Drehimpuls von ihm: \(\Delta L\).
\[ M_{res}=\frac{\Delta L}{\Delta t} \quad \quad \rightarrow \quad \quad \Delta L = M_{res} \cdot \Delta t \]
Beim Zylinder haben wir einen starren Körper mit einem konstanten Trägheitsmoment \(I\), d.h. der Drehimpuls kann sich nur über die Winkelgeschwindigkeit \(\omega\) ändern. Das resultierende Drehmoment hat somit eine direkte Wirkung auf die Winkelgeschwindigkeit:
\[ \Delta L = I \cdot \Delta \omega \quad \quad \rightarrow \quad \quad \Delta \omega = \frac{\Delta L}{I} = \frac{M_{res} \cdot \Delta t}{I} \]
Die Winkelgeschwindigkeit nimmt umso stärker zu, je grösser das resultierende Drehmoment, je länger die Wirkzeit ist und je kleiner das Trägheitsmoment ist. Wir sehen, dass das Trägheitsmoment seinem Namen alle Ehre macht. Ist das Trägheitsmoment gross, nimmt die Winkelgeschwindigkeit weniger stark zu, da das System tatsächlich träger ist.
Wenn wir also zwei Zylinder haben, die exakt die gleichen Abmessungen haben und exakt die gleiche Masse, dann sind sie von aussen nicht zu unterscheiden. Ist jeder der eine hohl und aus einem schweren Material, d.h. mit viel Masse weit weg von der Drehachse, so ist sein Trägheitsmoment gross. Ein voller Zylinder hat im Vergleich ein kleineres Trägheitsmoment.
Wenn wir die Tabelle der Trägheitsmomente konsultieren, so kommen wir auf \(I=\frac{1}{2}mr^2\) für den vollen Zylinder und auf \(I=mr^2\) für den hohlen Zylinder. Letzterer hat ein doppelt so grosses Trägheitsmoment.
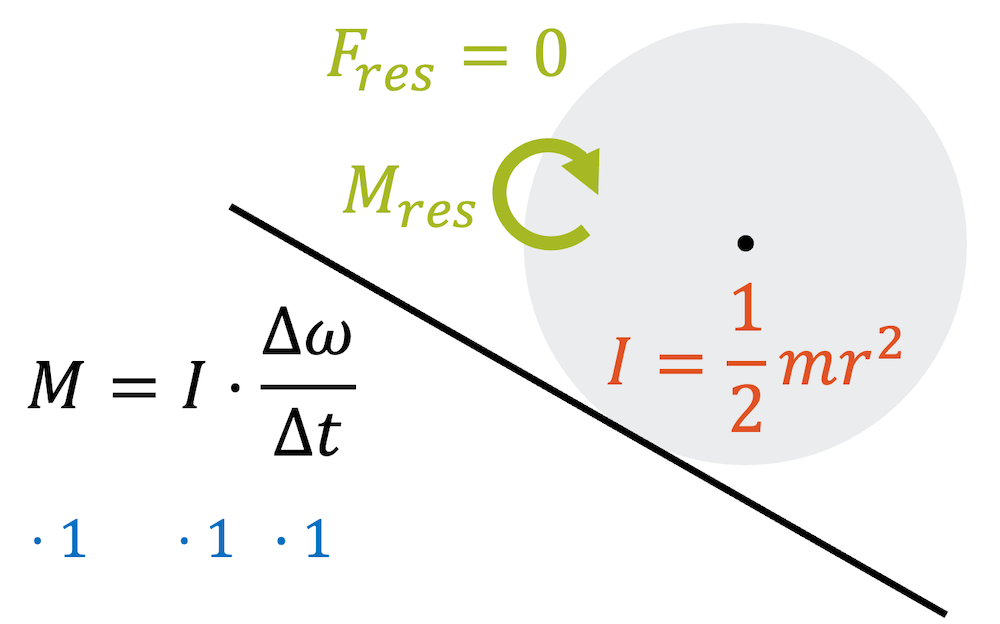
Angetrieben werden beide durch das gleiche Drehmoment \(M_{res}\), das von der Gewichtskraft und dem Neigungswinkel abhängig ist. Wenn wir also das gleiche Antriebsmoment haben, der eine aber doppelt so träge ist, wie der andere, wird der volle Zylinder doppelt so schnell drehen und somit schneller starten, als der hohle Zylinder.
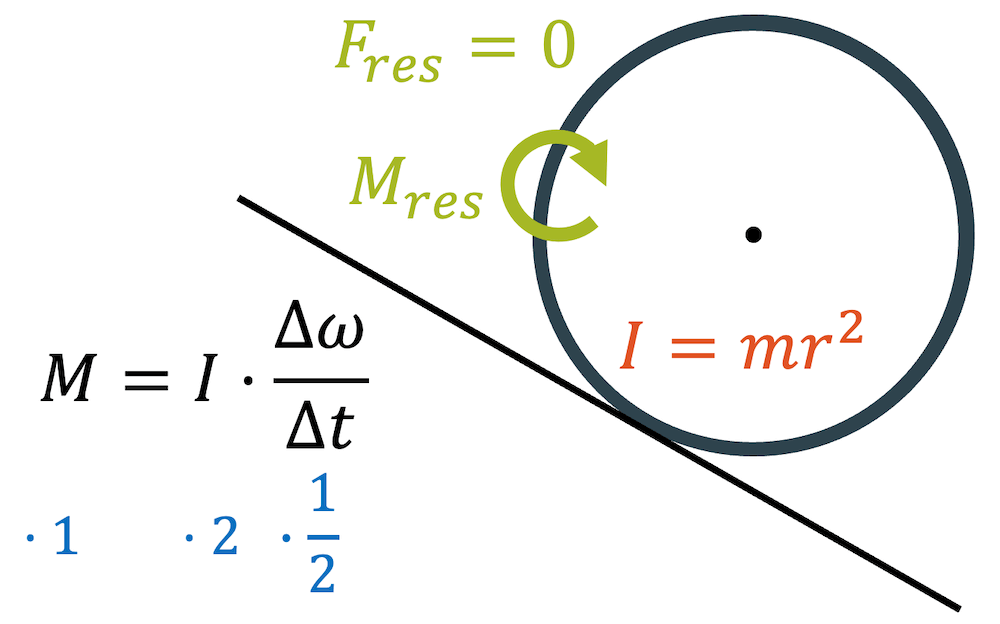
Aufgabensammlung
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt








Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.